Вариант № 5
Код 5, 15, 25, 35, 45, 55, 65, 75
Задание 5
Найти область определения функции
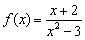
Решение: в числителе ничего особенного нет, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти «плохие» точки:
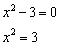
Полученное уравнение имеет два корня: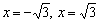 
. Данные значения не входят в область определения функции. Действительно, подставьте 
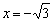или 
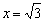в функцию 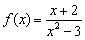и вы увидите, что знаменатель обращается в ноль.
Ответ: область определения: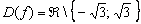 
Задание 15
Найти предел функции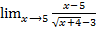 
= 
= 
= 
= 
= 
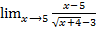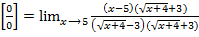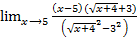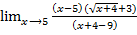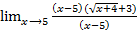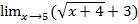=3+3=6
Задание 25
Дано: прямоугольный параллелепипед ABCDA1B1C1D1; DA=1; DC=2; DD1=3. Найти: угол между прямыми CB1 и D1B.
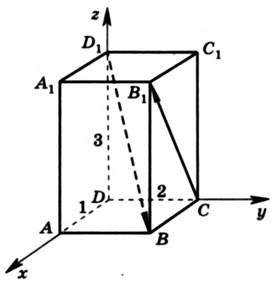
Рис. 1.
Решение
Введем систему координат Dxyz (см. рис. 1) и найдем направляющие векторы D1B и СB1. Для этого сначала найдем координаты точек D1, B, C и B1, так как через них проходят нужные нам прямые. D1(0;0;3), B(1;2;0), C(0;2;0), B1(1;2;3). Зная координаты точек, мы можем найти координаты направляющих векторов, вычитая из координат конца координаты начала вектора: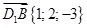 
, 
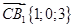. Найдем косинус угла между прямыми CB1 и D1B: 
.
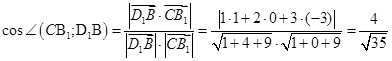Значит,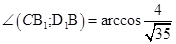 
.
Задание 35
Найти производную функции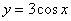 
Решение
Смотрим в таблицу производных. Производная косинуса там есть, но у нас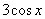 
.
Решаем:
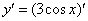
Самое время использовать правило, выносим постоянный множитель за знак производной:
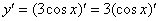
А теперь превращаем наш косинус по таблице:
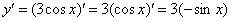
Ну и результат желательно немного «причесать» – ставим минус на первое место, заодно избавляясь от скобок:
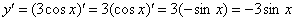
Задание 45
Исследовать функцию и построить график функции
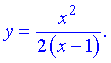
Решение:
1) Функция определена везде кроме точки, в которой знаменатель превращается в ноль (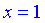 
). Область определения состоит из двух интервалов
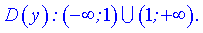
2) При подстановке значения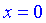 
получим
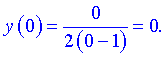
Такую же точку получим если приравняем функцию к нулю. Точка 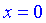- единственная точка пересечения с осями координат.
3) Проверяем функцию на четность
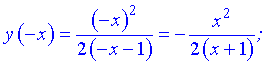
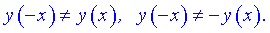
Итак функция ни четная, ни нечетная, непериодическая.
4) В данном случае имеем одну точку разрыва 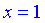. Вычислим границы слева и справа от этой точки
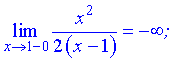
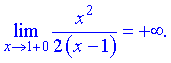
Итак 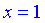– точка разрыва второго рода.
5) Для отыскания интервалов монотонности вычисляем первую производную функции
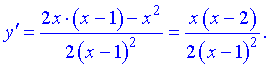
Приравнивая ее к нулю получим точки подозрительные на экстремум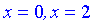 
. Они разбивают область определения на следующие интервалы монотонности
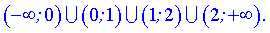
Исследуем поведение производной слева и справа от найденных точек разбиения
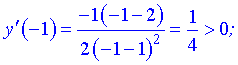
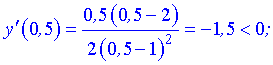
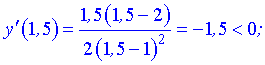
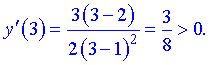
Графически интервалы монотонности будут иметь вид
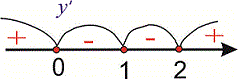
Исследуемая функция возрастает на интервалах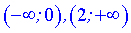 
и убывает 
.
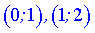Точка 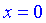– точка локального максимума, 
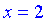– локального минимума. Найдем значение функции
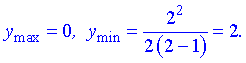
6) Для отыскания интервалов выпуклости найдем вторую производную
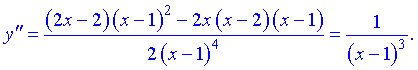
Таких интервалов нет, поскольку вторая производная не принимает нулевых значений в области определения.
7) Точка 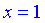– вертикальная асимптота функции. Уравнение наклонной асимптоты имеет вид
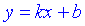
где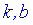 
- границы которые вычисляются по правилу
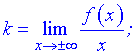
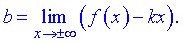
Находим нужные границы
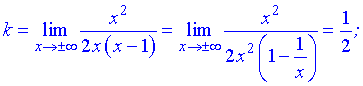
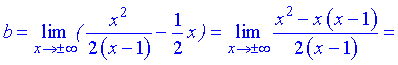
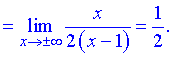
Конечный вид прямой следующий
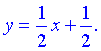
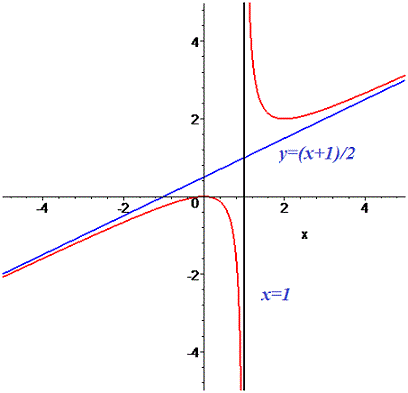
8) На основе проведенного анализа выполняем построение графика функции. Для этого сначала строим вертикальные и наклонные асимптоты, затем находим значение функции в нескольких точках и по них проводим построение.
--------------------------------------
Задание 55
Вычислить определённый интеграл
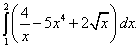
Используя свойства определённого интеграла, а при нахождении первообразных – табличные интегралы получим
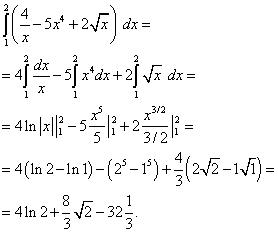
Задание 65
Найти площадь фигуры, ограниченной линиями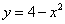 
, 
, 
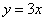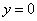и находящейся в 1-й четверти.
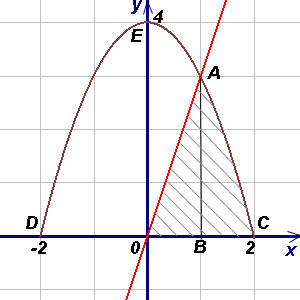
Решение
Чтобы воспользоваться формулой (1), представим площадь искомой фигуры в виде суммы площадей треугольника OAB и криволинейной трапеции ABC. При вычислении площади треугольника OAB пределами интегрирования служат абсциссы точек O и A, а для фигуры ABC - абсциссы точек A и C (A является точкой пересечения прямой OA и параболы, а C - точкой пересечения параболы с осью Ox). Решая совместно (как систему) уравнения прямой и параболы, получим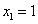 
(абсциссу точки A) и 
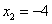(абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично получим 
, 
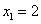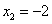(абсциссы точек C и D). Таким образом имеем всё для нахождения площади фигуры. Находим:
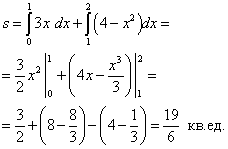
Задание 75
Конференция длится три дня. В первый и второй день выступают по 15 докладчиков, в третий день – 20. Какова вероятность того, что доклад профессора Морозова выпадет на третий день, если порядок докладов определяется жеребьевкой?
Решение
Что здесь является элементарным исходом? – Присвоение докладу профессора какого-то одного из всех возможных порядковых номеров для выступления. В жеребьевке участвует 15+15+20=50 человек. Таким образом, доклад профессора Морозова может получить один из 50 номеров. Значит, и элементарных исходов всего 50.
А какие исходы благоприятные? – Те, при которых окажется, что профессор будет выступать в третий день. То есть, последние 20 номеров.
По формуле вероятность P(A)= 20/50=2/5=4/10=0,4
Ответ: 0,4
Дата: 2019-11-01, просмотров: 267.
