МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
по организации самостоятельной работы
студентов заочного отделения
ЕН.01Математика
по специальности 21.02.17
«Подземная разработка месторождений полезных ископаемых»
Разработал преподаватель Левченко В.А.
2019
Методические рекомендации предназначены для организации самостоятельной работы студентов заочного отделения специальности 21.02.17 «Подземная разработка месторождений полезных ископаемых» на основе среднего образования на основе образовательно-квалифицированного уровня квалифицированного рабочего по дисциплине ЕН.01 Математика.
Содержание
| Пояснительная записка | 4 |
| Тематический план для специальности 21.02.17 на основе среднего образования | 5 |
| Тематический план для специальности 21.02.17 на основе образовательно-квалифицированного уровня квалифицированного рабочего | 6 |
| Содержание программы и рекомендации к её самостоятельному изучению | 7 |
| Перечень и содержание практических занятий | 17 |
| Методические рекомендации по выполнению и оформлению домашней контрольной работы | 62 |
| Таблица вариантов с кодами заданий для специальности 21.02.17 на основе среднего образования | 63 |
| Таблица вариантов с кодами заданий для специальности 21.02.17 на основе образовательно-квалифицированного уровня квалифицированного рабочего | 64 |
| Образец выполнения домашней контрольной работы | 74 |
| Критерии оценивания выполнения домашней работы | 81 |
| Перечень экзаменационных вопросов | 82 |
| Критерии оценивания знаний по дисциплине | 84 |
| Литература | 85 |
1. Пояснительная записка
Программа учебной дисциплины ЕН.01 Математика предназначена для изучения в образовательных учреждениях среднего профессионального образования, при подготовке специалистов среднего звена.
Дисциплина ЕН.01 Математика относится к дисциплинам математического и естественнонаучного цикла подготовки специалистов среднего звена.
Для студентов специальности 21.02.17 «Подземная разработка месторождений полезных ископаемых» на основе среднего образования на освоение учебной дисциплины отведено 94 часа.
Для студентов специальности 21.02.17 «Подземная разработка меторождений полезных ископаемых» на образовательно-квалифицированного уровня квалифицированного рабочего на освоение учебной дисциплины отведено 72 часа.
В результате изучения учебной дисциплины студенты должны:
уметь:
- решать прикладные задачи в области профессиональной деятельности;
знать:
- значение математики в профессиональной деятельности и при освоении профессиональной подготовки специалистов среднего звена;
- основные математические методы решения прикладных задач в области профессиональной деятельности;
основные понятия и методы:
- математического анализа;
- линейной алгебры;
- теории комплексных чисел;
- теории вероятностей и математической статистики;
- основы интегрального и дифференциального исчисления.
Содержание дисциплины должно быть ориентировано на использовании и применении математического аппарата в специальных дисциплинах, подготовки курсовых и расчётных работ.
Базовыми дисциплинами для изучения дисциплины ЕН.01 Математика являются учебные дисциплины «Алгебра и начала математического анализа», «Геометрия».
В методических рекомендациях по изучению учебной дисциплины ЕН.01Математика приведены тематические учебные планы для специальности 21.02.17 «Подземная разработка месторождений полезных ископаемых» на основе среднего образования и на основе образовательно-квалифицированного уровня квалифицированного рабочего.
ТЕМАТИЧЕСКИЙ ПЛАН
учебной дисциплины ЕН.01 Математика
для заочной формы обучения
специальности 21.02.17
«Подземная разработка месторождений полезных ископаемых»
на основе среднего образования
| № п/п |
Наименование раздела и темы
Количество часов
всего по учебному плану
Аудитор.
Занятий
В том числе
самост.
Работа
Итого:
ТЕМАТИЧЕСКИЙ ПЛАН
учебной дисциплины ЕН.01 Математика
для заочной формы обучения
специальности 21.02.17
«Подземная разработка месторождений полезных ископаемых»
на основе образовательно-квалифицированного уровня
квалифицированного рабочего
| № п/п |
Наименование раздела и темы
Количество часов
всего по учебному плану
Аудитор.
Занятий
В том числе
самост.
Работа
Итого:
3. Содержание программы и рекомендации к её самостоятельному изучению
Раздел 2. Комплексные числа
Тема 4.1 Предел функции
Понятие бесконечной числовой последовательности. Возрастающие и убывающие числовые последовательности. Бесконечно малые и бесконечно большие величины. Связь бесконечно малой величины с бесконечно большой. Предел последовательности. Ограниченные величины. Основные теоремы о пределах. Свойства пределов. Признаки существования пределов. Неопределённости, виды неопределённостей. Предел функции. Число е. Натуральные логарифмы. Вычисление пределов функции. Два замечательных предела.
Практическое занятие. Вычисление пределов
Вопросы для самопроверки:
1. Какая последовательность называется числовой последовательностью?
2. Каким может быть характер изменение переменной величины?
3. Какому условию должна удовлетворять ограниченная переменная величина?
4. Приведите примеры ограниченных переменных величин.
5. Дайте определение бесконечно малой величины.
6. Дайте определение бесконечно большой величины.
7. Какая связь существует между бесконечно малой и бесконечно большой величинами?
8. Перечислите основные свойства бесконечно малых.
9. Перечислите теоремы о пределах и следствия из них.
10. Перечислите теоремы и следствия из них, на которых основано вычисление предела функции.
11. Что представляет собой число е?
12. Что называется приращением аргумента и приращением функции?
13. Какие два предела называются замечательными?
14. Какие виды неопределённостей вам известны?
15. Назовите основные теоремы о пределах?
Раздел. 6
Решение заданий
Задание 1.
Пусть
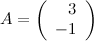 .
.
Найти матрицу
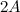 .
.
Решение.
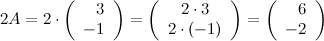
Ответ.
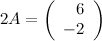
Задание 2.
Найти
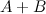 , если
, если
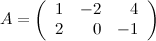 ,
, 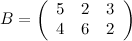
Решение.
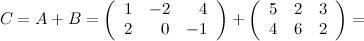
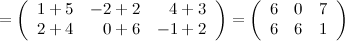
Ответ
. 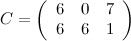
Задание 3. Найти матрицу 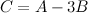 ,
,
если 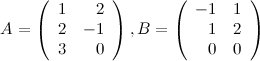
Решение. 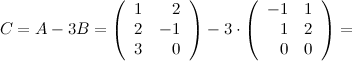
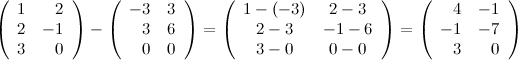
Ответ.
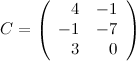
Задание 4. Вычислить 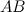 и
и 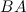 ,
,
если
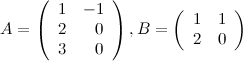
Решение. Так как 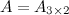 , а
, а 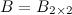 , то произведение возможно и результатом операции умножения будет матрица
, то произведение возможно и результатом операции умножения будет матрица 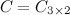 , а это матрица вида
, а это матрица вида 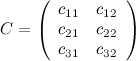 .
.
Вычислим элементы матрицы 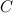 :
:
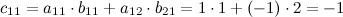
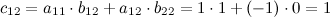
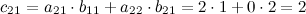
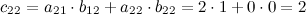
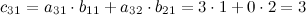
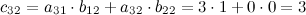
Итак, 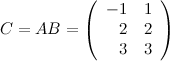 .
.
Выполним произведения в более компактном виде:
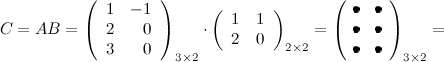
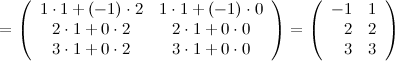
Найдем теперь произведение 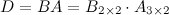 . Так как количество столбцов матрицы
. Так как количество столбцов матрицы 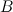 (первый сомножитель) не совпадает с количеством строк матрицы
(первый сомножитель) не совпадает с количеством строк матрицы 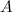 (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
(второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. 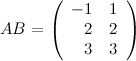 . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы
. В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы 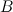 не совпадает с количеством строк матрицы
не совпадает с количеством строк матрицы 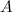 .
.
Задание 5. Найти матрицу 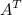 , если
, если
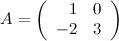
Решение.
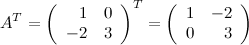
Ответ.
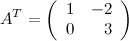
Задание 6. Найти минор 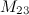 к элементу
к элементу 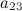 определителя
определителя
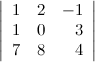 .
.
Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
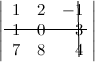
тогда
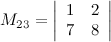
Ответ.
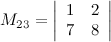
Задание 7. Найти алгебраическое дополнение 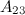 к элементу
к элементу 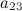 определителя
определителя
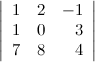 .
.
Решение.
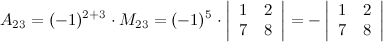
Ответ.
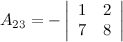
Задание 8. Вычислить определитель матрицы.
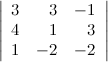
Решение.
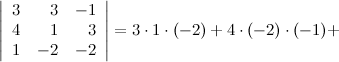
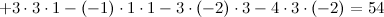
Ответ.
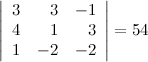
Задание 9. Найти обратную матрицу к матрице
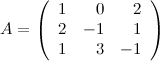
Решение. Вычисляем определитель матрицы:
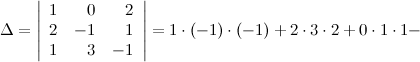
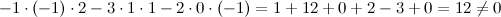
Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица 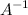 к матрице
к матрице 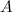 находится по формуле:
находится по формуле:
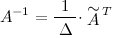
Найдем союзную матрицу 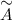 , для этого вычислим алгебраические дополнения к элементам матрицы
, для этого вычислим алгебраические дополнения к элементам матрицы 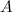 :
:
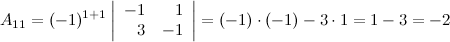
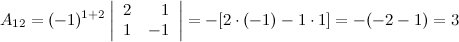
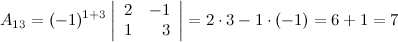
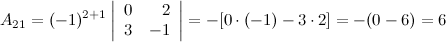
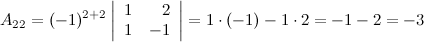
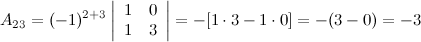
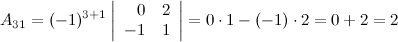
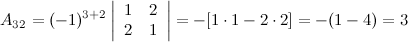
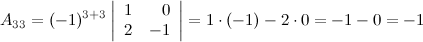
Таким образом, 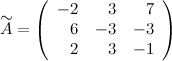
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
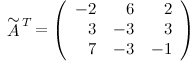
Итак,
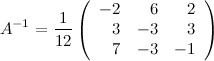
Ответ.
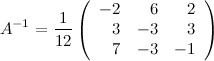
Практическое занятие. Решение систем линейных уравнений.
Цель. Формировать умение исследовать и использовать различные методы для решения систем линейных алгебраических уравнений.
Решение задач
Справочный материал и примеры.
Рассмотрим системы линейных алгебраических уравнений (СЛАУ) произвольной размерности, состоящие из m уравнений с n неизвестными:
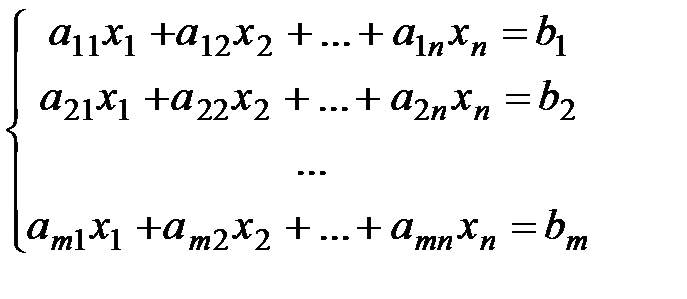 . (*)
. (*)
Матрица 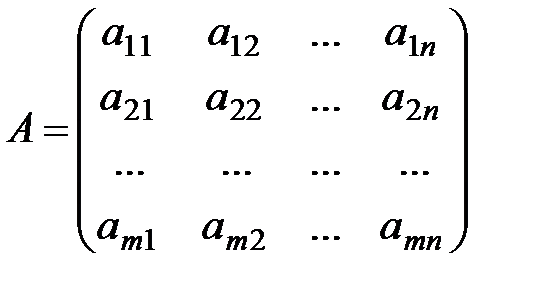 , составленная из коэффициентов системы (*), называется матрицей системы (ее размер – mxn), а вектор
, составленная из коэффициентов системы (*), называется матрицей системы (ее размер – mxn), а вектор 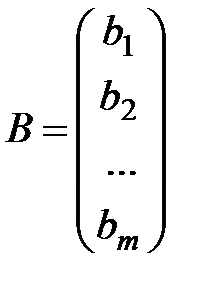 (m-мерный)- столбцом (вектором) свободных членов. Матрицу вида
(m-мерный)- столбцом (вектором) свободных членов. Матрицу вида 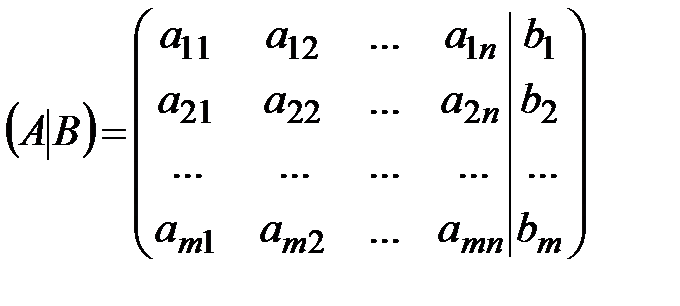 называют расширенной матрицей системы (*). Любой набор значений неизвестных
называют расширенной матрицей системы (*). Любой набор значений неизвестных 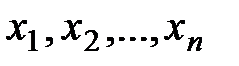 , образующих n-мерный вектор
, образующих n-мерный вектор 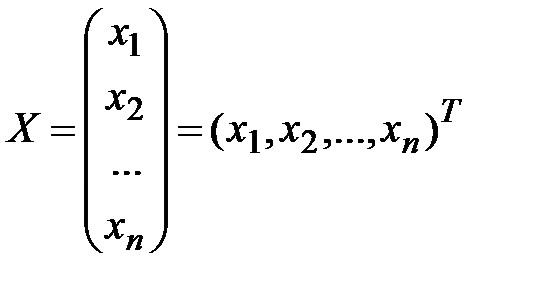 , является решением системы (*), если эти числа удовлетворяют всем уравнениям системы (т.е. превращают их в тождества). Очевидно, что
, является решением системы (*), если эти числа удовлетворяют всем уравнениям системы (т.е. превращают их в тождества). Очевидно, что 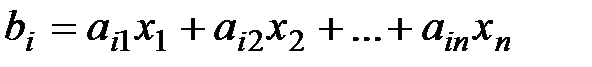 при каждом i=1,2,…,m (i-е уравнение представляет собой скалярное произведение i-й строки матрицы системы на вектор X), и (*) можно переписать в виде
при каждом i=1,2,…,m (i-е уравнение представляет собой скалярное произведение i-й строки матрицы системы на вектор X), и (*) можно переписать в виде
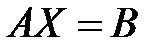 . (**)
. (**)
Запись (**) называется "матричной (векторной) формой записи" системы (*).
Пример 1. Выписать матрицу коэффициентов и столбец свободных членов для СЛАУ 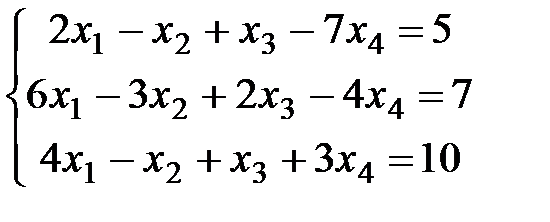 .
.
Решение. Очевидно, что 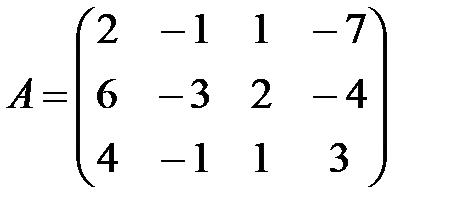 ;
; 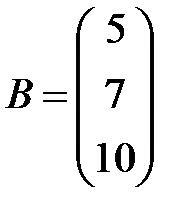 .
.
Пример 2. Записать СЛАУ, если 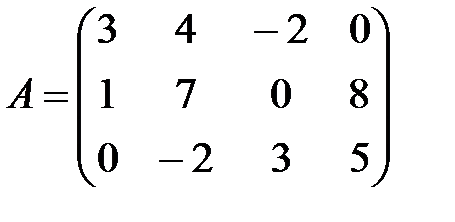 ,
, 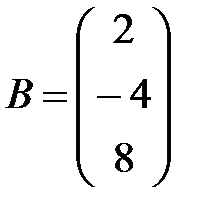 .
.
Решение. Введем в рассмотрение вектор X и с каждым столбцом мысленно сопоставим неизвестное: с первым столбцом - 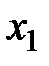 , со вторым -
, со вторым - 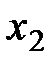 , с третьим -
, с третьим - 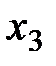 , с четвертым -
, с четвертым - 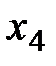 . Окончательно нужная система линейных алгебраических уравнений имеет вид
. Окончательно нужная система линейных алгебраических уравнений имеет вид
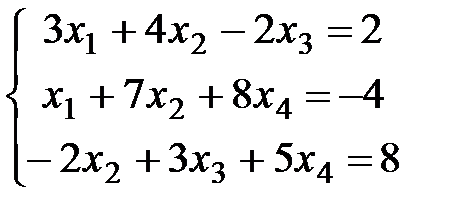 .
.
Классификация систем линейных алгебраических уравнений. Определения и основные теоремы. Если СЛАУ (*) имеет, хотя бы одно решение, она называется совместной (соответственно, система несовместная, если она вообще не имеет решений). Совместная система (*) называется определенной, если она имеет единственное решение, и неопределенной, если имеет более одного решения (в последнем случае у нее бесконечно много решений).
Матрицу системы (*) будем называть приведенной (а саму систему канонической), если в каждой i-й строке (i=1,2,…,m) есть элемент 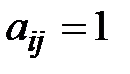 , а все остальные элементы j-го cтолбца равны нулю. Такие элементы (и соответствующие им неизвестные) будем называть ведущими, а оставшиеся неизвестные назовем свободными.
, а все остальные элементы j-го cтолбца равны нулю. Такие элементы (и соответствующие им неизвестные) будем называть ведущими, а оставшиеся неизвестные назовем свободными.
Теорема 1 (Кронекера-Капелли). СЛАУ (*) совместна тогда и только тогда, когда ранг матрицы системы совпадает с рангом ее расширенной матрицы, т.е выполняется равенство 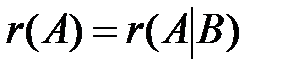 .
.
Для совместной системы число 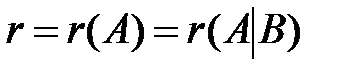 назовем рангом системы.
назовем рангом системы.
Теорема 2 (о количестве решений). Пусть СЛАУ (*) совместна. Если ее ранг равен числу неизвестных ( 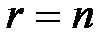 ), то система является определенной; если ранг системы меньше числа неизвестных (
), то система является определенной; если ранг системы меньше числа неизвестных ( 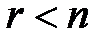 ), то исходная система – неопределенная.
), то исходная система – неопределенная.
Неопределенная система, как было отмечено, имеет бесконечное множество решений. Совокупность всех решений называется общим решением системы.
Алгоритм метода Гаусса. Цель рассуждений – путем элементарных преобразований свести исходную систему к равносильной, решение которой можно выписать непосредственно. Основными шагами метода Гаусса являются следующие.
I. Прямой ход. Выписать расширенную матрицу системы, путем элементарных преобразований свести ее к эквивалентной ступенчатой и определить ранги матрицы и расширенной матрицы системы. Если они различны, то исходная система несовместна, т.е. не имеет решений. Если 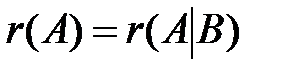 , то переходим к следующему этапу.
, то переходим к следующему этапу.
II. Сравнить ранг системы и число неизвестных, сделать вывод о количестве решений, учитывая теорему 2.
III. Обратный ход. Ступенчатую матрицу преобразовать к эквивалентной ей приведенной. Определить, какие неизвестные являются ведущими, какие – свободными.
IV. Выписать по полученной матрице систему, записать ответ (выразив, в случае неопределенной системы, ведущие элементы через свободные для построения общего решения).
Пример 3. Решить СЛАУ 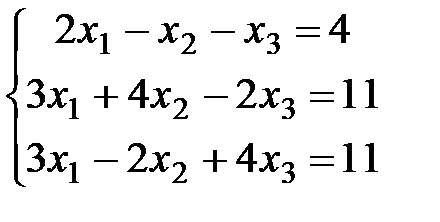 .
.
Решение. Преобразуем расширенную матрицу системы:
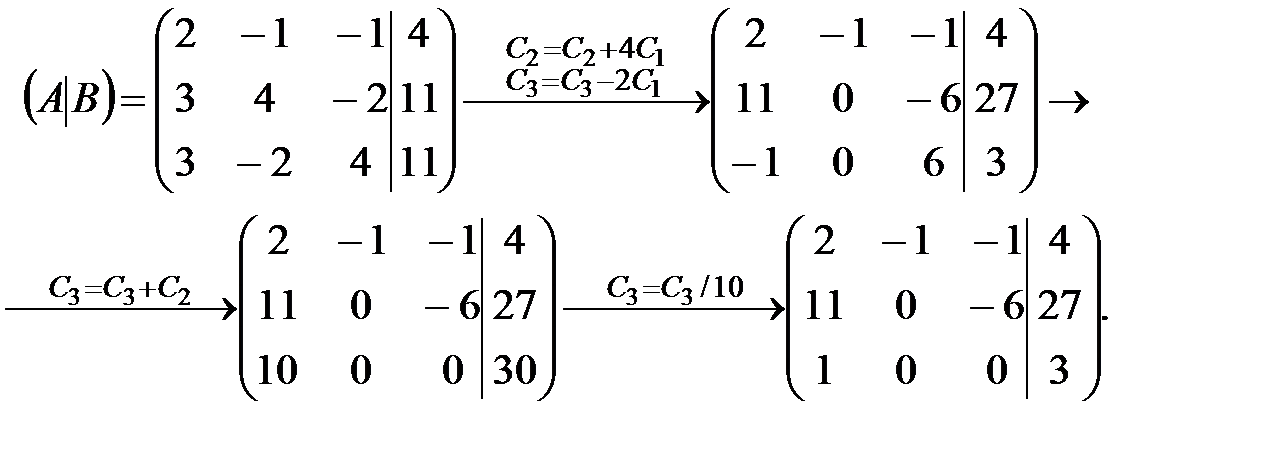
Последняя матрица – ступенчатая. Ведущими неизвестными для нее являются 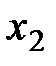 в первой строке,
в первой строке, 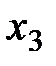 во второй и
во второй и 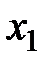 в третьей. Очевидно, что система совместна и ее ранг равен 3:
в третьей. Очевидно, что система совместна и ее ранг равен 3: 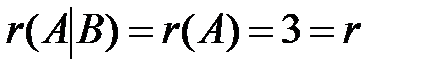 . Поскольку число неизвестных также равно 3, исходная система является определенной.
. Поскольку число неизвестных также равно 3, исходная система является определенной.
Переходим к проведению преобразований по обратному методу Гаусса (теперь необходимо получать нули НАД ведущими элементами).
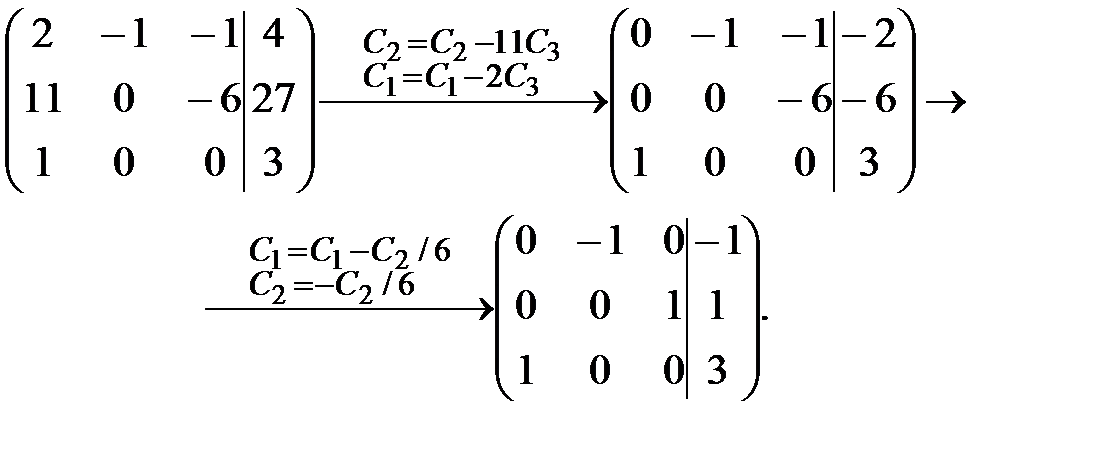
Теперь составляем по последней матрице систему 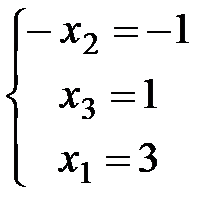 и выписываем значения неизвестных в порядке их номеров: X=(3;1;1)T. Это и есть ответ.
и выписываем значения неизвестных в порядке их номеров: X=(3;1;1)T. Это и есть ответ.
Пример 4. Для СЛАУ 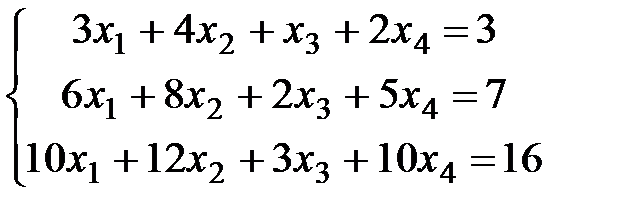 найти общее и два частных решения.
найти общее и два частных решения.
Решение. Приведем расширенную матрицу системы к ступенчатой.
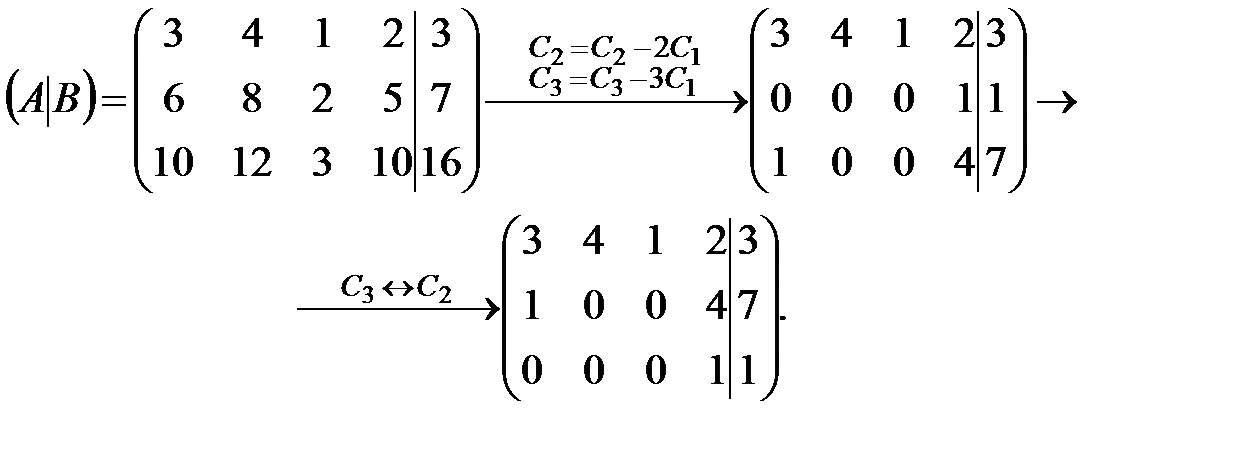
Очевидно, что 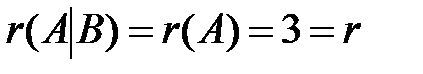 , число неизвестных n=4 и в соответствии с теоремой 6.2 исходная система является неопределенной. Ведущие неизвестные:
, число неизвестных n=4 и в соответствии с теоремой 6.2 исходная система является неопределенной. Ведущие неизвестные: 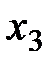 в первой строке,
в первой строке, 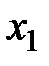 во второй,
во второй, 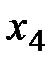 в третьей. Свободное неизвестное -
в третьей. Свободное неизвестное - 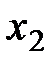 . Обратным ходом преобразуем матрицу к приведенному виду:
. Обратным ходом преобразуем матрицу к приведенному виду:
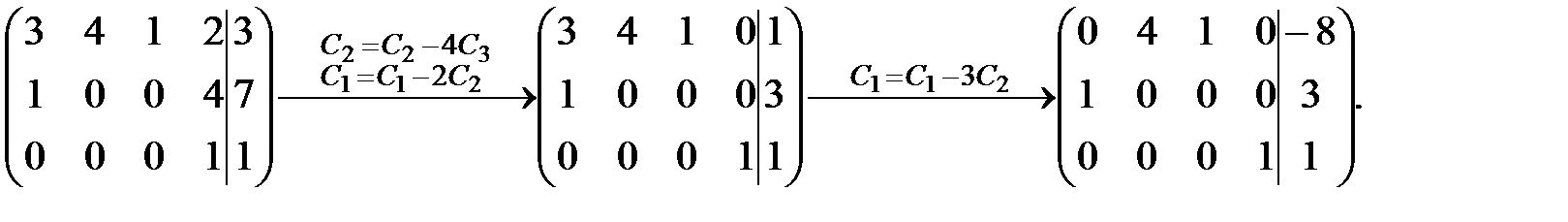
Выписываем полученную систему и ведущие неизвестные выражаем через свободные: 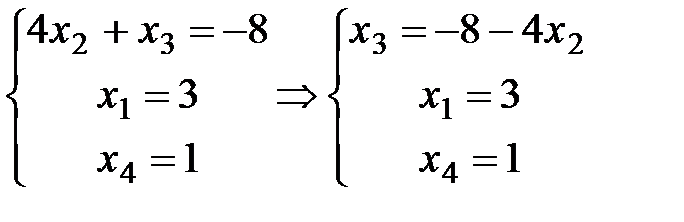 . Общее решение записываем в порядке нумерации неизвестных:
. Общее решение записываем в порядке нумерации неизвестных: 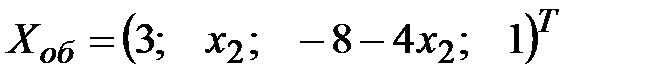 ,
, 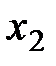 - любое вещественное число.
- любое вещественное число.
Частное решение можно получить, если придать свободному неизвестному 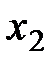 конкретное числовое значение. Например, при
конкретное числовое значение. Например, при 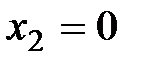
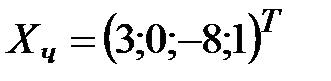 , а при
, а при 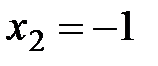
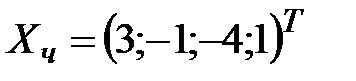 .
.
Теорема Крамера. Рассмотрим «квадратную» систему линейных уравнений (число неизвестных совпадает с числом уравнений) вида
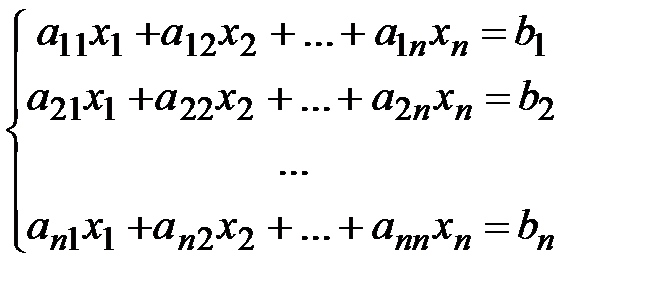 . (*)
. (*)
Теорема 3 (теорема Крамера). Если определитель матрицы системы (*) отличен от нуля ( 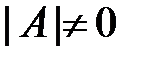 ), то данная система имеет единственное решение, причем значения неизвестных находятся по формулам
), то данная система имеет единственное решение, причем значения неизвестных находятся по формулам
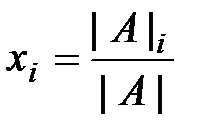 , i=1,2,…,n
, i=1,2,…,n
где 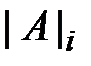 - определитель матрицы, полученной из исходной матрицы системы путем замены i-го столбца на столбец свободных членов.
- определитель матрицы, полученной из исходной матрицы системы путем замены i-го столбца на столбец свободных членов.
Пример 5. Решить систему 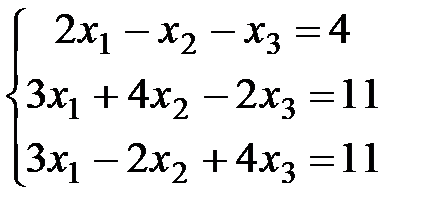 методом Крамера.
методом Крамера.
Решение. Выписываем A - матрицу системы и B - столбец свободных членов: 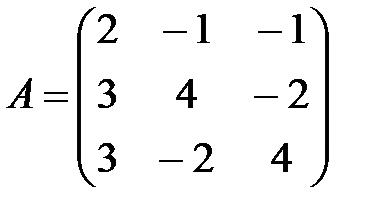 ,
, 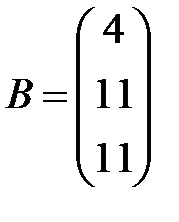 . Далее вычисляем определители:
. Далее вычисляем определители:
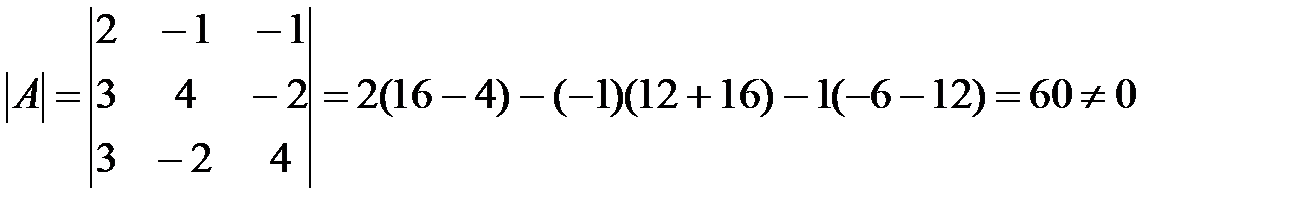 ;
;
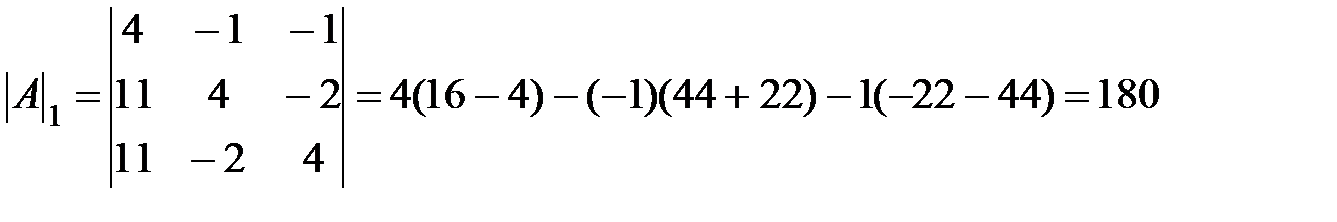 ;
;
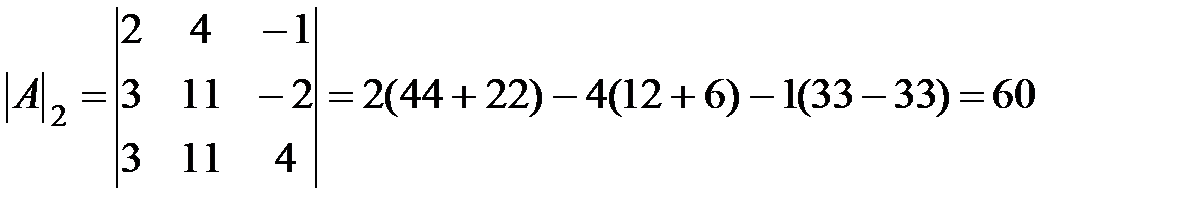 ;
;
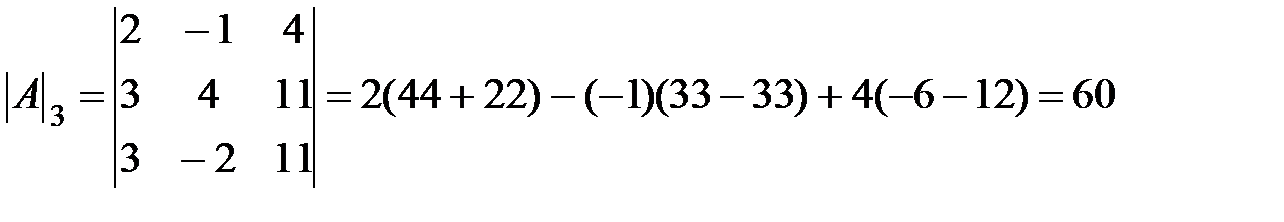 .
.
По теореме Крамера 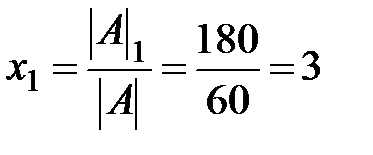 ;
; 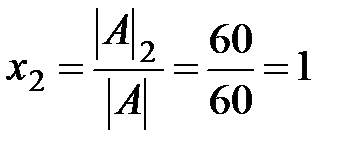 ;
; 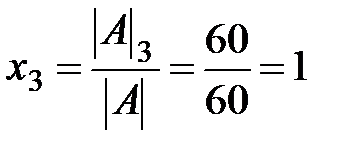 . Для проверки результата подставим полученные значения неизвестных в каждое уравнение системы:
. Для проверки результата подставим полученные значения неизвестных в каждое уравнение системы: 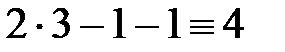 ,
, 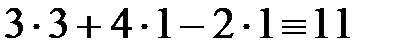 ,
, 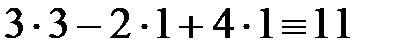 . Все уравнения обратились в тождества, значит, решение найдено верно.
. Все уравнения обратились в тождества, значит, решение найдено верно.
Задание 1. По расширенной матрице выписать СЛАУ.
1) 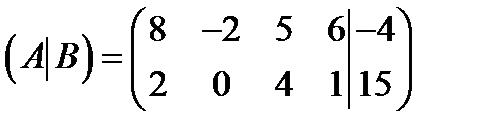
| 2) 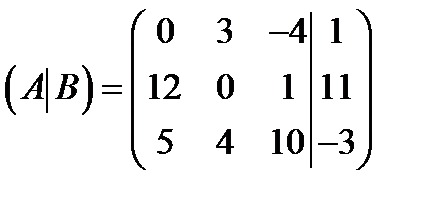
|
3) 
| 4) 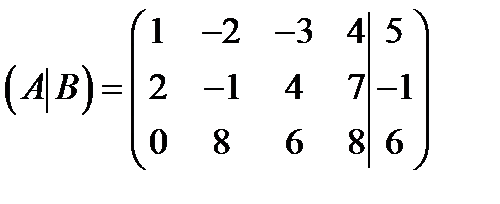
|
Задание 2. Решить системы уравнений методом Крамера и методом Гаусса.
1) 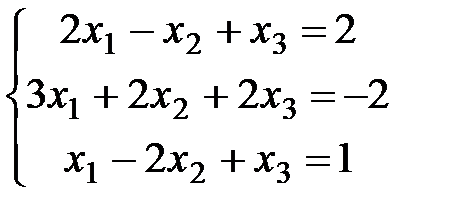
| 2) 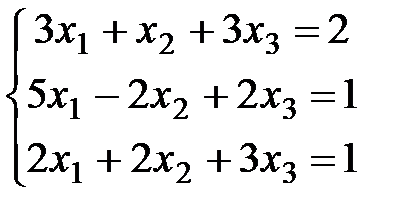
|
3) 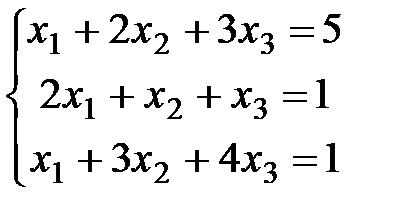
| 4) 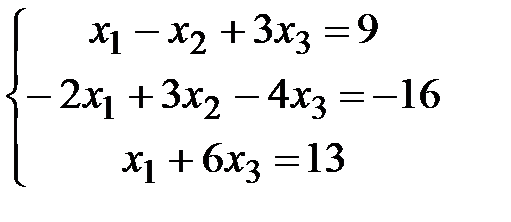
|
Задание 3. Решить СЛАУ (в случае неопределенной системы выписывать общее и два любых частных решения).
1) 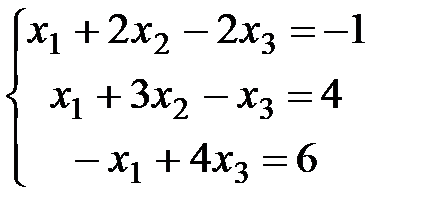
| 2) 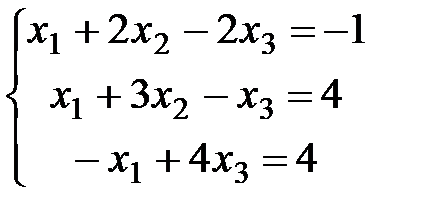
|
3) 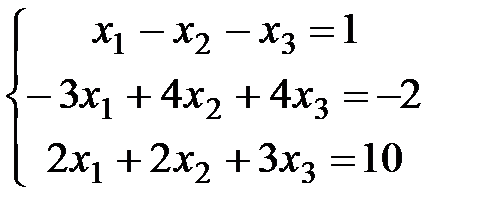
| 4) 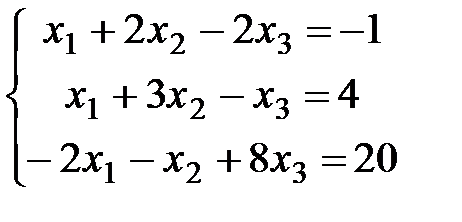
|
Практическое занятие. Операции над комплексными числами. Приложение комплексных чисел.
Цель.
Решение задач
Пример 1. Решить уравнение 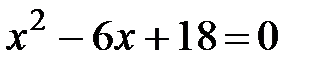 .
.
Решение. Дискриминант данного уравнения: 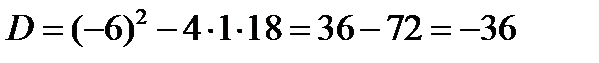 меньше нуля, но теперь мы можем воспользоваться мнимой единицей:
меньше нуля, но теперь мы можем воспользоваться мнимой единицей:
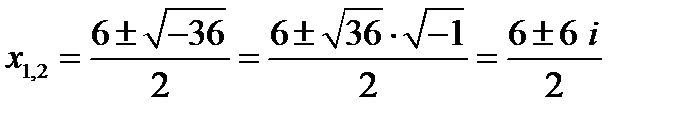 , т.е.
, т.е. 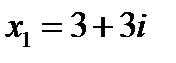 ;
; 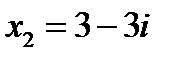 .
.
Справедливы следующие правила арифметических действий над комплексными числами 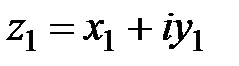 и
и 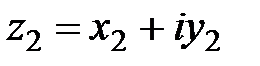 :
:
1) 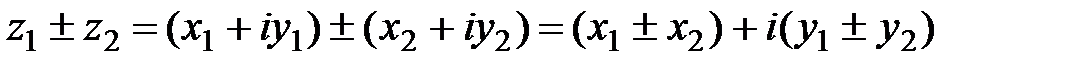 (осуществляется сложение или вычитание алгебраических двучленов и приведение подобных);
(осуществляется сложение или вычитание алгебраических двучленов и приведение подобных);
2) 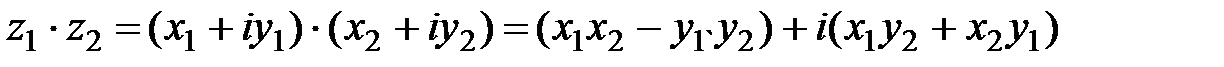 (осуществляется перемножение алгебраических двучленов и приведение подобных с учетом того, что
(осуществляется перемножение алгебраических двучленов и приведение подобных с учетом того, что 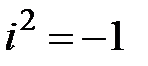 );
);
3) 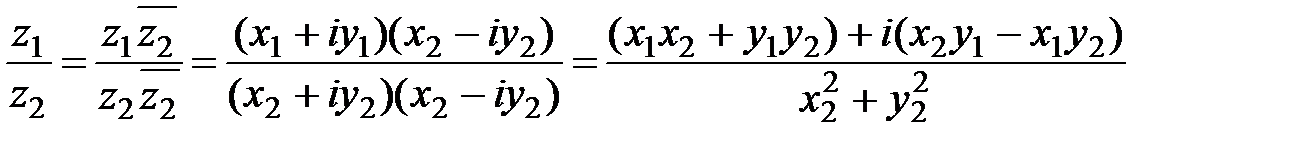 (эта операция возможна только в случае, когда
(эта операция возможна только в случае, когда 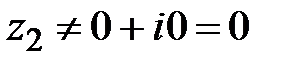 ).
).
Пример 2. Вычислить 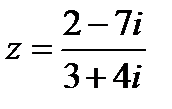 и указать вещественную и мнимую части полученного комплексного числа.
и указать вещественную и мнимую части полученного комплексного числа.
Решение. Действуя в соответствии с правилами получаем:
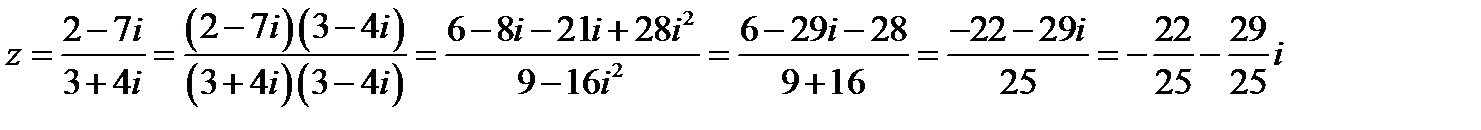 ;
;
поэтому 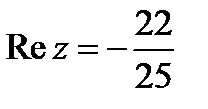 ,
, 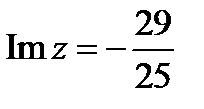 .
.
Тригонометрическая форма комплексного числа. Каждому комплексному числу вида (1.1) можно поставить в соответствие точку M(x;y) на декартовой плоскости (при этом на оси OX располагаются вещественные числа 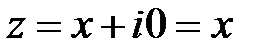 , а на оси OY – чисто мнимые числа
, а на оси OY – чисто мнимые числа 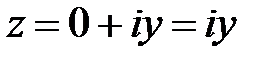 ).
).
Модулем комплексного числа назовем длину отрезка 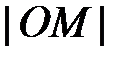 (или расстояние от начала координат до точки M), т.е.
(или расстояние от начала координат до точки M), т.е. 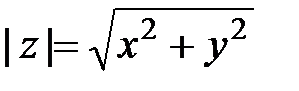 . Аргументом комплексного числа (
. Аргументом комплексного числа (  ) назовем угол, который вектор
) назовем угол, который вектор 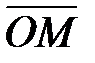 образует с положительным направлением оси OX. Главное значение аргумента, которое, как правило, используется при осуществлении действий с комплексными числами, удовлетворяет условию
образует с положительным направлением оси OX. Главное значение аргумента, которое, как правило, используется при осуществлении действий с комплексными числами, удовлетворяет условию 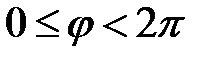 . При этом выражение вида
. При этом выражение вида
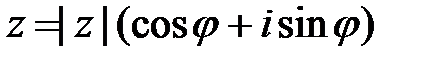 (1.2)
(1.2)
называется тригонометрической формой записи комплексного числа.
Преобразуем (1.1)
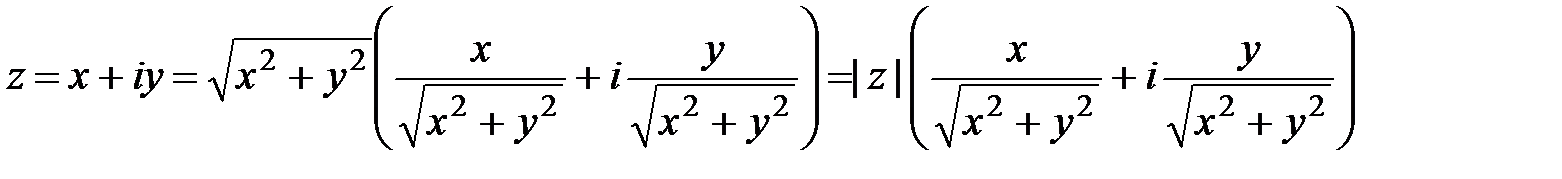
и, сравнивая с (1.2), получаем, что аргумент z можно найти, решив систему
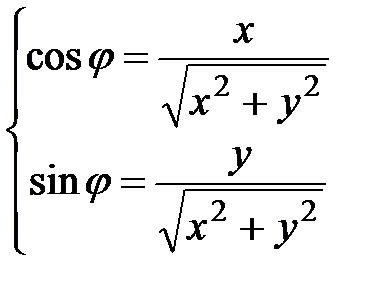 или
или 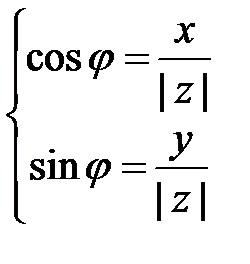 (1.3.)
(1.3.)
Пример 3. Записать комплексное число в тригонометрической форме 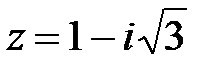 , указать модуль и аргумент комплексного числа.
, указать модуль и аргумент комплексного числа.
Решение. По определению 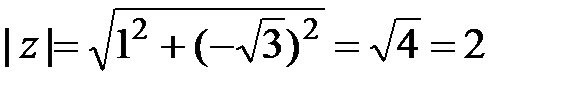 . Для определения аргумента воспользуемся формулой:
. Для определения аргумента воспользуемся формулой: 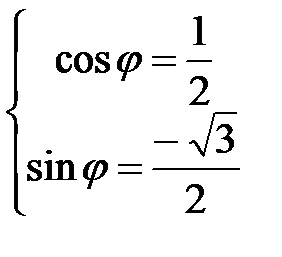 . Получаем, что
. Получаем, что 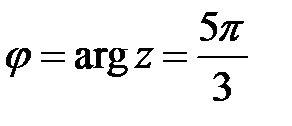 . Тригонометрическая форма заданного комплексного числа имеет вид:
. Тригонометрическая форма заданного комплексного числа имеет вид: 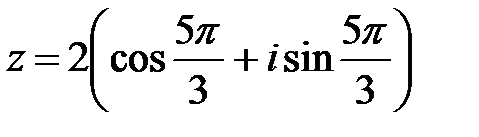 .
.
Возведение в степень и извлечение корней . Если комплексное число задано тригонометрической формой 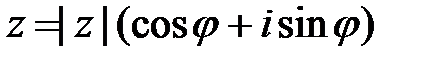 , то справедлива формула Муавра
, то справедлива формула Муавра
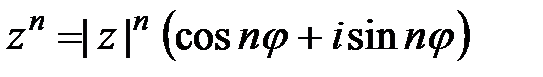 . (1.4)
. (1.4)
Для извлечения корня n-й степени (n – целое число, большее 1) из комплексного числа, заданного в тригонометрической форме, применяется формула, дающая n значений этого корня:
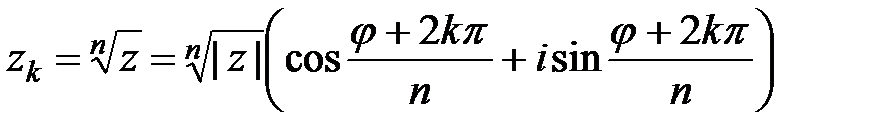 , k=0,1,…,n-1. (1.5)
, k=0,1,…,n-1. (1.5)
Пример 4. Вычислить: a) 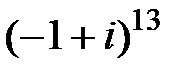 ; b)
; b) 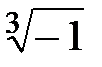 .
.
Решение. В задании a), чтобы воспользоваться формулой Муавра, необходимо представить комплексное число в тригонометрической форме. Имеем: 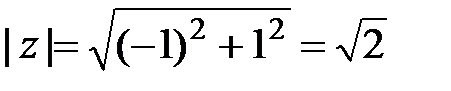 ;
; 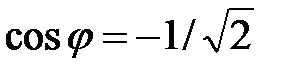 и
и 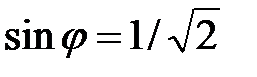 , т.е.
, т.е. 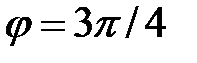 (так как соответствующая точка лежит во второй четверти). Следовательно,
(так как соответствующая точка лежит во второй четверти). Следовательно, 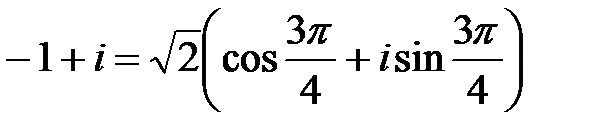 и
и 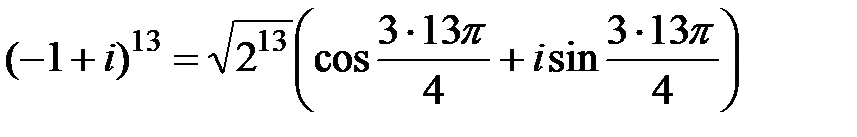 (в силу (1.4)). Учитывая что
(в силу (1.4)). Учитывая что 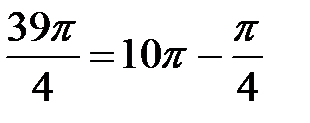 и используя свойства тригонометрических функций, получаем:
и используя свойства тригонометрических функций, получаем:
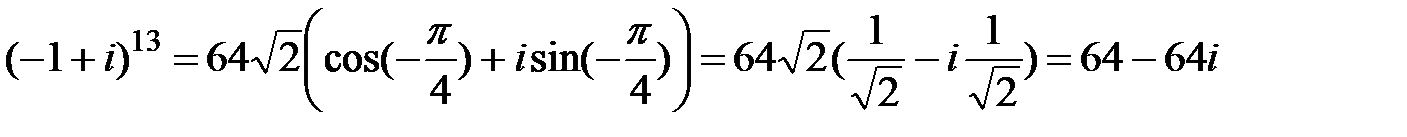 .
.
В задании b) тригонометрическая форма заданного числа имеет вид 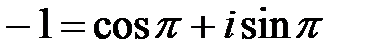 (|z|=1), поэтому в силу (1.5)
(|z|=1), поэтому в силу (1.5)
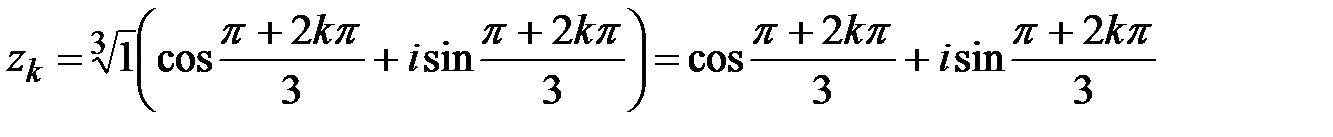 , k=0,1,2.
, k=0,1,2.
Выписываем три искомых корня:
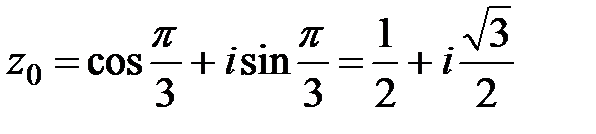 ;
;
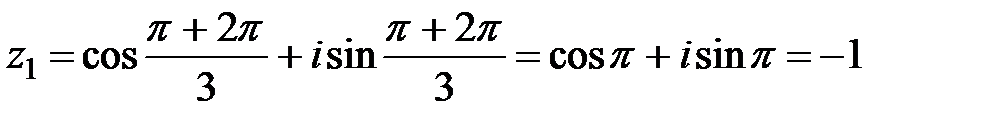 ;
;
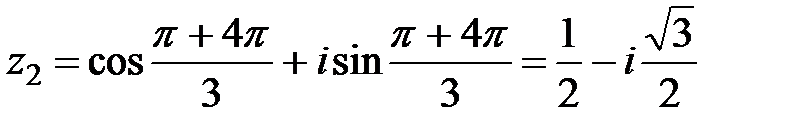 .
.
Решение прикладных задач
Задача 1
Определить ток 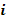 в неразветвленной части, если токи в ветвях:
в неразветвленной части, если токи в ветвях:
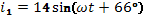
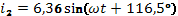
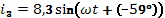
Дано:
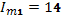 ,
, 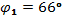
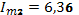 ,
, 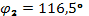
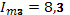 ,
, 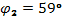
Решение:
Найдем:
1. Комплексные токи в цепях: 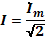
 (А)
(А)
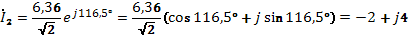 (А)
(А)
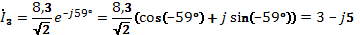 (А)
(А)
2. Комплекс тока в неразветвленной части цепи:
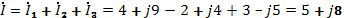
3.Модуль тока:
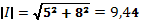 (А)
(А)
4.Аргумент через 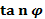 :
:
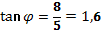 , по таблице Брадиса
, по таблице Брадиса 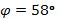
Ответ: 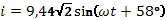
Задача 2
Известно, что
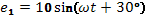
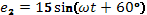
Найти результирующую Э.Д.С.
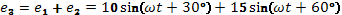
Дано:
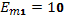 ,
, 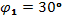
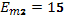 ,
, 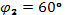
Решение: 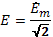
Найдем:
1. Комплексное Э.Д.С. в цепях:
Найдем:
1. Комплексное Э.Д.С. в цепях:
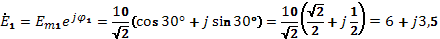
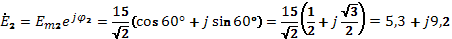
2. Комплекс Э.Д.С. в неразветвленной части цепи:
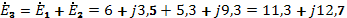
3.Модуль Э.Д.С.:
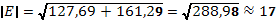
4.Аргумент через 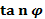 :
:
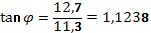 , по таблице Брадиса
, по таблице Брадиса 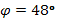
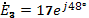
Ответ: 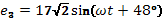
Практическое занятие. Нахождение вероятности.
Цель. Формировать умения и навыки нахождения вероятности, используя классическую формулу.
Решение задач
Пример 1. Найти вероятность, что при бросании монеты выпадет герб.
Решение. При бросании монеты имеются два равновозможных исхода: “выпадение герба” и “выпадение решки” 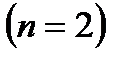 . Для события
. Для события 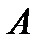 – “выпадение герба” благоприятен только один из них
– “выпадение герба” благоприятен только один из них 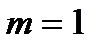 . Значит, вероятность
. Значит, вероятность 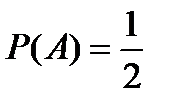 .
.
Вероятность любого события заключена между нулем и единицей 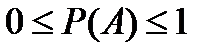
Можно выделить следующие виды случайных событий:
Событие называется достоверным, если оно обязательно происходит при каждом осуществлении определенной совокупности условий. Вероятность достоверного события 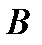 равна единице:
равна единице: 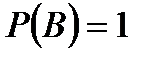 .
.
Событие называется невозможным, если оно заведомо не произойдет ни при одном осуществлении данной совокупности условий. Вероятность невозможного события 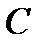 равна нулю:
равна нулю: 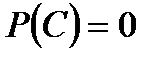 .
.
Событие называется случайным, если оно может произойти, а может и не произойти при осуществлении данной совокупности условий.
События называются несовместными, если их одновременное появление при осуществлении комплекса условий невозможно, т.е. появление события 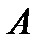 в данном испытании исключает появление события
в данном испытании исключает появление события 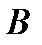 в этом же испытании.
в этом же испытании.
События называются единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием.
События называются равновозможными, если есть основания считать, что ни одно из этих событий не является более возможным, чем другие.
Если событие 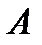 - какое-либо событие, то событие, состоящее в том, что событие
- какое-либо событие, то событие, состоящее в том, что событие 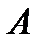 не наступило, называется противоположным событию
не наступило, называется противоположным событию 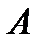 и обозначается как
и обозначается как 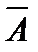 .
.
События, происходящие при реализации определенного комплекса условий или в результате случайного эксперимента, называются элементарными исходами.
Считается, что при проведении случайного эксперимента реализуется только один из возможных элементарных исходов.
Геометрической вероятностью события A называется отношение площади области g к площади области G, т. е.
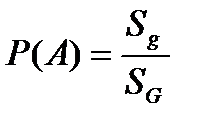
Область g называется благоприятствующей (благоприятной) событию A.
Область, на которую распространяется понятие геометрической вероятности, может быть одномерной (прямая, отрезок) и трехмерной (некоторое тело в пространстве). Обозначая меру (длину, площадь, объем) области через mes, можно записать
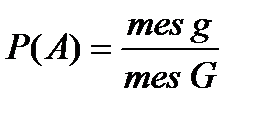
Примеры:
1. В некоторой точке C линии AB длины L произошел разрыв. Какова вероятность того, что точка C удалена от точки A на расстояние не меньше 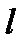 ?
?
Решение.
Расположим отрезок AB на числовой оси Ox так, как изображено на рис. 2.
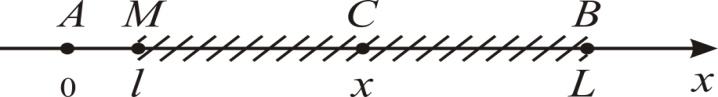
Рис. 2
Пусть x – координата случайной точки C отрезка AB, 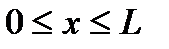 . Ясно, что исходов опыта (разрыв линии AB в точке C) бесчисленное множество и все они равновозможны. На отрезке AB возьмем точку M, расстояние которой от точки A, равно
. Ясно, что исходов опыта (разрыв линии AB в точке C) бесчисленное множество и все они равновозможны. На отрезке AB возьмем точку M, расстояние которой от точки A, равно 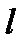 .
.
Очевидно, что событие A={точка C удалена от точки A на расстояние не меньше 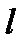 } произойдет, если точка C попадет на отрезок MB=[
} произойдет, если точка C попадет на отрезок MB=[ 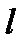 ,L].
,L].
Таким образом, областью, благоприятствующей наступлению события A (на рис. 2 она заштрихована), является отрезок MB, а множеству исходов опыта соответствует отрезок AB=[0,L].
Тогда по формуле (3)
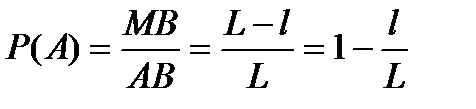 .
.
2. Сколькими способами можно расставить на полке 5 различных книг?
Решение. Искомое число способов равно числу перестановок из 5 элементов (книг), т. е. 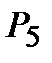 = 5! = 1·2·3·4·5 = 120.
= 5! = 1·2·3·4·5 = 120.
3. Сколько «слов» по две буквы можно составить из букв a , b , c , d , e , таким образом, чтобы буквы в «словах» не повторялись?
Решение. Т.к. каждое «слово» должно содержать две буквы, то искомое число способов равно числу размещений из 5 элементов (букв) по две, т. е. 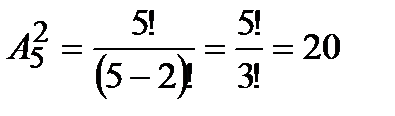 .
.
4. Сколькими способами можно выбрать 1 красную гвоздику и 2 розовых из вазы, в которой стоят 10 красных и 4 розовых гвоздики?
Решение. Так как порядок выбора цветов не имеет значения, то красную гвоздику можно выбрать 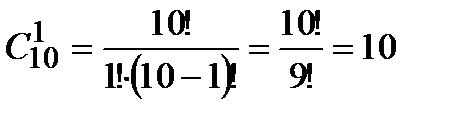 способами. Выбрать две розовые гвоздики из имеющихся четырех можно
способами. Выбрать две розовые гвоздики из имеющихся четырех можно 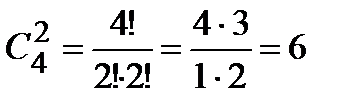 способами. Поэтому букет из одной красной и двух розовых гвоздик можно составить, по правилу умножения,
способами. Поэтому букет из одной красной и двух розовых гвоздик можно составить, по правилу умножения, 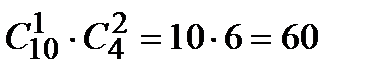 способами.
способами.
5. Набирая номер телефона, абонент забыл последние 3 цифры, и помня лишь, что эти цифры различны, набрал их наугад. Найти вероятность того, что номер телефона набран правильно.
Решение. Благоприятствующий исход здесь один – правильный набор последних цифр 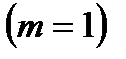 . Всех возможных исходов здесь будет столько, сколько можно составить комбинаций из 3 цифр, порядок которых имеет значение, значит
. Всех возможных исходов здесь будет столько, сколько можно составить комбинаций из 3 цифр, порядок которых имеет значение, значит 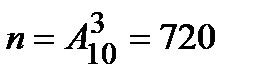 . Значит вероятность того, что номер набран правильно (событие
. Значит вероятность того, что номер набран правильно (событие 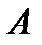 ):
): 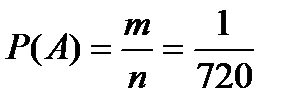 .
.
6. Среди 100 колес 5 нестандартных. Для контроля выбирается 7 колес. Найти вероятность того, что среди них ровно 3 будет нестандартных.
Решение. Число всевозможных исходов равно количеству комбинаций из 100 колес по 7 штук, т.к. порядок значения не имеет, то 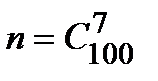 . Благоприятствующий исход состоит в выборе ровно 3 нестандартных колес из 5 и совместном выборе (7-3) стандартных колес из (100-5), порядок значения не имеет. По правилу произведения
. Благоприятствующий исход состоит в выборе ровно 3 нестандартных колес из 5 и совместном выборе (7-3) стандартных колес из (100-5), порядок значения не имеет. По правилу произведения 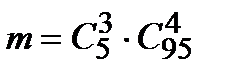 . Следовательно, вероятность того, что среди взятых для контроля колес будет ровно 3 нестандартных (событие
. Следовательно, вероятность того, что среди взятых для контроля колес будет ровно 3 нестандартных (событие 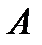 ):
): 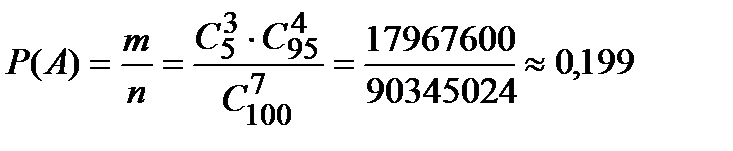 .
.
Практическое занятие. Нахождение математического ожидания дискретной случайной величины.
Цель. Формировать умения и навыки нахождения математического ожидания дискретной величины.
Решение задач
Наиболее исчерпывающей характеристикой случайной величины является ее закон распределения вероятностей. Однако не всегда обязательно знать весь закон распределения. Иногда можно обойтись одним или несколькими числами, отражающими наиболее важные особенности закона распределения, например, числом, имеющим смысл «среднего значения» случайной величины, или же числом, показывающим средний размер отклонения случайной величины от своего среднего значения. Такого рода числа называются числовыми характеристиками случайной величины. Оперируя числовыми характеристиками, можно решать многие задачи, не пользуясь законом распределения.
Одна из самых важных числовых характеристик случайной величины есть математическое ожидание.
Если известна дискретная случайная величина 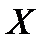 , закон распределения которой имеет вид
, закон распределения которой имеет вид
Значения 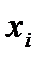
| 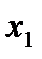
| 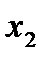
| … | 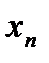
|
Вероятности 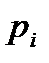
| 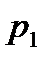
| 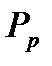
| … | 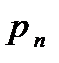
|
то математическим ожиданием (или средним значением) дискретной величины 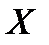 называется число
называется число
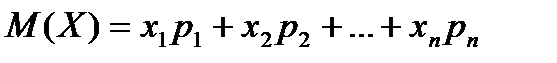 .
.
Таким образом, математическое ожидание дискретной случайной величины 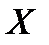 равно сумме произведений возможных значений этой величины на их вероятности.
равно сумме произведений возможных значений этой величины на их вероятности.
Свойства математического ожидания.
1. Постоянный множитель можно выносить за знак математического ожидания:
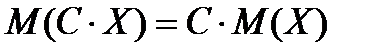
2. Математическое ожидание постоянной величины С равно самой этой величине:
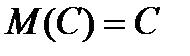
3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
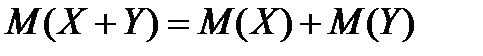 .
.
4. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий этих величин:
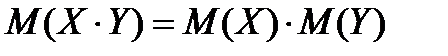 .
.
Свойства дисперсии.
1. Дисперсия постоянной величины С равна 0:
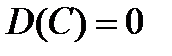 .
.
2. Если 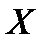 - случайная величина, аС – постоянная, то
- случайная величина, аС – постоянная, то
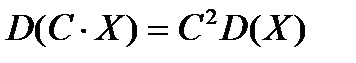
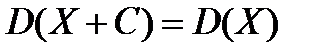 .
.
3. Если 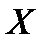 и
и 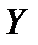 - независимые случайные величины, то
- независимые случайные величины, то
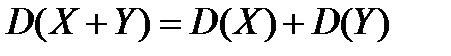 .
.
4. Для вычисления дисперсий более удобной является формула
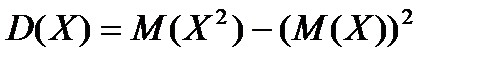 .
.
Пример 3. Дискретная случайная величина распределена по закону:
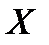
| -1 | 0 | 1 | 2 |
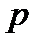
| 0,2 | 0,1 | 0,3 | 0,4 |
Найти 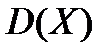 .
.
Решение. Сначала находим 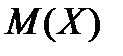 .
.
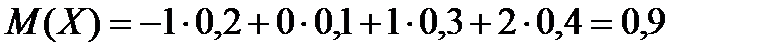 ,
,
а затем 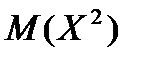 .
.
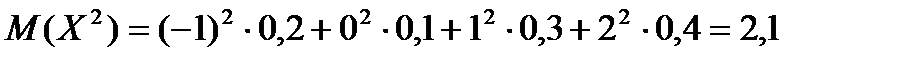 .
.
По формуле 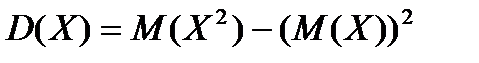 имеем
имеем
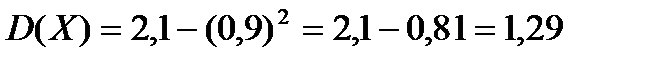 .
.
Средним квадратичным отклонением случайной величины называется корень квадратный из ее дисперсии:
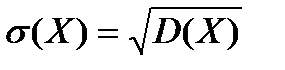 .
.
Пример 1. 1) Найти математическое ожидание, дисперсию, среднее квадратическое отклонение и 2) функцию распределения дискретной случайной величины Х, заданной законом распределения:
| х | -5 | 2 | 3 | 4 |
| р | 0,4 | 0,3 | 0,1 | 0,2 |
Решение
1) 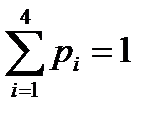
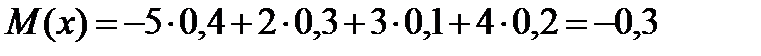
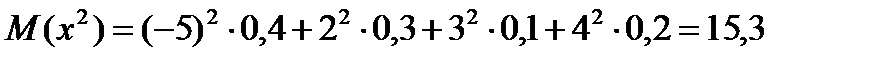
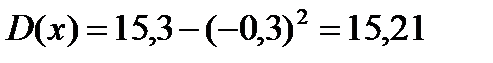
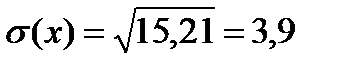
2) Будем задавать различные значения х и находить для них 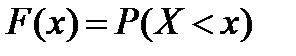
1. Если 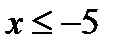 , то F(
, то F(  )=0, F(1)=0;
)=0, F(1)=0;
2. при –5< 
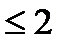 , F(
, F(  )=P(
)=P(  =-5)=0,4; F(2)=P(
=-5)=0,4; F(2)=P(  <2)=0,4;
<2)=0,4;
3. при 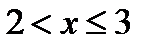 , F(
, F(  )=P(X<
)=P(X<  )=P(
)=P(  =-5)+P(
=-5)+P(  =2)=0,7; F(3)=0,7;
=2)=0,7; F(3)=0,7;
4. при 
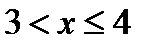 , F(X<
, F(X<  )=P(
)=P(  =-5)+P(
=-5)+P(  =2)+P(
=2)+P(  =3)=0,8; F(4)=0,8;
=3)=0,8; F(4)=0,8;
5. при  >4, F(
>4, F(  )=P(
)=P(  =-5)+P(
=-5)+P(  =2)+P(
=2)+P(  =3)+P(
=3)+P(  =4)=1.
=4)=1.
F(  )=
)= 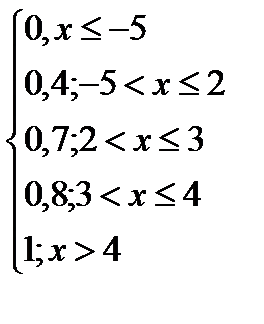

Ответ: -0,3; 15,21; 3,9; F(  ).
).
Практическое занятие. Вычисление пределов
Цель: Формировать умения и навыки вычисления пределов функции
Решение задач
Пример . Найти
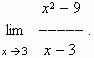
Решение . Подставляя x = 3 в выражение 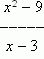 получим не имеющее смысла выражение
получим не имеющее смысла выражение 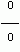 . Поэтому решим по-другому:
. Поэтому решим по-другому:
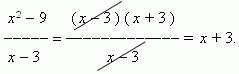
Сокращение дроби в данном случае корректно, так как x  3 , он лишь приближается к 3. Теперь мы имеем:
3 , он лишь приближается к 3. Теперь мы имеем: 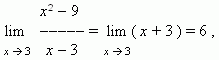
поскольку, если x стремится к 3, то x + 3 стремится к 6 .
Замечательные пределы
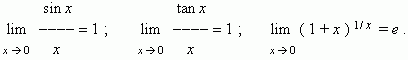
Бесконечно малая и бесконечно большая величины. Если предел некоторой переменной равен 0, то эта переменная называется бесконечно малой.
Пример . Функция y = 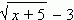 является бесконечно малой при x,
является бесконечно малой при x,
стремящемся к 4, так как 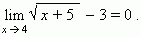
Если абсолютное значение некоторой переменной неограниченно возрастает, то эта переменная называется бесконечно большой.

Бесконечно большая величина не имеет конечного предела, но она имеет так называемый бесконечный предел, что записывается как:
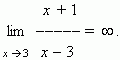
Символ 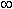 (бесконечность ) не означает некоторого числа, он означает только, что дробь неограниченно возрастает при x, стремящемся к 3. Следует отметить, что дробь может быть как положительной ( при x > 3 ), так и отрицательной ( при x < 3 ). Если бесконечно большая величина может быть только положительной при любых значениях x, это отражается в записи. Например, при x
(бесконечность ) не означает некоторого числа, он означает только, что дробь неограниченно возрастает при x, стремящемся к 3. Следует отметить, что дробь может быть как положительной ( при x > 3 ), так и отрицательной ( при x < 3 ). Если бесконечно большая величина может быть только положительной при любых значениях x, это отражается в записи. Например, при x 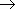 0 функция y = x2 бесконечно большая, но она положительна как при x > 0, так и при x < 0 ; это выражается так:
0 функция y = x2 бесконечно большая, но она положительна как при x > 0, так и при x < 0 ; это выражается так:
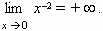
Наоборот, функция y = x 2 всегда отрицательна, поэтому
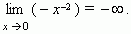
В соответствии с этим, результат в нашем примере можно записать так:
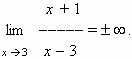

Вычисление пределов (для самостоятельного выполнения заданий)
1.Найдите пределы последовательностей:
1) 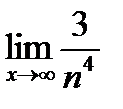 ; 3)
; 3) 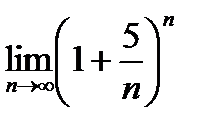 ;
;
2) 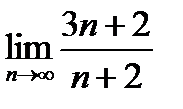 ; 4)
; 4) 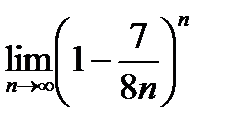 .
.
2.Найдите пределы функций:
1) 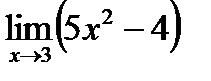 ;
;
2) 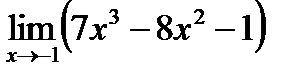 ;
;
3) 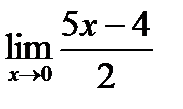 ;
;
4) 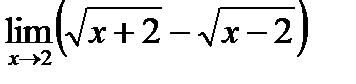 ;
;
5) 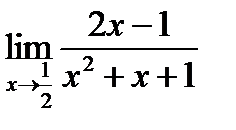 .
.
3. Раскрытие неопределенностей вида 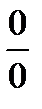 . Найдите пределы:
. Найдите пределы:
1) 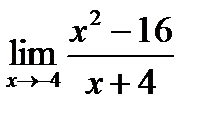 ; 3)
; 3) 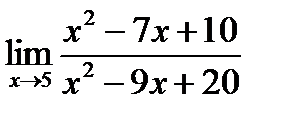 ;
;
2) 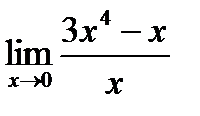 ; 4)
; 4) 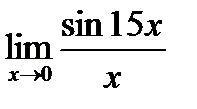 .
.
4. Раскрытие неопределенностей вида 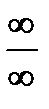 . Найдите пределы:
. Найдите пределы:
1) 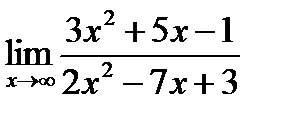 ; 2)
; 2) 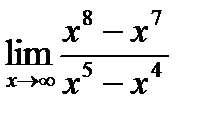 .
.
Практическое занятие. Исследование функций на непрерывность.
Цель: Формировать умения и навыки исследования функций на непрерывность
Решение задач
Пример 1 Пусть 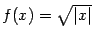 и
и 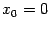 . Тогда
. Тогда 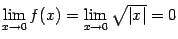 и
и 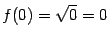 . Эти значения совпадают, значит, функция
. Эти значения совпадают, значит, функция 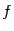 непрерывна в точке
непрерывна в точке 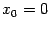 .
.
(Функция 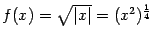 ‒ элементарная функция;
‒ элементарная функция; 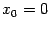 ‒ точка её области определения
‒ точка её области определения 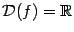 . Все элементарные функции непрерывны во всех внутренних точках своих областей определения, в том числе и эта. Так что в этом примере можно было бы заменить
. Все элементарные функции непрерывны во всех внутренних точках своих областей определения, в том числе и эта. Так что в этом примере можно было бы заменить 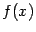 любой элементарной функцией, а
любой элементарной функцией, а 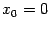 -- любой внутренней точкой области
-- любой внутренней точкой области 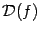 , и вывод остался бы тем же.)
, и вывод остался бы тем же.)
Пример 2 Рассмотрим функцию 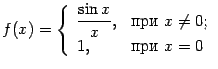 и точку
и точку 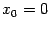 . При
. При 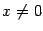 функция задаётся формулой
функция задаётся формулой 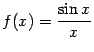 , при этом имеем
, при этом имеем 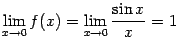 (первый замечательный предел). Это значение совпадает с тем, которое задано при
(первый замечательный предел). Это значение совпадает с тем, которое задано при 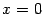 :
: 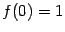 . Итак,
. Итак, 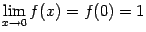 , что означает непрервыность функции
, что означает непрервыность функции 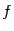 при
при 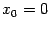 .
.
Тем, кто внимательно изучил данное в главе 2 общее понятие базы предела, можно предложить продумать и доказать следующее утверждение:
Определение точек разрыва
Дадим теперь определение точек разрыва функции.
Определение Точка  называется точкой разрыва функции
называется точкой разрыва функции 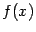 , если она определена в некоторой проколотой окрестности точки
, если она определена в некоторой проколотой окрестности точки  (то есть, определена на некотором интервале, для которого
(то есть, определена на некотором интервале, для которого  служит внутренней точкой, но в самой точке
служит внутренней точкой, но в самой точке  , возможно, не определена) и выполняется, хотя бы одно из следующих условий:
, возможно, не определена) и выполняется, хотя бы одно из следующих условий:
1) не существует предела слева 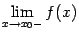 ;
;
2) не существует предела справа 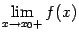 ;
;
3) пределы слева 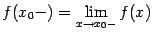 и справа
и справа 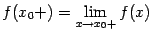 существуют, но не равны друг другу:
существуют, но не равны друг другу: 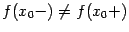 ;
;
4) пределы слева 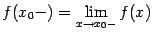 и справа
и справа 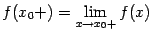 существуют и равны друг другу:
существуют и равны друг другу: 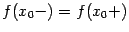 , но не совпадают со значением функции в точке
, но не совпадают со значением функции в точке  :
: 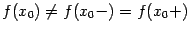 , или функция
, или функция 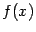 не определена в точке
не определена в точке  .
.
Если имеет место либо случай 3, либо случай 4, то точка разрыва  называется точкой разрыва первого рода, а поведение функции в окрестности точки
называется точкой разрыва первого рода, а поведение функции в окрестности точки  называется разрывом первого рода в точке
называется разрывом первого рода в точке  ; в случае 4 точка разрыва первого рода называется устранимой точкой разрыва, а разрыв функции в этой точке -- устранимым разрывом.
; в случае 4 точка разрыва первого рода называется устранимой точкой разрыва, а разрыв функции в этой точке -- устранимым разрывом.
Если же имеет место либо случай 1, либо случай 2 (либо и тот и другой сразу), то точка разрыва  называется точкой разрыва второго рода, а поведение функции в окрестности этой точки ‒ разрывом второго рода в точке
называется точкой разрыва второго рода, а поведение функции в окрестности этой точки ‒ разрывом второго рода в точке  .
.
Итак, если функция 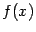 имеет разрыв первого рода в точке
имеет разрыв первого рода в точке  , то существуют, как часто говорят, значения функции "на берегах разрыва":
, то существуют, как часто говорят, значения функции "на берегах разрыва": 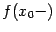 и
и 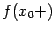 , но точка
, но точка  не является точкой непрерывности.
не является точкой непрерывности.
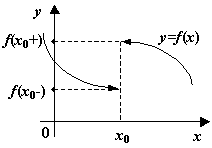
.  -- точка разрыва первого рода
-- точка разрыва первого рода
Если значения на берегах разрыва разные, то значение функции в точке  может быть любым (или вообще отсутствовать), всё равно
может быть любым (или вообще отсутствовать), всё равно  будет давать разрыв первого рода. Если же значения на берегах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке
будет давать разрыв первого рода. Если же значения на берегах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке  , либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию
, либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию 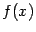 в точке
в точке  , положив
, положив 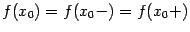 , то полученная изменённая функция будет уже непрерывна в точке
, то полученная изменённая функция будет уже непрерывна в точке  и разрыв в точке
и разрыв в точке  исчезнет; отсюда и название такого разрыва ‒ устранимый.
исчезнет; отсюда и название такого разрыва ‒ устранимый.
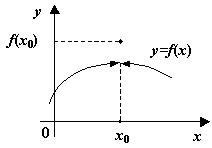
.  -- точка устранимого разрыва
-- точка устранимого разрыва
Наконец, к разрывам второго рода, как видно из определения, относятся все разрывы, которые не принадлежат к разрывам первого рода; некоторые из возможных способов поведения функции в окрестности точки  , где происходит разрыв второго рода, представлены на следующем рисунке.
, где происходит разрыв второго рода, представлены на следующем рисунке.
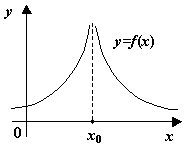
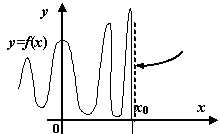
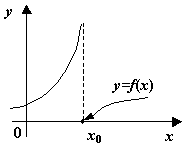
.  -- точка разрыва второго рода. Некоторые возможные варианты
-- точка разрыва второго рода. Некоторые возможные варианты
Пример 3 Рассмотрим функцию 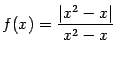 , для которой
, для которой
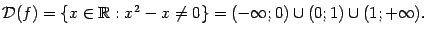
Функция имеет разрывы при 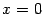 и при
и при 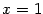 . Нетрудно видеть, что при
. Нетрудно видеть, что при 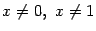
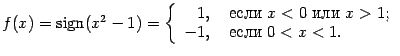 В точках
В точках 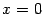 и
и 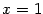 функция имеет неустранимые разрывы первого рода. В точке
функция имеет неустранимые разрывы первого рода. В точке 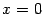 имеем:
имеем:
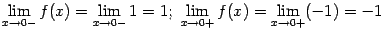
(значения на краях разыва существуют, но не совпадают); в точке 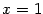 ‒
‒
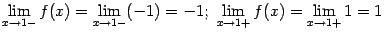
(снова пределы слева и справа существуют, но не совпадают).
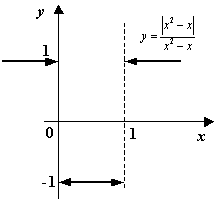
График функции 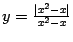
Пример 4 Функция 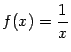 имеет при
имеет при 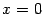 разрыв второго рода, так как
разрыв второго рода, так как 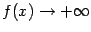 при
при 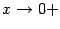 и
и 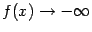 при
при 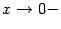 .
.
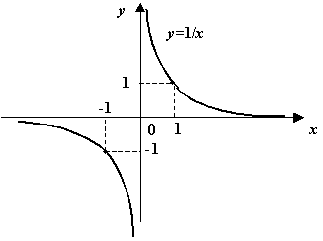
Рис.3.6.График функции 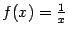
Пример 5 Функция 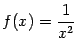 имеет при
имеет при 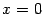 разрыв второго рода, так как
разрыв второго рода, так как 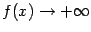 при
при 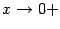 и при
и при 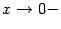 .
.
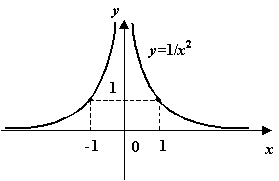
Рис. График функции 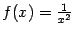
Первый замечательный предел равен 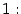
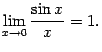
Вторым замечательным пределом называется предел
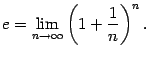
Число 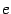 , заданное этим пределом, играет очень большую роль, как в математическом анализе, так и в других разделах математики. Число
, заданное этим пределом, играет очень большую роль, как в математическом анализе, так и в других разделах математики. Число 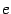 часто называют основанием натуральных логарифмов.
часто называют основанием натуральных логарифмов.
Второй замечательный предел существует. Его значение 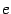 ‒ число, лежащее между 2 и
‒ число, лежащее между 2 и 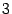 .
.
Более подробное изучение числа 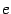 показывает, что
показывает, что 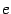 ‒ иррациональное число, несколько первых десятичных знаков которого таковы:
‒ иррациональное число, несколько первых десятичных знаков которого таковы:
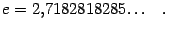
Пример 6. Найдём предел 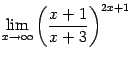 .
.
Здесь основание степени имеет предел
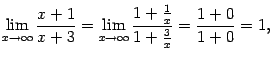
а показатель степени 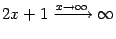 . Поэтому можно применять тот же приём сведения ко второму замечательному пределу, что в предыдущем примере. Для начала найдём, что следует взять за бесконечно малую величину
. Поэтому можно применять тот же приём сведения ко второму замечательному пределу, что в предыдущем примере. Для начала найдём, что следует взять за бесконечно малую величину 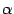 . Поскольку основание степени стремится к 1, то оно равно
. Поскольку основание степени стремится к 1, то оно равно 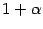 , где
, где 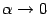
Значит,
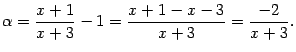
Теперь преобразуем функцию, стоящую под знаком предела:
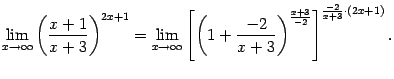
Выражение, стоящее в квадратных скобках, имеет вид 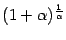 и при
и при 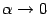 стремится к числу
стремится к числу 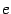 (это второй замечательный предел), а предел показателя степени мы найдём отдельно:
(это второй замечательный предел), а предел показателя степени мы найдём отдельно:
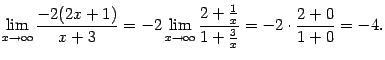
Поэтому
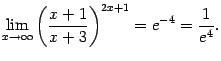
(
Практическое занятие. Нахождение производной функции.
Цель: Приобрести навыки вычисления производной функции.
Справочный материал и примеры
Производной функции 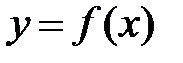 называется конечный предел отношения приращения функции
называется конечный предел отношения приращения функции 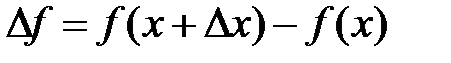 к приращению независимой переменной
к приращению независимой переменной 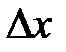 при стремлении последнего к нулю:
при стремлении последнего к нулю:
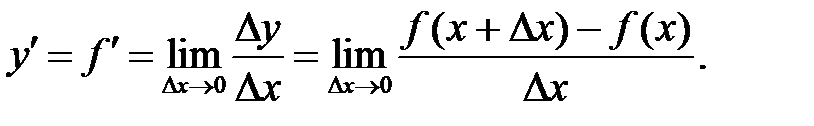 (1)
(1)
Обозначения производной в точке х0:
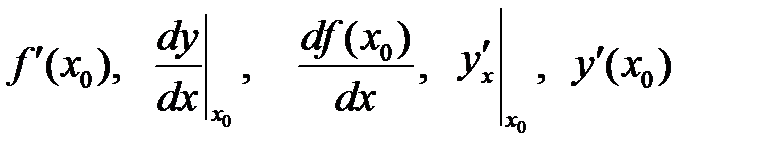 и другие.
и другие.
Если функция в точке х0 (или на промежутке Х) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке Х).
Процесс отыскания производной называется дифференцированием.

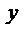
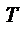
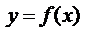
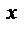
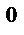
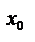
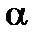
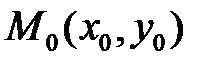
N
Геометрический смысл производной. 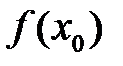
Если кривая задана уравнением 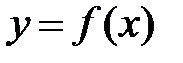 ,
,
то 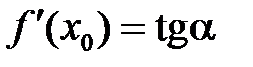 — угловой коэффициент касательной к графику функции в этой точке (
— угловой коэффициент касательной к графику функции в этой точке ( 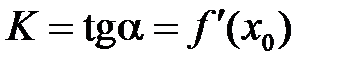 ).
).
Уравнение касательной к кривой 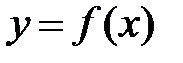
в точке х0 (прямая М0Т) имеет вид:
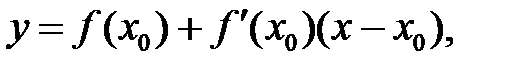 (2)
(2)
а уравнение нормали (М0N):
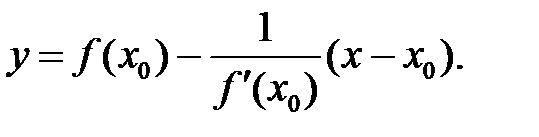 (3)
(3)
Правила дифференцирования
| № пп | U = u(x), V=V(x) — дифференцируемые функции | № п/п | U = u(x), V=V(x) – дифференцируемые функции |
| I | 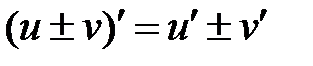
| VI | Производная сложной функции 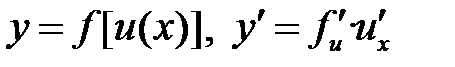
|
| II | 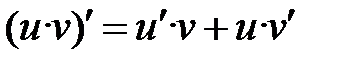
|
VII
Функция задана параметрическими уравнениями 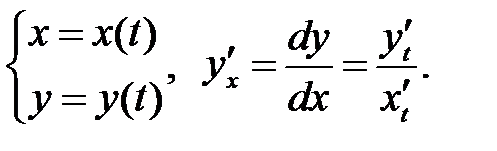
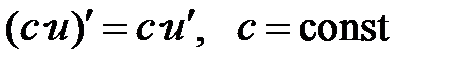
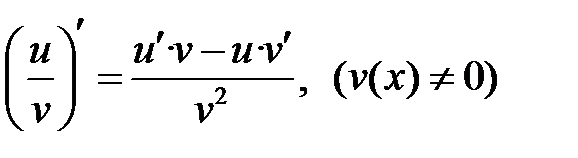
VIII
Если 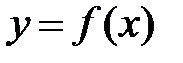 и
и 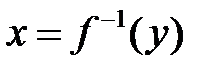 —
—
взаимно обратные функции,
то 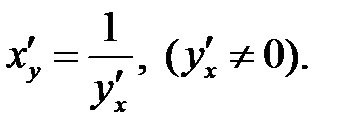
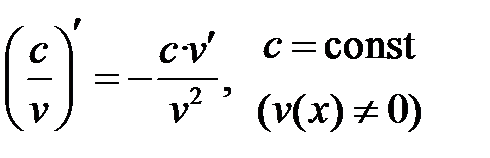
Формулы дифференцирования
| № | Производная элементарной функции |
| 1 | 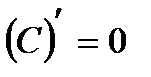
|
| Степенная функция | |
| 2 | 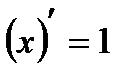
|
| 3 | 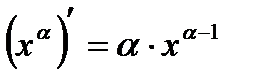
|
| 4 | 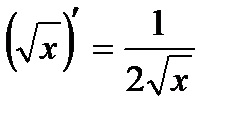
|
| 5 | 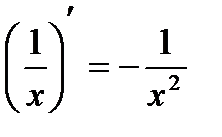
|
| Показательная функция | |
| 6 | 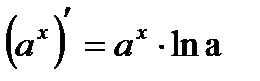
|
| 7 | 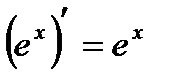
|
| Логарифмическая функция | |
| 8 | 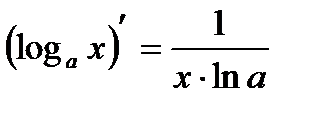
|
| 9 | 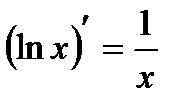
|
| 10 | 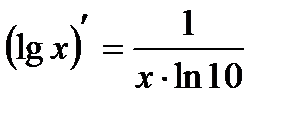
|
| Тригонометрическая функция | |
| 11 | 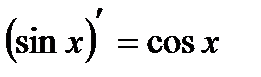
|
| 12 | 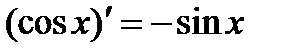
|
| 13 | 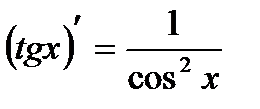
|
| 14 | 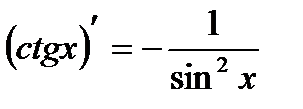
|
| Обратная тригонометрическая функция | |
| 15 | 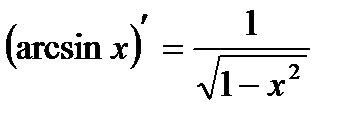
|
| 16 | 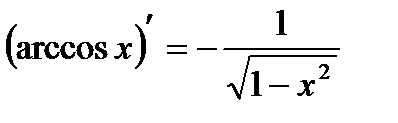
|
| 17 | 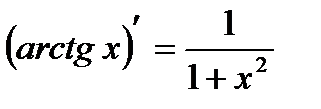
|
| 18 | 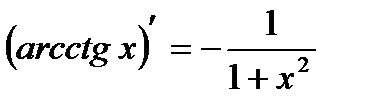
|
Пример 1. Найти производные функций:
а) 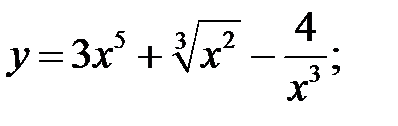 б)
б) 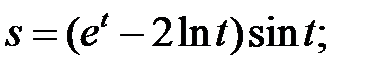 в)
в) 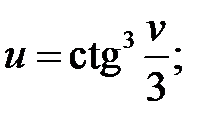 г)
г) 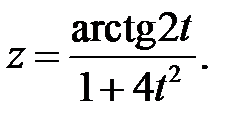
Решение.
а) Используя правила I, III и формулу (3), получим:
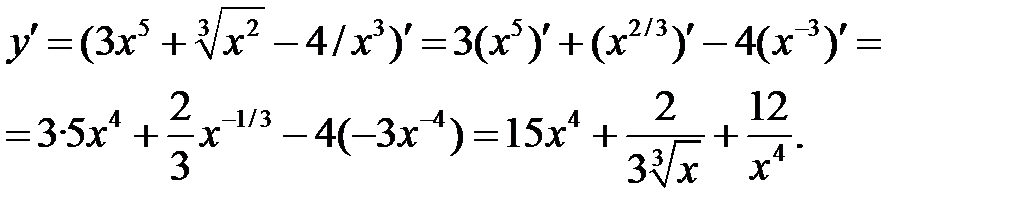
б) Используя правила дифференцирования произведения функций II, разности I, формулы (5), (7), (8) и учитывая, что независимая переменная есть t, т. е. t=1, получим:
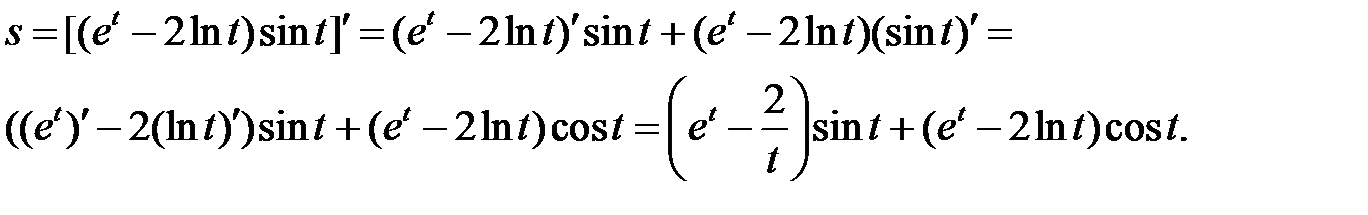
в) Используя правила дифференцирования частного IV, суммы I, III
и формулы (3), (14), учитывая, что t=1, получим:
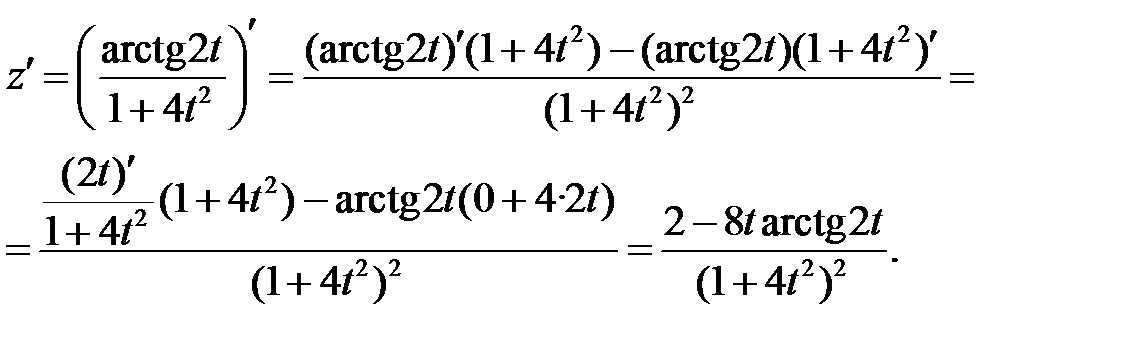
Пример 2. Составить уравнение касательной и нормали к кривой 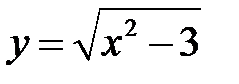 в точке с абсциссой х0=2.
в точке с абсциссой х0=2.
Используем уравнения касательной (2) и нормали (3):
1) 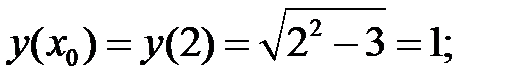
2) 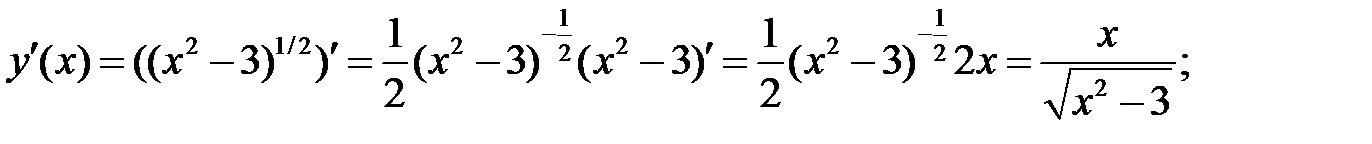
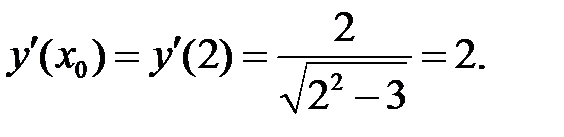
Подставим 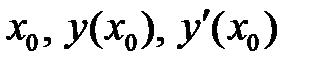 в уравнения и получим:
в уравнения и получим: 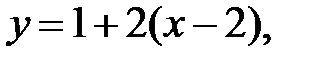
или 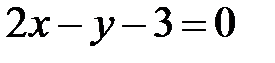 — уравнение касательной.
— уравнение касательной.
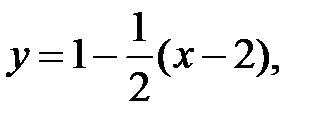 или
или 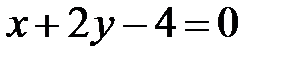 — уравнение нормали.
— уравнение нормали.
Пример 3 . Найти производную 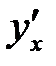 , если функция задана параметрически:
, если функция задана параметрически: 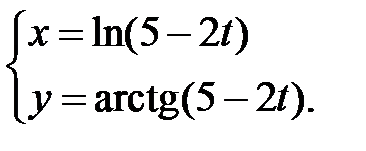
Используем правило VII 
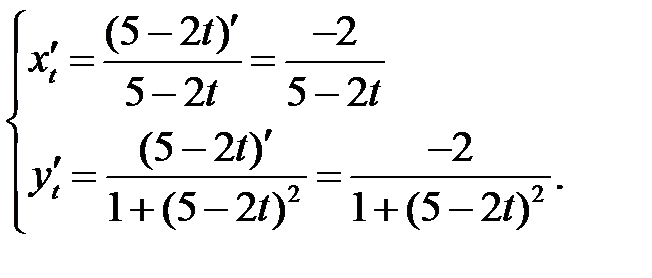
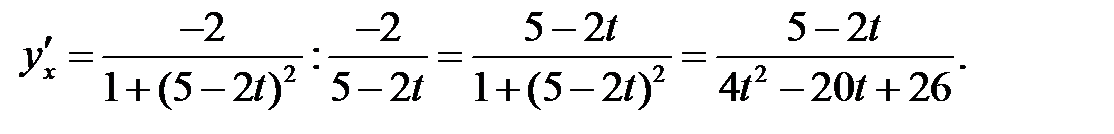
Пример 4. Найти дифференциалы функций:
а) 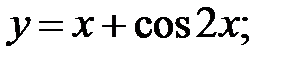 б)
б) 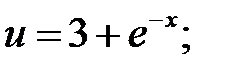 в)
в) 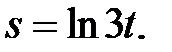
Для дифференциала функции 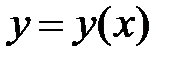 справедлива формула
справедлива формула 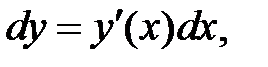 т. е. дифференциал функции равен произведению производной от функции на дифференциал независимой переменной.
т. е. дифференциал функции равен произведению производной от функции на дифференциал независимой переменной.
Решение.
а) 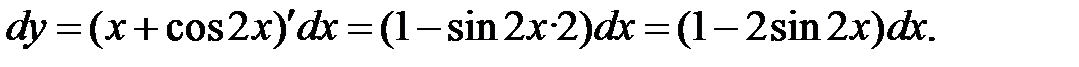
б) 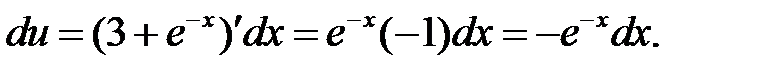
в) 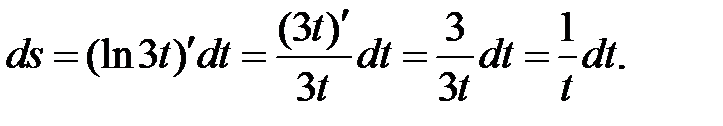
Пример 5. Найти производную функции 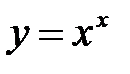 логарифмическим дифференцированием
логарифмическим дифференцированием
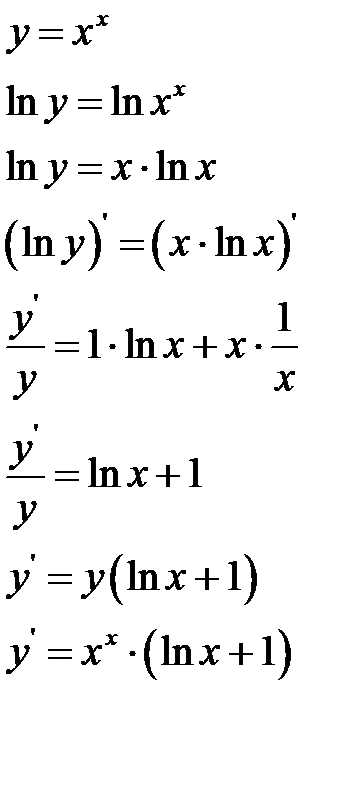
Правило Лопиталя. Предел отношения двух б.м. 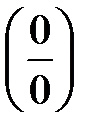 или б.б.
или б.б. 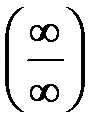 функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:
функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:
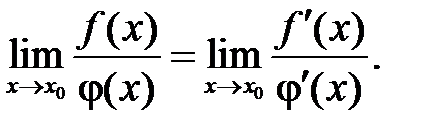 (5)
(5)
Чтобы использовать правило Лопиталя для раскрытия неопределённостей других типов, выражение под знаком предела следует преобразовать элементарными способами так, чтобы получить неопределенность 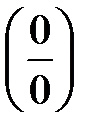 или
или 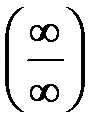 и затем использовать формулу (5).
и затем использовать формулу (5).
Пример 6. Найти пределы, используя правило Лопиталя или элементарные способы раскрытия неопределённостей:
а) 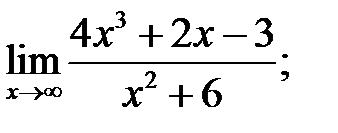 б)
б) 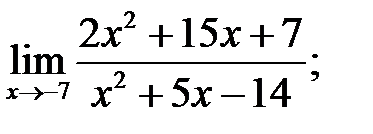
Решение.
а) Подставляя в функцию вместо х предельное значение 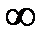 , определим предел числителя и знаменателя.
, определим предел числителя и знаменателя.
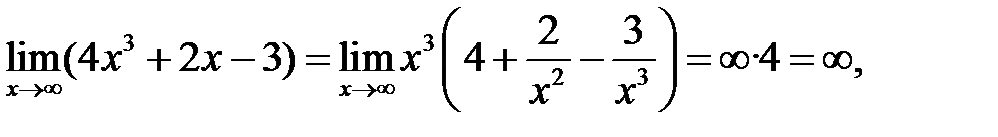 т. к.
т. к. 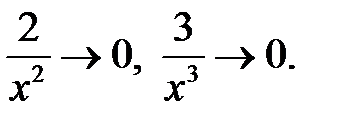
Аналогично: 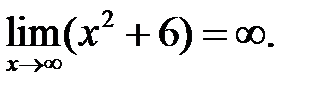
Имеем неопределенность вида 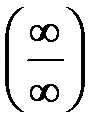 . Используем правило Лопиталя:
. Используем правило Лопиталя:
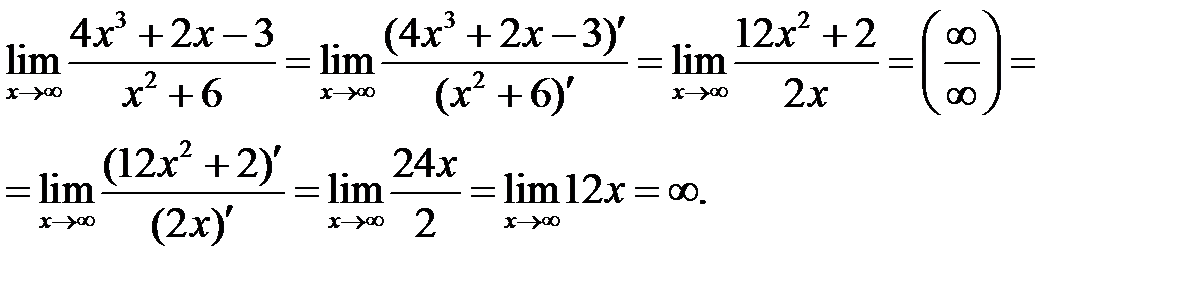
б) 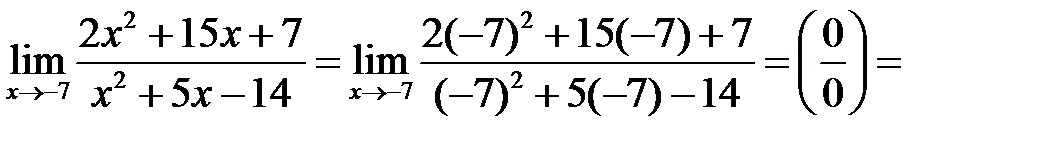
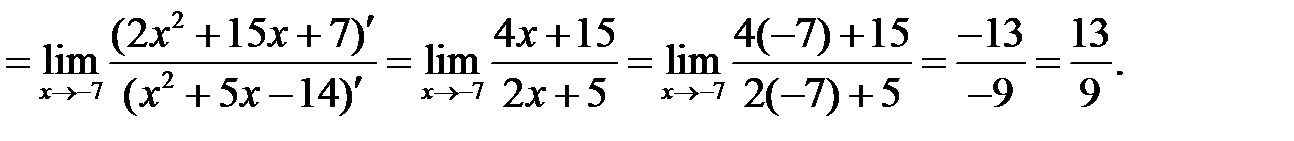
Задания для практической работы
Задание 1. Найти производные 1-го порядка данных функций
1) 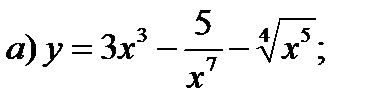
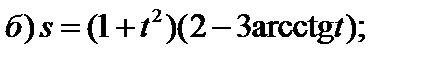
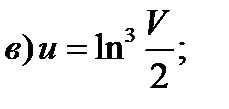
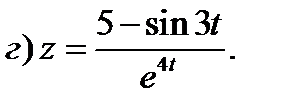
2) 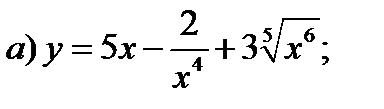
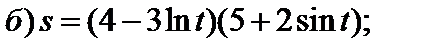
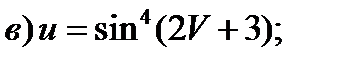
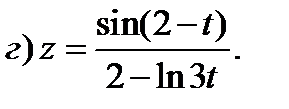
3) 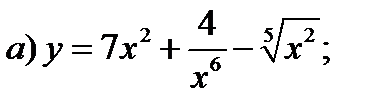
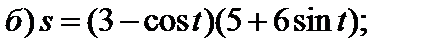
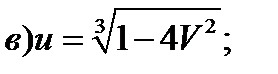
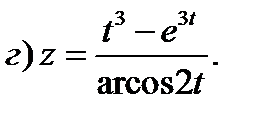
4) 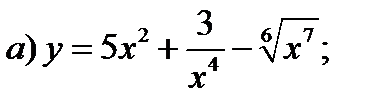
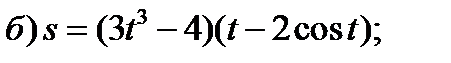
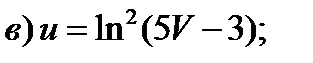
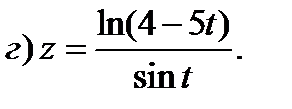
5) 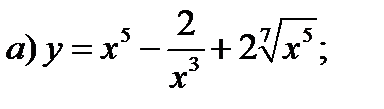
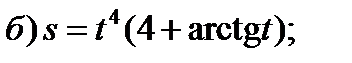
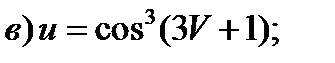
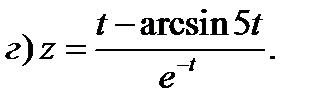
6) 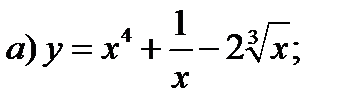
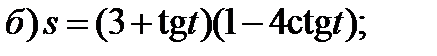
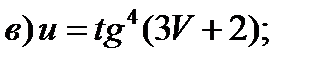
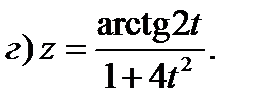
Задание 2. Составить уравнение касательной и нормали к кривой y=f(x) в точке с абсциссой х0.
1) 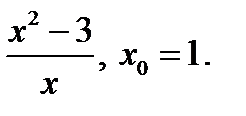
2) 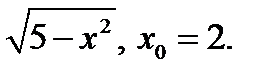
3) 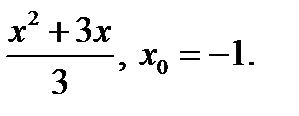
4) 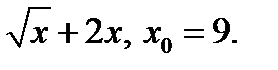
5) 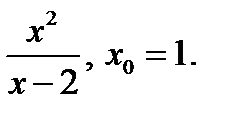
6) 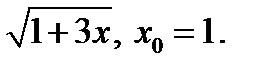
Задание 3. Найти производную 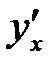 функции y=у(x), заданной параметрически:
функции y=у(x), заданной параметрически: 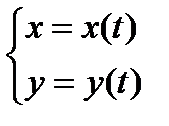
1) 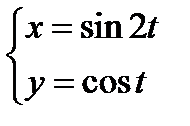
2) 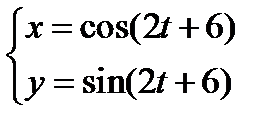
3) 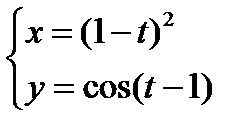
4) 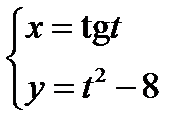
5) 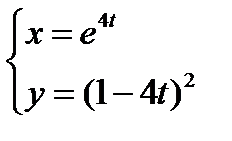
6) 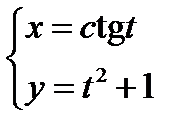
Задание 4. Найти дифференциалы функций:
1) 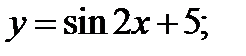
2) 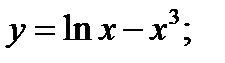
3) 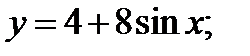
4) 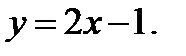
5) 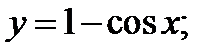
6) 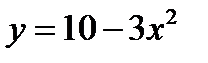
Задание 5. Найти производную функции логарифмическим дифференцированием
1) 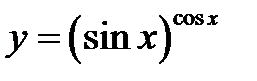
2) 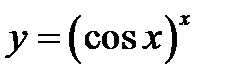
3) 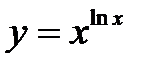
4) 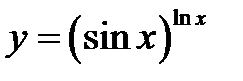
5) 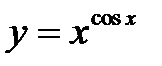
Задание 6 . Найти пределы, используя правило Лопиталя.
1) 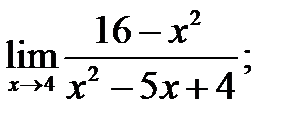
2) 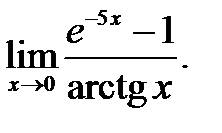
3) 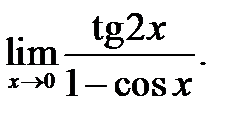
4) 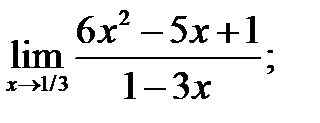
5) 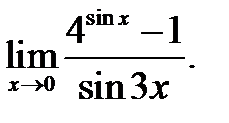
Практическое занятие. Нахождение неопределённого интеграла
Интегрирование по частям
 Интегрирование по частям ‒ приём, который применяется почти так же часто, как и замена переменной. Пусть u(x) и v(x) ‒ функции, имеющие непрерывные частные производные. Тогда по формуле дифференцирования произведения d(uv) = u∙dv + v∙du
Интегрирование по частям ‒ приём, который применяется почти так же часто, как и замена переменной. Пусть u(x) и v(x) ‒ функции, имеющие непрерывные частные производные. Тогда по формуле дифференцирования произведения d(uv) = u∙dv + v∙du 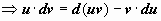 . Находим неопределённые интегралы для обеих частей этого равенства (при этом
. Находим неопределённые интегралы для обеих частей этого равенства (при этом 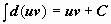 ):
):


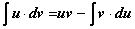 .
.
 Эта формула и называется формулой интегрирования по частям. Часто ее записывают в производных (dv = v’∙ dx , du = u’∙ dx):
Эта формула и называется формулой интегрирования по частям. Часто ее записывают в производных (dv = v’∙ dx , du = u’∙ dx):
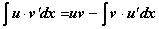 .
.
 Примеры:
Примеры: 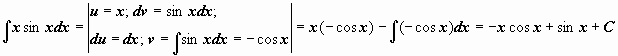 .
. 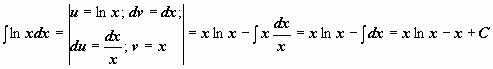 .
.
 Формула интегрирования по частям может применяться неоднократно. При наличии небольшого опыта в простых интегралах нет необходимости выписывать промежуточные выкладки (u = …, dv = …), можно сразу применять формулу, представив интеграл в виде
Формула интегрирования по частям может применяться неоднократно. При наличии небольшого опыта в простых интегралах нет необходимости выписывать промежуточные выкладки (u = …, dv = …), можно сразу применять формулу, представив интеграл в виде 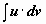 :
: 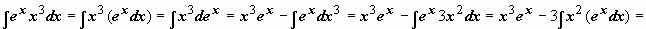
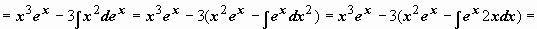
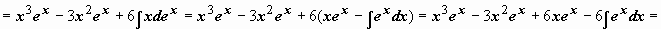
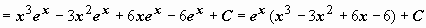 .
.
 Приведённые примеры показывают, для каких функций надо применять (или попытаться применить) формулу интегрирования по частям:
Приведённые примеры показывают, для каких функций надо применять (или попытаться применить) формулу интегрирования по частям:
 Интегралы вида
Интегралы вида 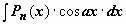 ,
, 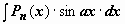 ,
, 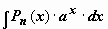 , где Pn(x) - многочлен n-ой степени. Так, для
, где Pn(x) - многочлен n-ой степени. Так, для 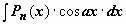 имеем
имеем 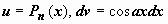 ,
, 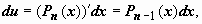
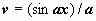 , и
, и 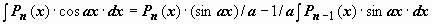 . В результате мы получили интеграл того же типа с многочленом степени на единицу меньше. После n-кратного применения формулы степень многочлена уменьшится до нуля, т.е. многочлен превратится в постоянную, и интеграл сведётся к табличному.
. В результате мы получили интеграл того же типа с многочленом степени на единицу меньше. После n-кратного применения формулы степень многочлена уменьшится до нуля, т.е. многочлен превратится в постоянную, и интеграл сведётся к табличному.
 Интегралы
Интегралы 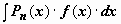 , где
, где 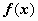 - трансцендентная функция, имеющая дробно-рациональную или дробно-иррациональную производную (ln x, arctg x, arcctg x, arcsin x, arcos x). В этом случае имеет смысл взять u = f(x), dv = Pn(x)dx, для того, чтобы в интеграле
- трансцендентная функция, имеющая дробно-рациональную или дробно-иррациональную производную (ln x, arctg x, arcctg x, arcsin x, arcos x). В этом случае имеет смысл взять u = f(x), dv = Pn(x)dx, для того, чтобы в интеграле 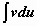 участвовала не f(x), а её производная. Пример:
участвовала не f(x), а её производная. Пример: 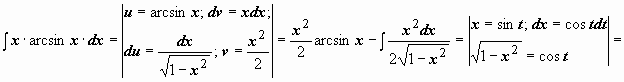
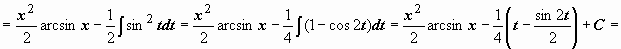
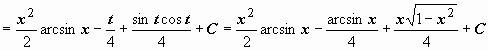 .
.
 Для некоторых функций применяется приём “сведения интеграла к самому себе”. С помощью интегрирования по частям (возможно, неоднократного) интеграл выражается через такой же интеграл; в результате получается уравнение относительно этого интеграла, решая которое, находим значение интеграла. Примеры:
Для некоторых функций применяется приём “сведения интеграла к самому себе”. С помощью интегрирования по частям (возможно, неоднократного) интеграл выражается через такой же интеграл; в результате получается уравнение относительно этого интеграла, решая которое, находим значение интеграла. Примеры:
 Найти
Найти 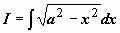 (это интеграл №19 из неопределённых интегралов; в предыдущем параграфе мы вычислили этот интеграл с помощью тригонометрической подстановки
(это интеграл №19 из неопределённых интегралов; в предыдущем параграфе мы вычислили этот интеграл с помощью тригонометрической подстановки 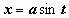 ).
). 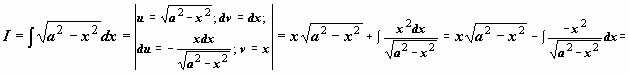
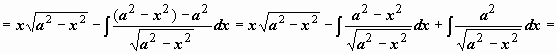
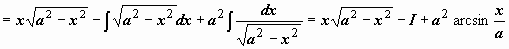 .
.
 В результате для искомого интеграла мы получили уравнение
В результате для искомого интеграла мы получили уравнение 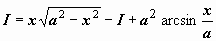 ,
,
решая которое, получаем 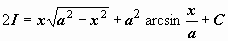 (константа С появилась вследствие того, что интегралы
(константа С появилась вследствие того, что интегралы 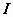 в правой и левой частях уравнения определены с точностью до произвольной постоянной) и
в правой и левой частях уравнения определены с точностью до произвольной постоянной) и 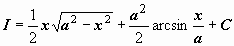 (константа
(константа 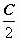 переобозначена через С).
переобозначена через С).
 Сведение интеграла к самому себе – самый простой способ нахождения часто встречающихся интегралов вида
Сведение интеграла к самому себе – самый простой способ нахождения часто встречающихся интегралов вида 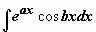 и
и 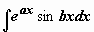 (
( 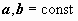 ). Например,
). Например,
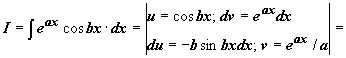
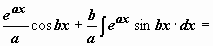
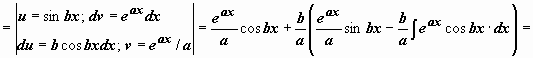
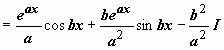 . Итак, после двукратного интегрирования по частям получено уравнение относительно
. Итак, после двукратного интегрирования по частям получено уравнение относительно 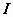 :
: 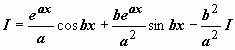 , решение которого
, решение которого 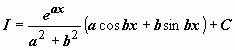 .
.
 При нахождении эти интегралов не принципиально, положим ли мы u = cos bx, dv = eax dx или u = eax, dv = cos bx dx; важно только при втором применении формулы интегрирования по частям загонять под знак дифференциала функцию того же типа, что и при первом (показательную или тригонометрическую).
При нахождении эти интегралов не принципиально, положим ли мы u = cos bx, dv = eax dx или u = eax, dv = cos bx dx; важно только при втором применении формулы интегрирования по частям загонять под знак дифференциала функцию того же типа, что и при первом (показательную или тригонометрическую).
Ещё один вид формул, которые обычно получаются с помощью интегрирования по частям, и используются для нахождения интегралов - рекуррентные соотношения. Если подынтегральная функция зависит от некоторого параметра n, и получено соотношение, которое выражает интеграл через аналогичный интеграл с меньшим значением n, то это соотношение и называется рекуррентным соотношением.
Примеры:
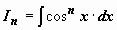 . Представим подынтегральную функцию в виде
. Представим подынтегральную функцию в виде 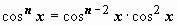
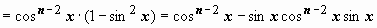 ; интеграл от первого слагаемого аналогичен исходному с значением параметра n на две единицы меньше; к интегралу от второго слагаемого применим формулу интегрирования по частям:
; интеграл от первого слагаемого аналогичен исходному с значением параметра n на две единицы меньше; к интегралу от второго слагаемого применим формулу интегрирования по частям:
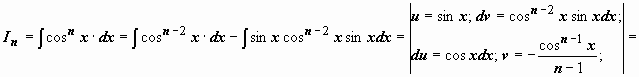
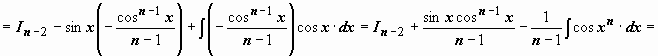
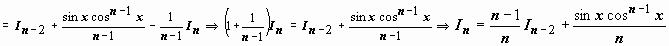 .
.
 Теперь, зная
Теперь, зная 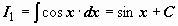 ,
, 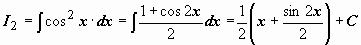 , мы можем выписать
, мы можем выписать 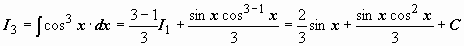 ;
; 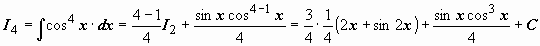 ;
;
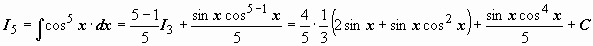

Практическое занятие. Вычисление определённого интеграла
Задания для практической работы
Задание 3. Вычислить определенные интегралы
а) 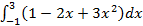 б)
б) 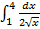 в)
в) 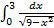
Задание 4. Вычислить определенные интегралы методом подстановки.
а) 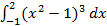
б). 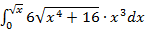
в) 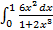
Задание 5. Вычислить площадь фигуры ограниченной линиями
1. 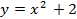
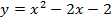

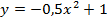
Задание 6. Решить задачу.
1.Скорость точки задана уравнением 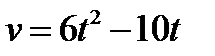 (м/с). Найти её путь за третью секунду движения.
(м/с). Найти её путь за третью секунду движения.
2.Скорость точки задана уравнением 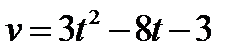 (м/с). Найти путь, пройденный телом за время от начала движения до остановки.
(м/с). Найти путь, пройденный телом за время от начала движения до остановки.
5. Методические рекомендации по выполнению и оформлению домашней контрольной работы
Контрольная работа по учебной дисциплине «Математика» для студентов заочной формы обучения составлена согласно учебному плану основной профессиональной образовательной программы среднего профессионального образования Государственного профессионального образовательного учреждения «Донецкий горный техникум им. Е.Т. Абакумова» по специальности 21.02.17 «Подземная разработка месторождений полезных ископаемых»
Задания контрольной работы охватывают все основные темы учебной программы. Контрольная работа выполняется студентом в тетради, где указывается номер варианта (задания студент выбирает из таблицы вариантов своей учебной группы), код (номера заданий, соответствующие варианту). Студент пользуется методическими указаниями для выполнения контрольной работы и указанной литературой, конспектом. Если студент применяет дополнительную литературу не указанную в списке, то необходимо в конце работы указать используемые источники, интернет-ресурсы и т.д.
Титульный лист заполняется согласно методическим требованиям, с которыми студент знакомится на установочной сессии.
Контрольная работа считается выполненной (выставляется оценка «зачтено»), если студент правильно решил и оформил более 80 % заданий. В противном случае работа возвращается студенту на доработку. Студент должен представить контрольную работу на проверку преподавателю в указанный срок, согласно учебному плану. В противном случае студент получает оценку «неудовлетворительно» и обязан выполнить контрольную работу заново.
Студент имеет право получить консультацию у преподавателя по графику консультаций, с которым может ознакомиться на заочном отделении или выяснить у преподавателя.
ТАБЛИЦА ВАРИАНТОВ
для выполнения контрольной работы
по учебной дисциплине «Математика»
для студентов заочной формы обучения специальности ЕН.01 «Математика»
для студентов заочной формы обучении я специальности
21.02.07 «Подземная разработка месторождений полезных ископаемы»
на основе среднего образования
Преподаватель: Левченко В.А.
Группа: 1ПР-17/з
| № варианта | ||||||||
Номера заданий
Примечание: номер варианта соответствует порядковому номеру ФИО студента контингента в журнале успеваемости.
ТАБЛИЦА ВАРИАНТОВ
для выполнения контрольной работы
по учебной дисциплине ЕН.01 «Математика»
для студентов заочной формы обучения специальности
21.02.07 «Подземная разработка месторождений полезных ископаемы»
на основе образовательно-квалифицированного уровня
квалифицированного рабочего
Преподаватель: Левченко В.А.
Группа: 1ПР-17/зту
| № варианта |
Номера заданий | |||||||
| 1 | 10 | 18 | 22 | 36 | 43 | 58 | 69 | 75 |
| 2 | 2 | 16 | 30 | 33 | 41 | 54 | 70 | 77 |
| 3 | 8 | 19 | 28 | 31 | 42 | 52 | 68 | 80 |
| 4 | 6 | 11 | 29 | 32 | 48 | 51 | 65 | 72 |
| 5 | 4 | 13 | 21 | 35 | 49 | 60 | 64 | 75 |
| 6 | 5 | 16 | 24 | 36 | 47 | 55 | 61 | 79 |
| 7 | 3 | 18 | 26 | 40 | 44 | 53 | 66 | 74 |
| 8 | 7 | 17 | 23 | 31 | 50 | 59 | 67 | 78 |
| 9 | 10 | 20 | 27 | 37 | 41 | 57 | 68 | 71 |
| 10 | 8 | 14 | 28 | 38 | 43 | 58 | 70 | 73 |
| 11 | 6 | 16 | 22 | 39 | 49 | 54 | 63 | 77 |
| 12 | 2 | 15 | 30 | 35 | 47 | 56 | 62 | 80 |
| 13 | 4 | 19 | 26 | 37 | 45 | 51 | 62 | 79 |
| 14 | 9 | 17 | 25 | 32 | 42 | 52 | 69 | 75 |
| 15 | 3 | 11 | 29 | 31 | 48 | 53 | 70 | 72 |
| 16 | 2 | 13 | 28 | 33 | 47 | 60 | 68 | 71 |
| 17 | 5 | 14 | 27 | 40 | 50 | 55 | 65 | 73 |
| 18 | 4 | 13 | 21 | 35 | 49 | 60 | 64 | 75 |
| 19 | 5 | 16 | 24 | 36 | 47 | 55 | 61 | 79 |
| 20 | 3 | 18 | 26 | 40 | 44 | 53 | 66 | 74 |
| 21 | 7 | 17 | 23 | 31 | 50 | 59 | 67 | 78 |
| 22 | 10 | 20 | 27 | 37 | 41 | 57 | 68 | 71 |
| 23 | 8 | 14 | 28 | 38 | 43 | 58 | 70 | 73 |
| 24 | 6 | 16 | 22 | 39 | 49 | 54 | 63 | 77 |
| 25 | 2 | 15 | 30 | 35 | 47 | 56 | 62 | 80 |
| 26 | 4 | 19 | 26 | 37 | 45 | 51 | 62 | 79 |
| 27 | 9 | 17 | 25 | 32 | 42 | 52 | 69 | 75 |
| 28 | 3 | 11 | 29 | 31 | 48 | 53 | 70 | 72 |
| 29 | 2 | 13 | 28 | 33 | 47 | 60 | 68 | 71 |
| 30 | 5 | 14 | 27 | 40 | 50 | 55 | 65 | 73 |
Примечание: номер варианта соответствует порядковому номеру ФИО студента контингента в журнале успеваемости.
Тема: Функции, область определения функции, предел функции
Задания 1-10. Найти область определения функции
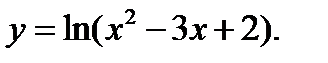
1.
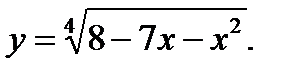
2.
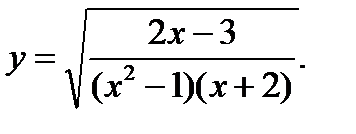
3.
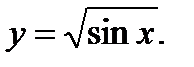
4.
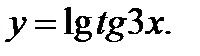
5.
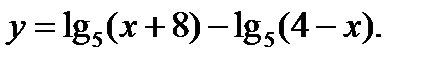
6.
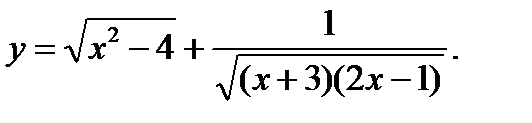
7.
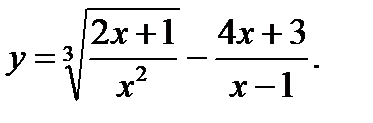
8.
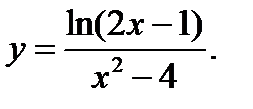
9.
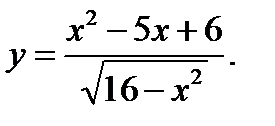
10.
Задания № 11-20. Найти предел функции
| 11. | 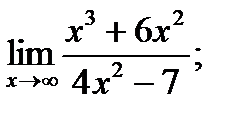 а) а)
| 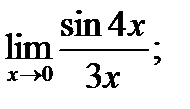 б) б)
|
| 12. | 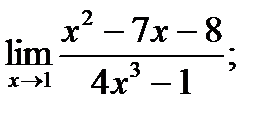 а) а)
| 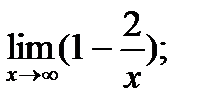 б) б)
|
| 13. | 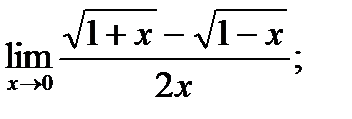 а) а)
| 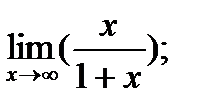 б) б)
|
| 14. | 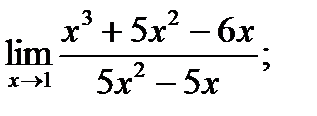 а) а)
| 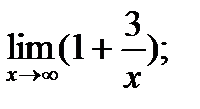 б) б)
|
| 15. | 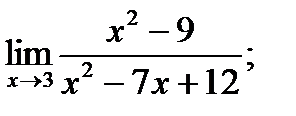 а) а)
| 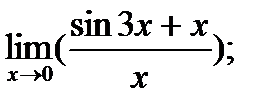 б) б)
|
| 16. | 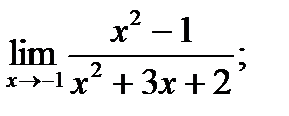 а) а)
| 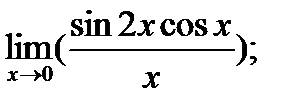 б) б)
|
| 17. | 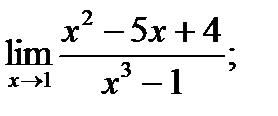 а) а)
| 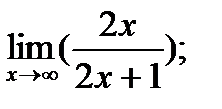 б) б)
|
| 18. | 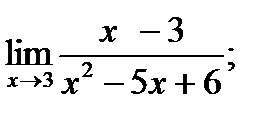 а) а)
| 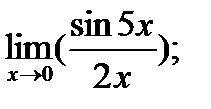 б) б)
|
| 19. | 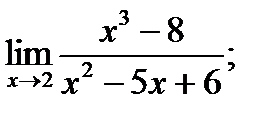 а) а)
| 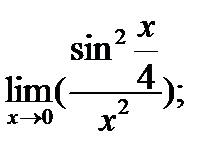 б) б)
|
| 20. | 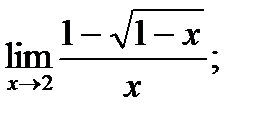 а) а)
| 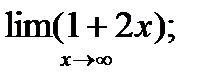 б) б)
|
Тема: Метод координат
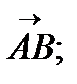 Задания № 21-30. В треугольнике с вершинами А(х1,, у1), В(х2,, у2) та С(х3, у3) найти:
Задания № 21-30. В треугольнике с вершинами А(х1,, у1), В(х2,, у2) та С(х3, у3) найти:
а) длину вектора
б) косинус внутреннего угла 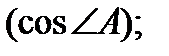
в) уравнение высоты, проведённой через вершину С;
г) уравнение медианы, которая проходит через вершину С;
д) выполнить рисунок.
21. А(0; 0) В(6; 3) С(3; 4)
22. А(1; -3) В(-5; 0) С(-2; 1)
23. А(-1; 1) В(5; 4) С(2; 5)
24. А(0; 0) В(6; 3) С(3; 4)
25. А(2; 2) В(-4; 5) С(-1; 6)
26. А(-1; -2) В(5; 1) С(2; 2)
27. А(-2; -1) В(4; 2) С(1; 3)
28. А(2; -1) В(-8; 4) С(-5; 5)
29. А(-1; -1) В(-7; 2) С(-4; 3)
30. А(3; -1) В(-3; 2) С(0; 3)
Задание № 31-40. Найти производную функции
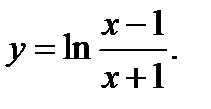
31.
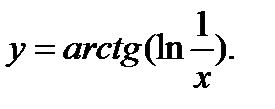
32.
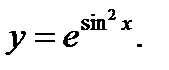
33.
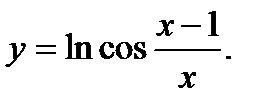
34.

35.
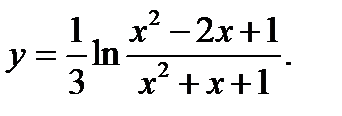
36.
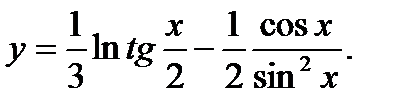
37.
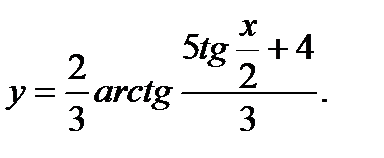
38.
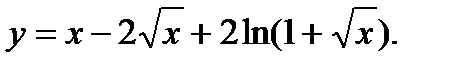
39.
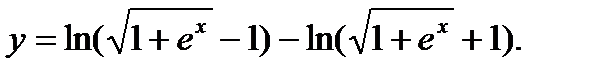
40.
Задания №41-50. Исследовать функцию и построить её график
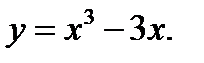
41.
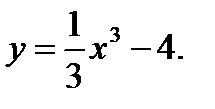
42.
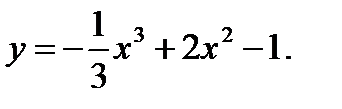
43.
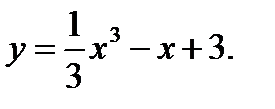
44.
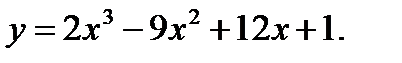
45.
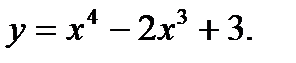
46.
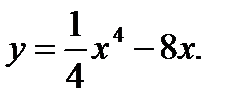
47.
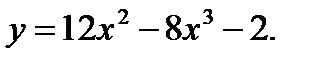
48.
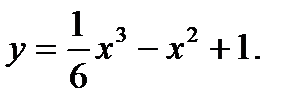
49.
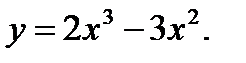
50.
Задание №51-60. Вычислить определённый интеграл
| 51. | 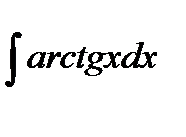 а) а)
| 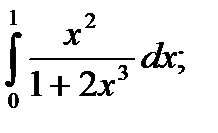 б) б)
|
| 52. | 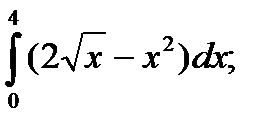 а) а)
| 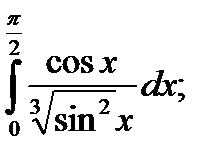 б) б)
|
| 53. | 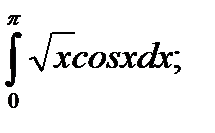 а) а)
| 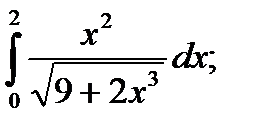 б) б)
|
| 54. | 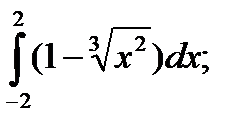 а) а)
| 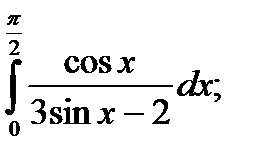 б) б)
|
| 55. | 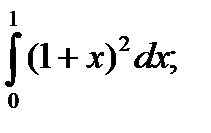 а) а)
| 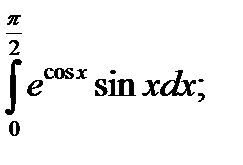 б) б)
|
| 56. | 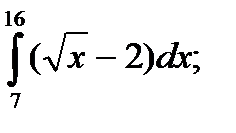 а) а)
| 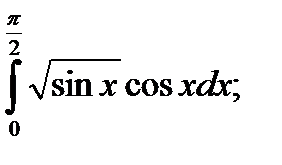 б) б)
|
| 57. | 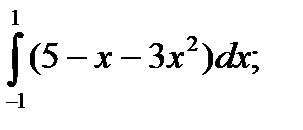 а) а)
| 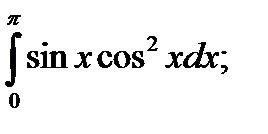 б) б)
|
| 58. | 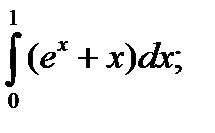 а) а)
| 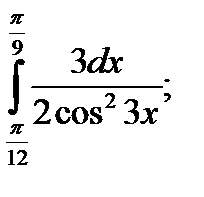 б) б)
|
| 59. | 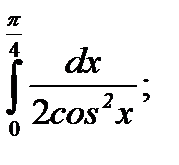 а) а)
| 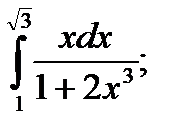 б) б)
|
| 60. | 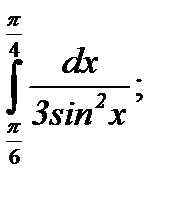 а) а)
| 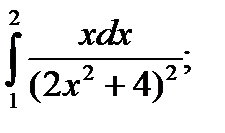 б) б)
|
Задание №61-70. Вычислить площадь фигуры, ограниченной линиями
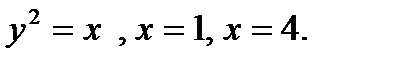
61.
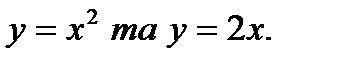
62.

63.
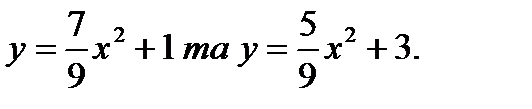
64.
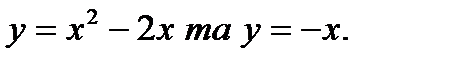
65.
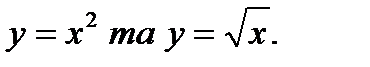
66.
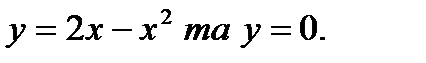
67.
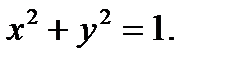
68.
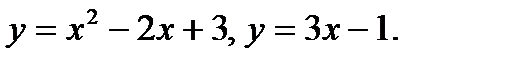
69.
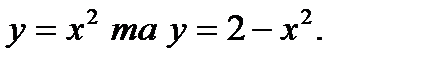
70.
Задание № 71-80. Задачи на классическое определение вероятности, применение формул комбинаторики для вычисления вероятности
Задание 71.
Какова вероятность того, что при бросании игрального кубика выпадает чётное число очков?
Задание 72.
В одном ящике находятся 8 белых и 12 красных шариков, в другом – 15 синих и 5 чёрных шариков. Из каждого ящика наугад вынимают по одному шарику, какова вероятность того, что вынули красный и чёрный шарики?
Задание 73.
В ящике лежат 20 одинаковых на ощупь шариков. Из них 12 белых и 8 чёрных. Наугад вынимают два шарика. Какова вероятность того, что оба шарика белые? Что они разного цвета?
Задание 74.
Из ящика, в котором находятся 4 шарика, пронумерованные числами 0, 1, 2, 3, наугад берут два шарика. Составить закон распределения суммы номеров двух вынутых шариков.
Задание 75.
При сборке прибора для точной подгонки определённой детали необходимо сделать несколько попыток. При этом деталь, забракованная при сборке одного прибора, уже используется при сборке других. Для установления количества деталей, которыми необходимо обеспечить рабочего, было проведено 100 наблюдений. Оказалось, что в 7 случаях понадобилась одна попытка, в 16 – две, в 55 – три, в 21 – четыре и в одном случае – пять попыток. Найти среднее количество деталей, необходимых для сборки одного прибора.
Задание 76.
Найти математическое ожидание Х, равной числу очков, которые выпадают на игральном кубике при одном броске.
Задание 77.
Подбросили два игральных кубика и подсчитали сумму выпавших очков. Что вероятнее получить в сумме: 7 или 8?
Задание 78.
В корзине находятся 4 белых и 7 чёрных шариков. Какова вероятность того, что наугад вынутый шарик окажется белого цвета?
Задание 79.
Подбросили две монеты. Какова вероятность того, что на каждой монете выпадет герб?
Задание 80.
Из полного набора костей домино наугад выбирается одна кость. Какова вероятность появления кости, сумма очков на которой равна шести?
Литература
Основная
1 Богомолов Н.В., Самойленко П.И. Математика. – М.: Дрофа, 2010.
2 Бродський Я.С., Павлов О.Л., Сліпенко А.К. Математика: Підручник. – К.: Вища школа., 2005
3 Бродський Я.С., Павлов О.Л., Сліпенко А.К. Дидактичні матеріали з математики: Навчальний посібник. – К.: Вища школа., 2005
4 Голованов Н.Н. Геометрическое моделирование. Учебник., М.: ФИЗМАТЛИТ, 2002
5 Валєєв К.Г., Джалладова І.А. Вища математика: Навч. посібник. У 2-х ч - К.: КНЕУ, 2001
6 Лопатько О.В. Математичні методи в розрахунках на ЕОМ: Навчальний посібник. – Львів: «Магнолія плюс», 2005
Дополнительная
1 В.М.Лейфура. Математика: Учебник для высших учебных учреждений І-ІІ уровней аккредитации – К.: Техника, 2003
2 Яковлев Г.М. Алгебра и начало анализа. Учебник ч І-ІІ - М.: Наука, 1987
3 Крамор в.С., Алгебра и начала анализа: Учебное пособие для вузов. – М.: Высшая школа, 2001.
4 Валуце І.І. Математика для техникумов. Учебник. – М.: Наука, 1987
5 Богомолов М.В. Практичні заняття з математики. Навчальний посібник. – К.: Вища школа, 1987
6 Зайцев И.Л. Элементы высшей математики для техникумов. Учебник. – М.: «Наука», 1982
Вариант № 5
Код 5, 15, 25, 35, 45, 55, 65, 75
Задание 5
Найти область определения функции
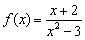
Решение: в числителе ничего особенного нет, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти «плохие» точки:
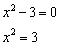
Полученное уравнение имеет два корня: 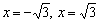 . Данные значения не входят в область определения функции. Действительно, подставьте
. Данные значения не входят в область определения функции. Действительно, подставьте 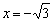 или
или 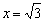 в функцию
в функцию 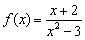 и вы увидите, что знаменатель обращается в ноль.
и вы увидите, что знаменатель обращается в ноль.
Ответ: область определения: 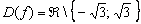
Задание 15
Найти предел функции 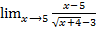
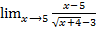 =
= 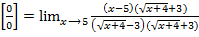 =
= 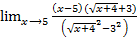 =
= 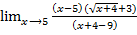 =
= 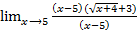 =
= 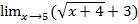 =3+3=6
=3+3=6
Задание 25
Дано: прямоугольный параллелепипед ABCDA1B1C1D1; DA=1; DC=2; DD1=3. Найти: угол между прямыми CB1 и D1B.
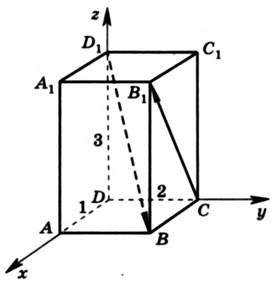
Рис. 1.
Решение
Введем систему координат Dxyz (см. рис. 1) и найдем направляющие векторы D1B и СB1. Для этого сначала найдем координаты точек D1, B, C и B1, так как через них проходят нужные нам прямые. D1(0;0;3), B(1;2;0), C(0;2;0), B1(1;2;3). Зная координаты точек, мы можем найти координаты направляющих векторов, вычитая из координат конца координаты начала вектора: 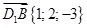 ,
, 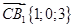 . Найдем косинус угла между прямыми CB1 и D1B:
. Найдем косинус угла между прямыми CB1 и D1B: 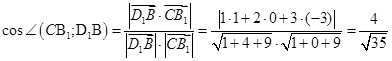 .
.
Значит, 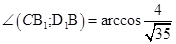 .
.
Задание 35
Найти производную функции 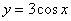
Решение
Смотрим в таблицу производных. Производная косинуса там есть, но у нас 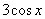 .
.
Решаем:
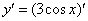
Самое время использовать правило, выносим постоянный множитель за знак производной:
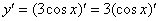
А теперь превращаем наш косинус по таблице:
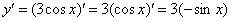
Ну и результат желательно немного «причесать» – ставим минус на первое место, заодно избавляясь от скобок:
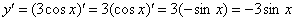
Задание 45
Исследовать функцию и построить график функции
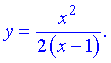
Решение:
1) Функция определена везде кроме точки, в которой знаменатель превращается в ноль ( 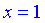 ). Область определения состоит из двух интервалов
). Область определения состоит из двух интервалов
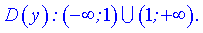
2) При подстановке значения 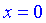 получим
получим
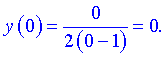
Такую же точку получим если приравняем функцию к нулю. Точка 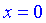 - единственная точка пересечения с осями координат.
- единственная точка пересечения с осями координат.
3) Проверяем функцию на четность
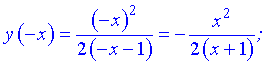
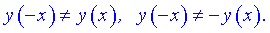
Итак функция ни четная, ни нечетная, непериодическая.
4) В данном случае имеем одну точку разрыва 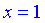 . Вычислим границы слева и справа от этой точки
. Вычислим границы слева и справа от этой точки
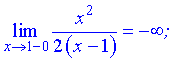
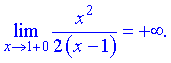
Итак 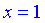 – точка разрыва второго рода.
– точка разрыва второго рода.
5) Для отыскания интервалов монотонности вычисляем первую производную функции
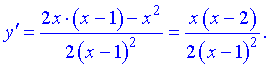
Приравнивая ее к нулю получим точки подозрительные на экстремум 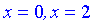 . Они разбивают область определения на следующие интервалы монотонности
. Они разбивают область определения на следующие интервалы монотонности
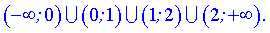
Исследуем поведение производной слева и справа от найденных точек разбиения
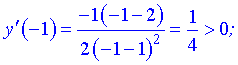
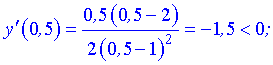
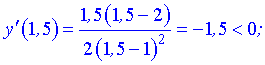
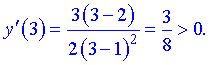
Графически интервалы монотонности будут иметь вид
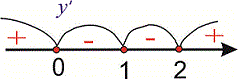
Исследуемая функция возрастает на интервалах 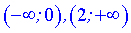 и убывает
и убывает 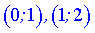 .
.
Точка 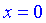 – точка локального максимума,
– точка локального максимума, 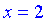 – локального минимума. Найдем значение функции
– локального минимума. Найдем значение функции
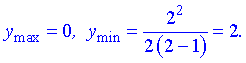
6) Для отыскания интервалов выпуклости найдем вторую производную
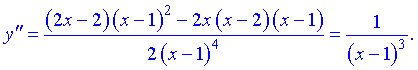
Таких интервалов нет, поскольку вторая производная не принимает нулевых значений в области определения.
7) Точка 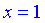 – вертикальная асимптота функции. Уравнение наклонной асимптоты имеет вид
– вертикальная асимптота функции. Уравнение наклонной асимптоты имеет вид
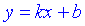
где 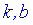 - границы которые вычисляются по правилу
- границы которые вычисляются по правилу
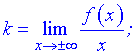
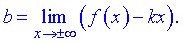
Находим нужные границы
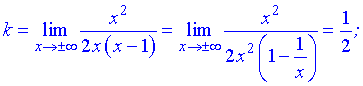
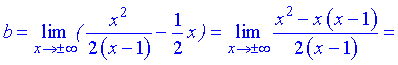
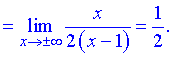
Конечный вид прямой следующий
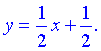
8) На основе проведенного анализа выполняем построение графика функции. Для этого сначала строим вертикальные и наклонные асимптоты, затем находим значение функции в нескольких точках и по них проводим построение.
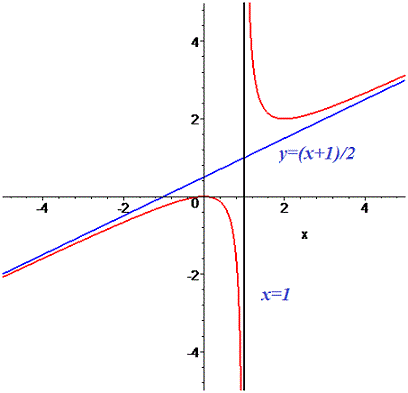
--------------------------------------
Задание 55
Вычислить определённый интеграл
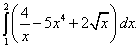
Используя свойства определённого интеграла, а при нахождении первообразных – табличные интегралы получим
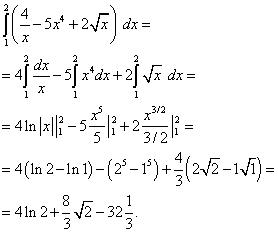
Задание 65
Найти площадь фигуры, ограниченной линиями 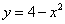 ,
, 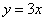 ,
, 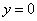 и находящейся в 1-й четверти.
и находящейся в 1-й четверти.
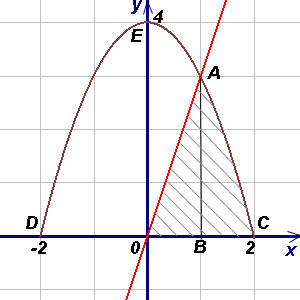
Решение
Чтобы воспользоваться формулой (1), представим площадь искомой фигуры в виде суммы площадей треугольника OAB и криволинейной трапеции ABC. При вычислении площади треугольника OAB пределами интегрирования служат абсциссы точек O и A, а для фигуры ABC - абсциссы точек A и C (A является точкой пересечения прямой OA и параболы, а C - точкой пересечения параболы с осью Ox). Решая совместно (как систему) уравнения прямой и параболы, получим 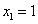 (абсциссу точки A) и
(абсциссу точки A) и 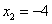 (абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично получим
(абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично получим 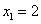 ,
, 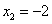 (абсциссы точек C и D). Таким образом имеем всё для нахождения площади фигуры. Находим:
(абсциссы точек C и D). Таким образом имеем всё для нахождения площади фигуры. Находим:
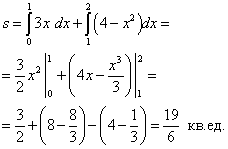
Задание 75
Конференция длится три дня. В первый и второй день выступают по 15 докладчиков, в третий день – 20. Какова вероятность того, что доклад профессора Морозова выпадет на третий день, если порядок докладов определяется жеребьевкой?
Решение
Что здесь является элементарным исходом? – Присвоение докладу профессора какого-то одного из всех возможных порядковых номеров для выступления. В жеребьевке участвует 15+15+20=50 человек. Таким образом, доклад профессора Морозова может получить один из 50 номеров. Значит, и элементарных исходов всего 50.
А какие исходы благоприятные? – Те, при которых окажется, что профессор будет выступать в третий день. То есть, последние 20 номеров.
По формуле вероятность P(A)= 20/50=2/5=4/10=0,4
Ответ: 0,4
Таблица перевода баллов в оценку
| Количество набранных баллов | Оценка |
| 61-80 | зачтено |
| меньше 61 | не зачтено |
Максимальное количество баллов за задание – 10, студент получает, когда правильно решил задачу, дал пояснения, записал ответ, придерживался математической культуры записи.
7-9 баллов – студент получает, когда решил задание, однако объяснение содержит неточности или неполное, допустил незначительные ошибки в вычислениях.
4-6 баллов – студент получает, если ход решения задачи правильных, однако нет объяснения, допущены ошибки в вычислениях.
Меньше 4 баллов – студент получает, если задание выполнено не правильно, однако выдержаны некоторые этапы решения, не дано объяснения хода решения, ответ получен не правильный.
КРИТЕРИИ ОЦЕНИВАНИЯ
по учебной дисциплине ЕН.01 Математика
«5» (отлично) – за глубокое и полное овладение содержанием учебного материала, в котором студент легко ориентируется; научно-понятийным аппаратом; за умение практически применять теоретические знания, качественно выполнять все виды работ, высказывать и обосновывать свои суждения. Отличная отметка предполагает грамотное и логичное изложение ответа (в письменной форме) на практико-ориентированные вопросы, обоснование своего высказывания с точки зрения известных теоретических положений.
«4» (хорошо) – если студент полно освоил учебный материал, владеет научно-понятийным аппаратом, ориентируется в изученном материале, осознанно применяет знания на практике, грамотно излагает ответ (в письменной форме), но содержание и форма ответа имеют отдельные неточности.
«3» (удовлетворительно) – если студент обнаруживает знание и понимание основных положений учебного материала, но излагает его неполно, непоследовательно, допускает неточности в определении понятий, в применении теоретических знаний при ответе на практико-ориентированные вопросы; не умеет доказательно обосновать свои суждения.
«2» (неудовлетворительно) – если студент имеет разрозненные, бессистемные знания по дисциплине, допускает ошибки в определении базовых понятий, искажает их смысл; не может практически применять теоретические знания.
Литература
1. Богомолов Н.В., Математика: учебное пособие для ссузов. – М.: Дрофа, 2010
2. Бродский Я.С., Павлов А.Л., Слипенко А.К., Математика: Учебник.-
К.:Высшая школа.,2005
3. Бродский Я.С., Павлов А.Л., Слипенко А.К. Дидактические материалы по математике: Учебное пособие.- К.: Высшая школа.,2005
4. Валеев К.Г., Джаллатова И.А. Высшая математика: Учеб. пособие. в 2-х ч - К.:КНЭУ,2001
5. Лейфура В.М. Математика: Учебник для студентов эконом. Специальностей вуз. учеб. заведений I-II уровней аккредитации - К.:Техника, 2003
6. Алгебра и начало анализа. ч II под. ред. Яковлева Г.М. –М.:наука,1987
7. Геометрия. Под. Ред. Яковлева Г.М. –М.: наука, 1988
8 . Математика для техникумов. под. ред. Валуце И.И –М.: Наука, 1989
Интернет- ресурсы:
1. http://en.edu.ru - естественно-научный портал
2. http://www.bestlibrary.ru - On–line библиотека
3. http://www.km.ru/literature/ - электронная библиотека LIB.KM.ru
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
по организации самостоятельной работы
студентов заочного отделения
ЕН.01Математика
по специальности 21.02.17
«Подземная разработка месторождений полезных ископаемых»
Разработал преподаватель Левченко В.А.
2019
Методические рекомендации предназначены для организации самостоятельной работы студентов заочного отделения специальности 21.02.17 «Подземная разработка месторождений полезных ископаемых» на основе среднего образования на основе образовательно-квалифицированного уровня квалифицированного рабочего по дисциплине ЕН.01 Математика.
Содержание
| Пояснительная записка | 4 |
| Тематический план для специальности 21.02.17 на основе среднего образования | 5 |
| Тематический план для специальности 21.02.17 на основе образовательно-квалифицированного уровня квалифицированного рабочего | 6 |
| Содержание программы и рекомендации к её самостоятельному изучению | 7 |
| Перечень и содержание практических занятий | 17 |
| Методические рекомендации по выполнению и оформлению домашней контрольной работы | 62 |
| Таблица вариантов с кодами заданий для специальности 21.02.17 на основе среднего образования | 63 |
| Таблица вариантов с кодами заданий для специальности 21.02.17 на основе образовательно-квалифицированного уровня квалифицированного рабочего | 64 |
| Образец выполнения домашней контрольной работы | 74 |
| Критерии оценивания выполнения домашней работы | 81 |
| Перечень экзаменационных вопросов | 82 |
| Критерии оценивания знаний по дисциплине | 84 |
| Литература | 85 |
1. Пояснительная записка
Программа учебной дисциплины ЕН.01 Математика предназначена для изучения в образовательных учреждениях среднего профессионального образования, при подготовке специалистов среднего звена.
Дисциплина ЕН.01 Математика относится к дисциплинам математического и естественнонаучного цикла подготовки специалистов среднего звена.
Для студентов специальности 21.02.17 «Подземная разработка месторождений полезных ископаемых» на основе среднего образования на освоение учебной дисциплины отведено 94 часа.
Для студентов специальности 21.02.17 «Подземная разработка меторождений полезных ископаемых» на образовательно-квалифицированного уровня квалифицированного рабочего на освоение учебной дисциплины отведено 72 часа.
В результате изучения учебной дисциплины студенты должны:
уметь:
- решать прикладные задачи в области профессиональной деятельности;
знать:
- значение математики в профессиональной деятельности и при освоении профессиональной подготовки специалистов среднего звена;
- основные математические методы решения прикладных задач в области профессиональной деятельности;
основные понятия и методы:
- математического анализа;
- линейной алгебры;
- теории комплексных чисел;
- теории вероятностей и математической статистики;
- основы интегрального и дифференциального исчисления.
Содержание дисциплины должно быть ориентировано на использовании и применении математического аппарата в специальных дисциплинах, подготовки курсовых и расчётных работ.
Базовыми дисциплинами для изучения дисциплины ЕН.01 Математика являются учебные дисциплины «Алгебра и начала математического анализа», «Геометрия».
В методических рекомендациях по изучению учебной дисциплины ЕН.01Математика приведены тематические учебные планы для специальности 21.02.17 «Подземная разработка месторождений полезных ископаемых» на основе среднего образования и на основе образовательно-квалифицированного уровня квалифицированного рабочего.
ТЕМАТИЧЕСКИЙ ПЛАН
учебной дисциплины ЕН.01 Математика
для заочной формы обучения
специальности 21.02.17
«Подземная разработка месторождений полезных ископаемых»
на основе среднего образования
| № п/п |
Наименование раздела и темы
Количество часов
всего по учебному плану
Аудитор.
Занятий
В том числе
самост.
Работа
Итого:
ТЕМАТИЧЕСКИЙ ПЛАН
учебной дисциплины ЕН.01 Математика
для заочной формы обучения
специальности 21.02.17
«Подземная разработка месторождений полезных ископаемых»
на основе образовательно-квалифицированного уровня
квалифицированного рабочего
| № п/п |
Наименование раздела и темы
Количество часов
всего по учебному плану
Аудитор.
Занятий
В том числе
самост.
Работа
Итого:
3. Содержание программы и рекомендации к её самостоятельному изучению
Раздел 1. Элементы линейной алгебры
Дата: 2019-11-01, просмотров: 354.