Понятие об определённом интеграле. Формула Ньютона-Лейбница. Пределы интегрирования. Историческая справка «Основоположники дифференциального и интегрального исчисления». Алгоритм нахождения определённого интеграла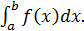 
Основные свойства неопределённого интеграла. Вычисление определённого интеграла: непосредственное интегрирование, методом замены переменной (методом подстановки), интегрирование по частям.
Практическое занятие. Вычисление определённого интеграла
Вопросы для самопроверки:
1. Выпишите формулу Ньютона-Лейбница?
2. Понятие верхнего и нижнего предела интегрирования.
3. Почему формулу вычисления определённого интеграла называют формулой Ньютона-Лейбница?
4. Приведите основные свойства определённого интеграла.
5. В чём заключается суть метода вычисления определённого интеграла методом замены переменной (методом подстановки)?
6. В чём заключается суть метода вычисления определённого интеграла по частям?
Тема 6.3 Геометрическое и физическое приложение определённого интеграла
Геометрический смысл определённого интеграла. Геометрические приложения определённого интеграла. Вычисление площадей плоских фигур, площади криволинейной трапеции с помощью определённого интеграла. Вычисление объёмов тел вращения с помощью определённого интеграла.
Физическое приложение определённого интеграла: вычисление пути, пройденного точкой, вычисление работы переменной силы.
Практическое занятие. Вычисление площади криволинейной трапеции и объёмов тел вращения с помощью определённого интеграла.
Вопросы для самопроверки:
1. В чём заключается геометрический смысл определённого интеграла?
2. Как вычислить площадь криволинейной трапеции с помощью определённого интеграла? Рассмотрите все случаи расположения криволинейной трапеции в системе координат.
3. Как вычислить объём тела вращения с помощью определённого интеграла?
4. В чём заключается механический (физический) смысл определённого интеграла?
5. В чём отличие определённого интеграла от неопределённого.
Перечень практических занятий
Практическое занятие. Операции с матрицами. Вычисление определителей второго и третьего порядка.
Практическое занятие. Решение систем линейных уравнений.
Практическое занятие. Операции над комплексными числами. Приложения комплексных чисел.
Практическое занятие. Нахождение вероятности.
Практическое занятие. Нахождение математического ожидания дискретной случайной величины.
Практическое занятие. Вычисление пределов.
Практическое занятие. Исследование функций на непрерывность.
Практическое занятие. Нахождение производной.
Практическое занятие. Нахождение неопределённого интеграла.
Практическое занятие. Вычисление определённого интеграла.
Практическое занятие. Вычисление площади криволинейной трапеции и объёмов тел вращения с помощью определённого интеграла. Приложение определённого интеграла.
Практическое занятие. Операции с матрицами. Вычисление определителей второго и третьего порядка.
Цель. освоить способы выполнения операций над матрицами, элементарные преобразования матриц, вычисление определителя, нахождение обратной матрицы
Решение заданий
Задание 1.
Пусть
.
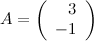Найти матрицу
.
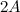Решение.
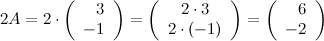
Ответ.
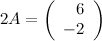
Задание 2.
Найти
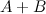, если
, 
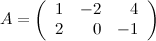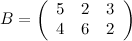
Решение.
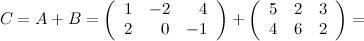
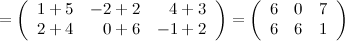
Ответ
. 
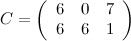
Задание 3. Найти матрицу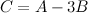 
,
если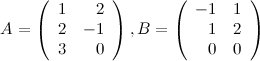 
Решение.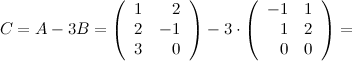 
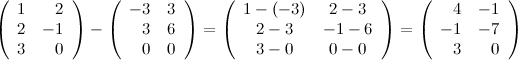
Ответ.
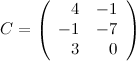
Задание 4. Вычислить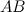 
и 
,
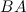если
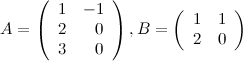
Решение. Так как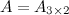 
, а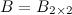 
, то произведение возможно и результатом операции умножения будет матрица 
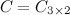, а это матрица вида 
.
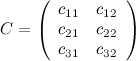Вычислим элементы матрицы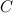 
:
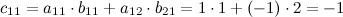
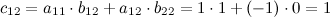
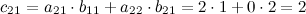
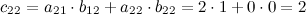
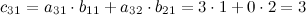
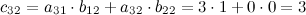
Итак,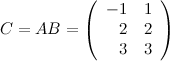 
.
Выполним произведения в более компактном виде:
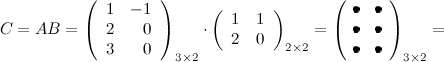
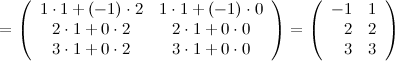
Найдем теперь произведение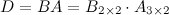 
. Так как количество столбцов матрицы 
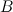(первый сомножитель) не совпадает с количеством строк матрицы 
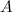(второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ.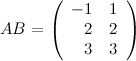 
. В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы 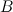не совпадает с количеством строк матрицы .
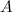Задание 5. Найти матрицу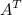 
, если
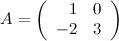
Решение.
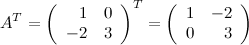
Ответ.
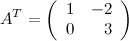
Задание 6. Найти минор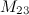 
к элементу 
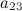определителя
.
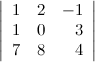Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
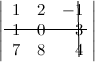
тогда
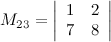
Ответ.
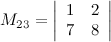
Задание 7. Найти алгебраическое дополнение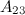 
к элементу 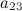определителя
.
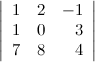Решение.
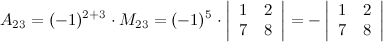
Ответ.
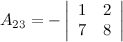
Задание 8. Вычислить определитель матрицы.
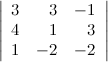
Решение.
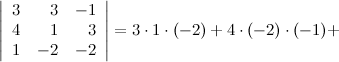
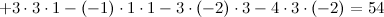
Ответ.
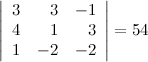
Задание 9. Найти обратную матрицу к матрице
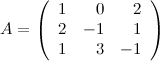
Решение. Вычисляем определитель матрицы:
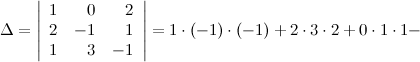
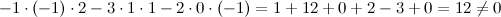
Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица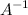 
к матрице 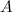находится по формуле:
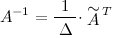
Найдем союзную матрицу 
, для этого вычислим алгебраические дополнения к элементам матрицы :
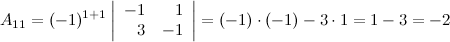
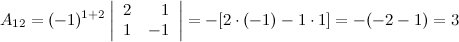
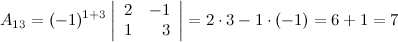
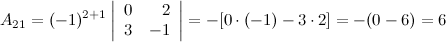
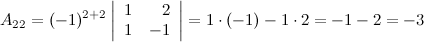
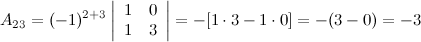
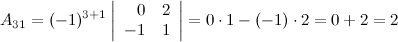
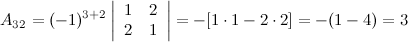
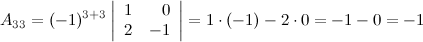
Таким образом,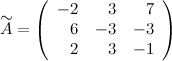 
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
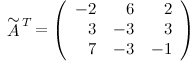
Итак,
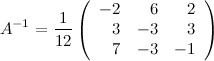
Ответ.
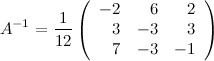
Практическое занятие. Решение систем линейных уравнений.
Цель. Формировать умение исследовать и использовать различные методы для решения систем линейных алгебраических уравнений.
Решение задач
Справочный материал и примеры.
Рассмотрим системы линейных алгебраических уравнений (СЛАУ) произвольной размерности, состоящие из m уравнений с n неизвестными:
. (*)
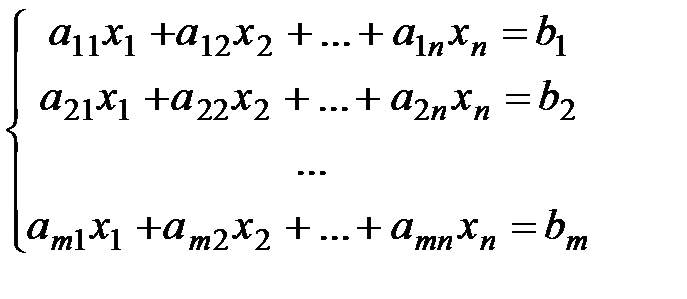Матрица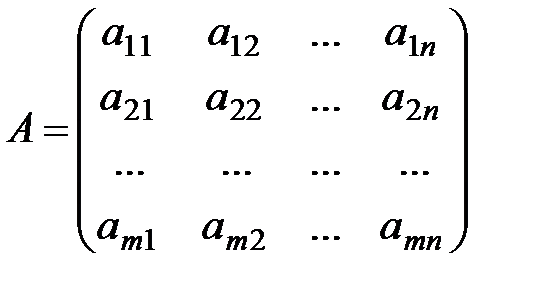 
, составленная из коэффициентов системы (*), называется матрицей системы (ее размер – mxn), а вектор 
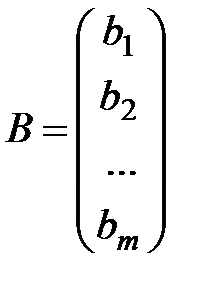(m-мерный)- столбцом (вектором) свободных членов. Матрицу вида 
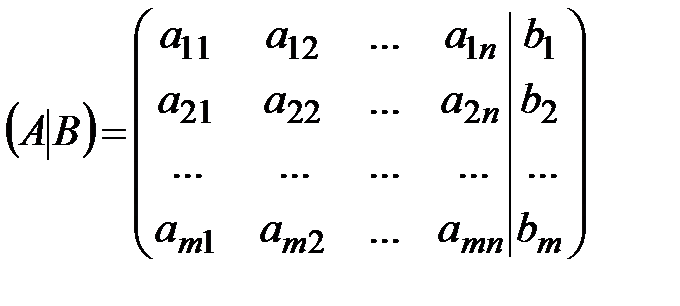называют расширенной матрицей системы (*). Любой набор значений неизвестных 
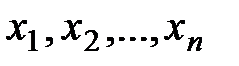, образующих n-мерный вектор 
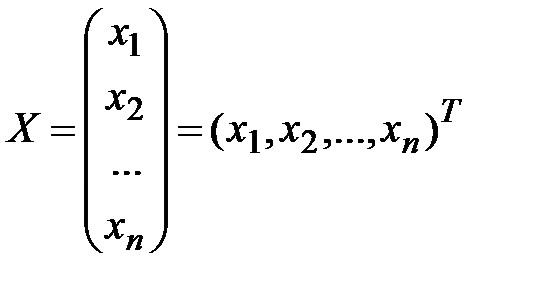, является решением системы (*), если эти числа удовлетворяют всем уравнениям системы (т.е. превращают их в тождества). Очевидно, что 
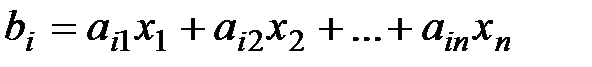при каждом i=1,2,…,m (i-е уравнение представляет собой скалярное произведение i-й строки матрицы системы на вектор X), и (*) можно переписать в виде
. (**)
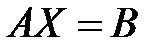Запись (**) называется "матричной (векторной) формой записи" системы (*).
Пример 1. Выписать матрицу коэффициентов и столбец свободных членов для СЛАУ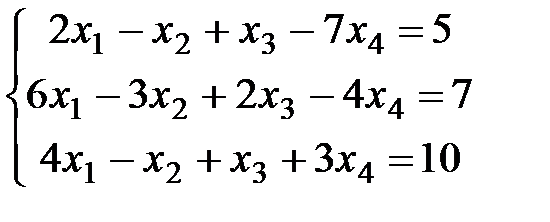 
.
Решение. Очевидно, что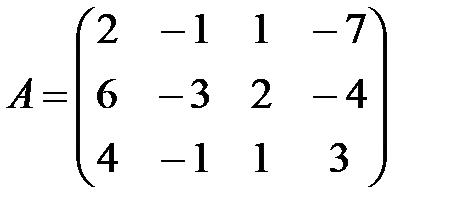 
; 
.
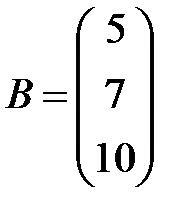Пример 2. Записать СЛАУ, если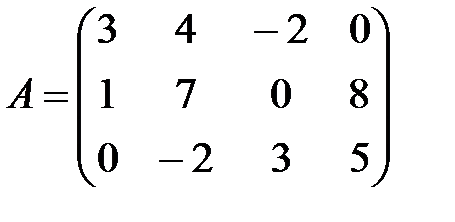 
, 
.
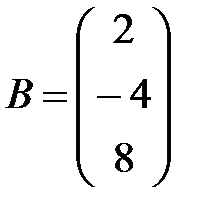Решение. Введем в рассмотрение вектор X и с каждым столбцом мысленно сопоставим неизвестное: с первым столбцом -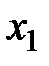 
, со вторым - 
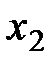, с третьим - 
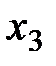, с четвертым - 
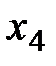. Окончательно нужная система линейных алгебраических уравнений имеет вид
.
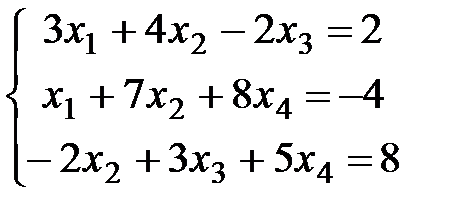Классификация систем линейных алгебраических уравнений. Определения и основные теоремы. Если СЛАУ (*) имеет, хотя бы одно решение, она называется совместной (соответственно, система несовместная, если она вообще не имеет решений). Совместная система (*) называется определенной, если она имеет единственное решение, и неопределенной, если имеет более одного решения (в последнем случае у нее бесконечно много решений).
Матрицу системы (*) будем называть приведенной (а саму систему канонической), если в каждой i-й строке (i=1,2,…,m) есть элемент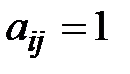 
, а все остальные элементы j-го cтолбца равны нулю. Такие элементы (и соответствующие им неизвестные) будем называть ведущими, а оставшиеся неизвестные назовем свободными.
Теорема 1 (Кронекера-Капелли). СЛАУ (*) совместна тогда и только тогда, когда ранг матрицы системы совпадает с рангом ее расширенной матрицы, т.е выполняется равенство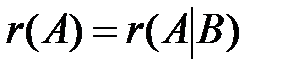 
.
Для совместной системы число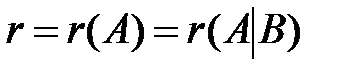 
назовем рангом системы.
Теорема 2 (о количестве решений). Пусть СЛАУ (*) совместна. Если ее ранг равен числу неизвестных (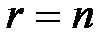 
), то система является определенной; если ранг системы меньше числа неизвестных ( 
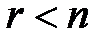), то исходная система – неопределенная.
Неопределенная система, как было отмечено, имеет бесконечное множество решений. Совокупность всех решений называется общим решением системы.
Алгоритм метода Гаусса. Цель рассуждений – путем элементарных преобразований свести исходную систему к равносильной, решение которой можно выписать непосредственно. Основными шагами метода Гаусса являются следующие.
I. Прямой ход. Выписать расширенную матрицу системы, путем элементарных преобразований свести ее к эквивалентной ступенчатой и определить ранги матрицы и расширенной матрицы системы. Если они различны, то исходная система несовместна, т.е. не имеет решений. Если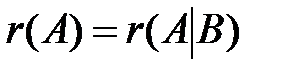 
, то переходим к следующему этапу.
II. Сравнить ранг системы и число неизвестных, сделать вывод о количестве решений, учитывая теорему 2.
III. Обратный ход. Ступенчатую матрицу преобразовать к эквивалентной ей приведенной. Определить, какие неизвестные являются ведущими, какие – свободными.
IV. Выписать по полученной матрице систему, записать ответ (выразив, в случае неопределенной системы, ведущие элементы через свободные для построения общего решения).
Пример 3. Решить СЛАУ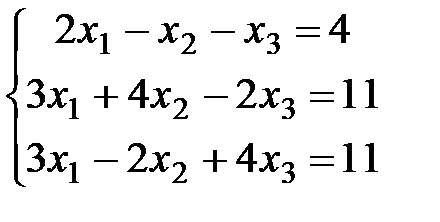 
.
Решение. Преобразуем расширенную матрицу системы:
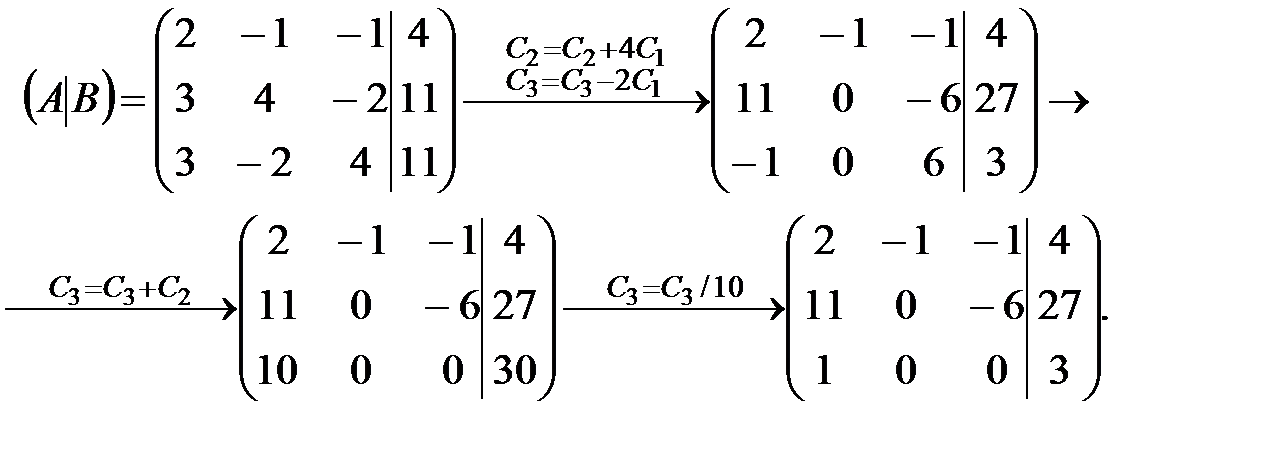
Последняя матрица – ступенчатая. Ведущими неизвестными для нее являются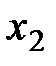 
в первой строке, 
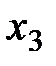во второй и 
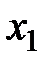в третьей. Очевидно, что система совместна и ее ранг равен 3: 
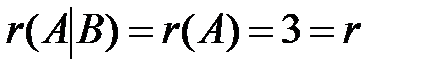. Поскольку число неизвестных также равно 3, исходная система является определенной.
Переходим к проведению преобразований по обратному методу Гаусса (теперь необходимо получать нули НАД ведущими элементами).
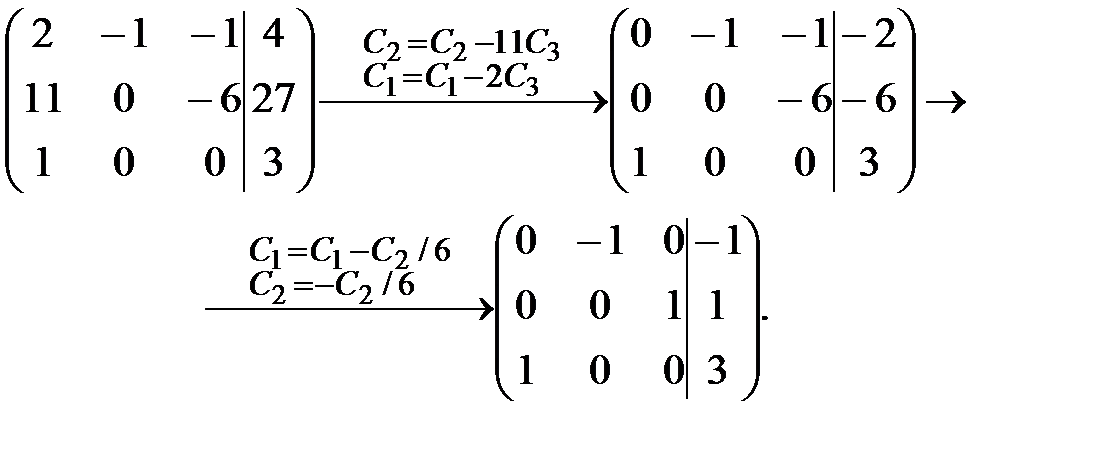
Теперь составляем по последней матрице систему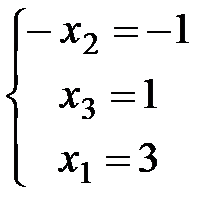 
и выписываем значения неизвестных в порядке их номеров: X=(3;1;1)T. Это и есть ответ.
Пример 4. Для СЛАУ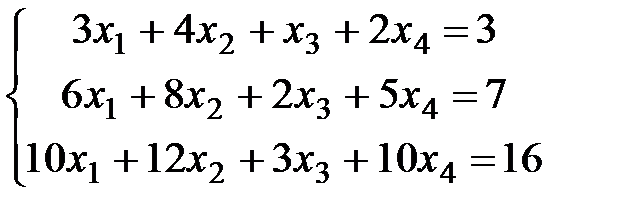 
найти общее и два частных решения.
Решение. Приведем расширенную матрицу системы к ступенчатой.
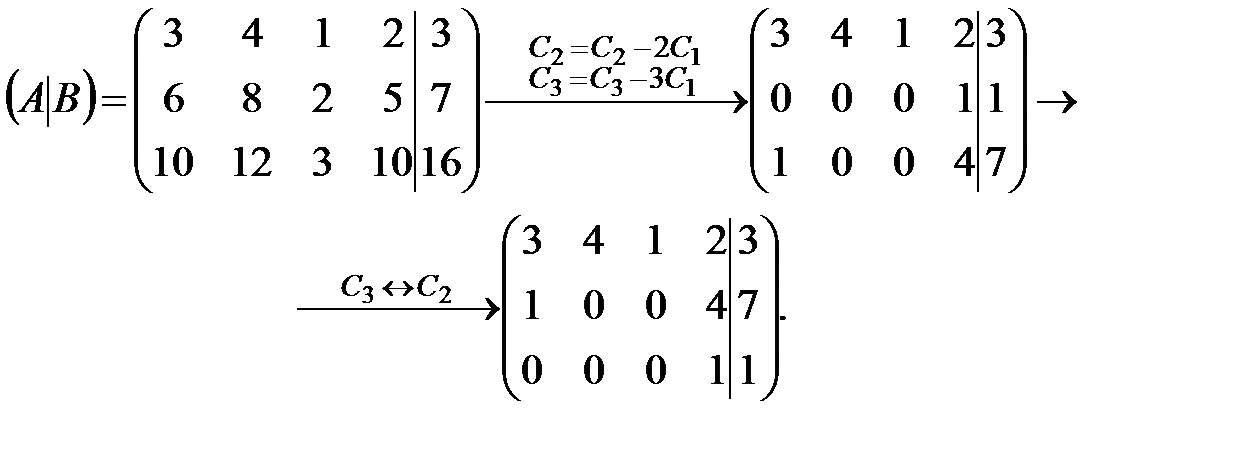
Очевидно, что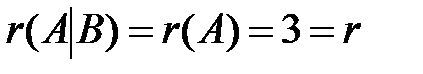 
, число неизвестных n=4 и в соответствии с теоремой 6.2 исходная система является неопределенной. Ведущие неизвестные: 
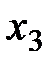в первой строке, 
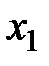во второй, 
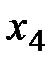в третьей. Свободное неизвестное - 
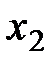. Обратным ходом преобразуем матрицу к приведенному виду:
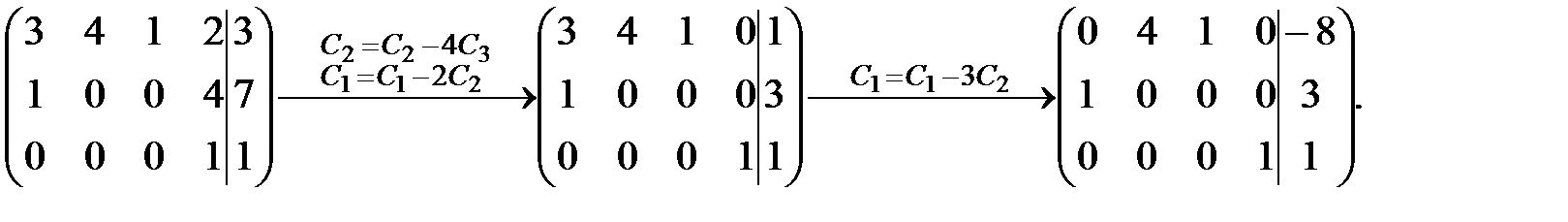
Выписываем полученную систему и ведущие неизвестные выражаем через свободные: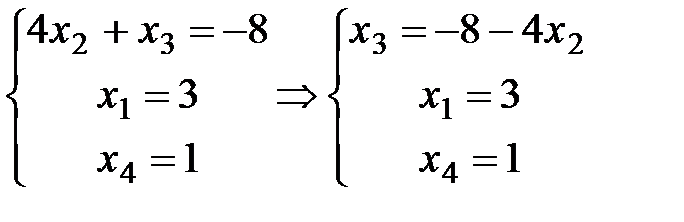 
. Общее решение записываем в порядке нумерации неизвестных: 
, 
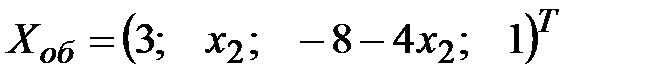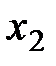- любое вещественное число.
Частное решение можно получить, если придать свободному неизвестному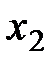 
конкретное числовое значение. Например, при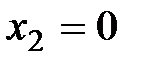 
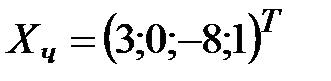, а при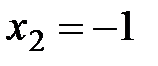 
.
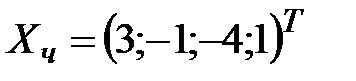Теорема Крамера. Рассмотрим «квадратную» систему линейных уравнений (число неизвестных совпадает с числом уравнений) вида
. (*)
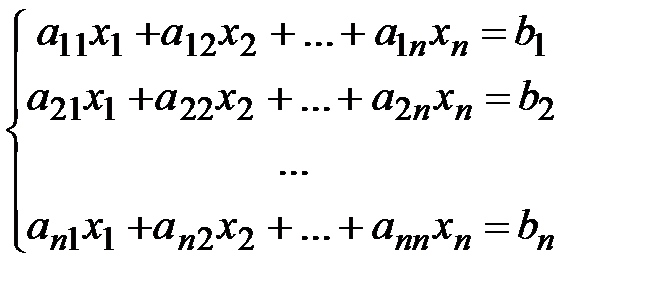Теорема 3 (теорема Крамера). Если определитель матрицы системы (*) отличен от нуля (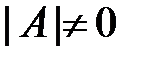 
), то данная система имеет единственное решение, причем значения неизвестных находятся по формулам
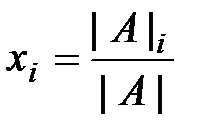, i=1,2,…,n
где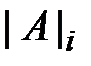 
- определитель матрицы, полученной из исходной матрицы системы путем замены i-го столбца на столбец свободных членов.
Пример 5. Решить систему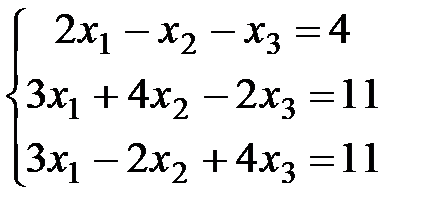 
методом Крамера.
Решение. Выписываем A - матрицу системы и B - столбец свободных членов: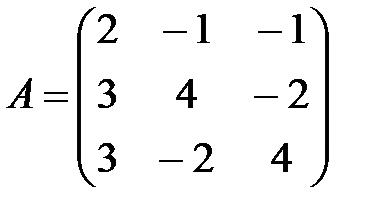 
, 
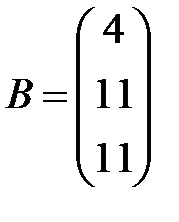. Далее вычисляем определители:
;
;
;
.
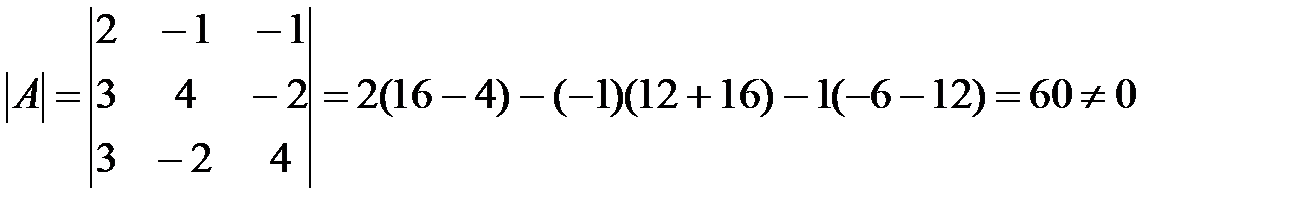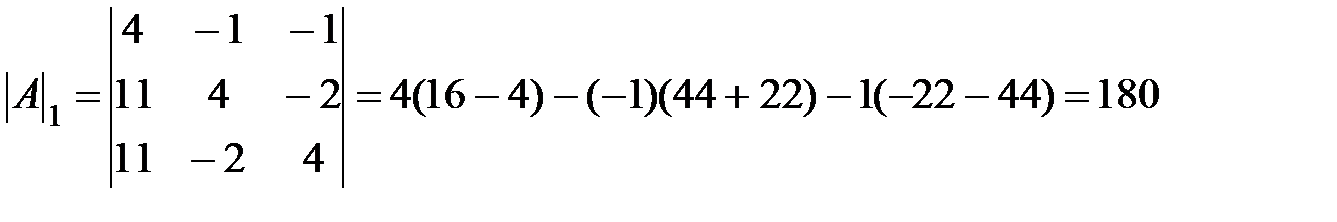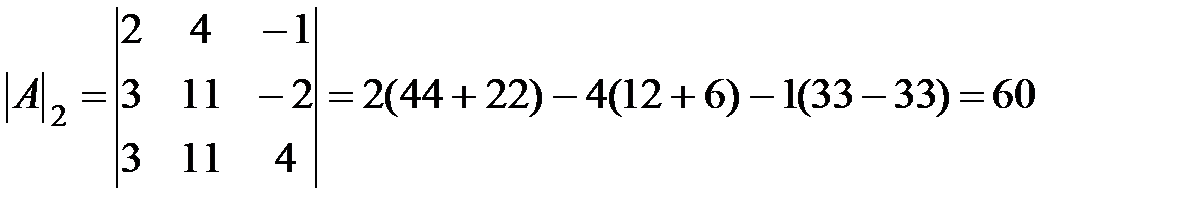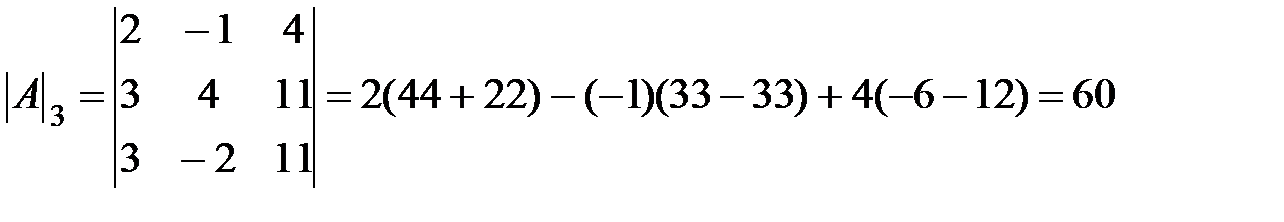По теореме Крамера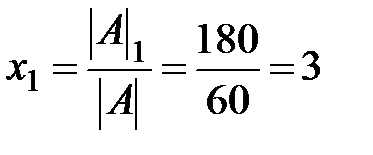 
; 
; 
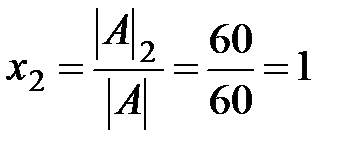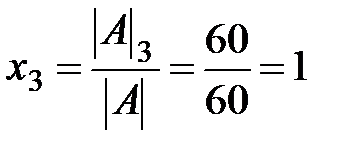. Для проверки результата подставим полученные значения неизвестных в каждое уравнение системы: 
, 
, 
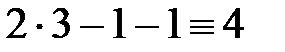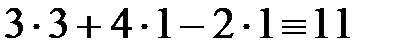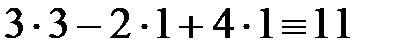. Все уравнения обратились в тождества, значит, решение найдено верно.
Задание 1. По расширенной матрице выписать СЛАУ.
1) 
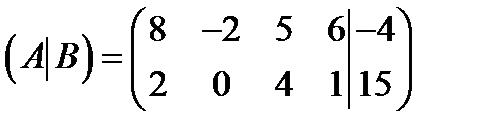
| 2)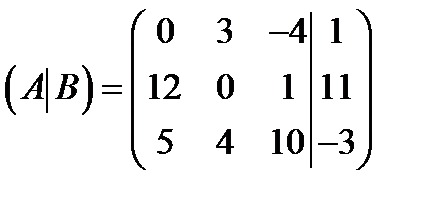 
|
3) 
| 4)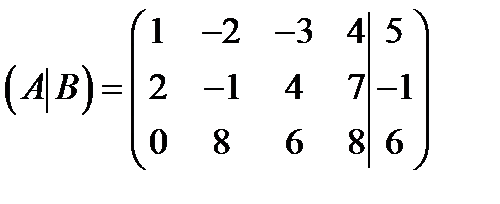 
|
Задание 2. Решить системы уравнений методом Крамера и методом Гаусса.
1) 
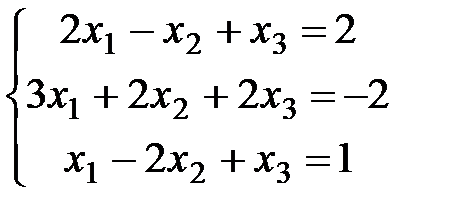
| 2)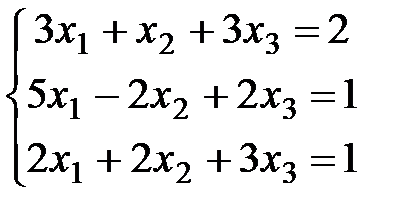 
|
3) 
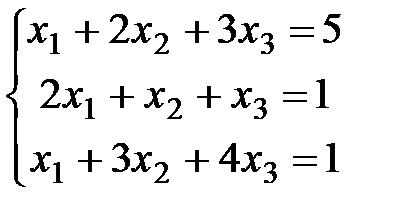
| 4)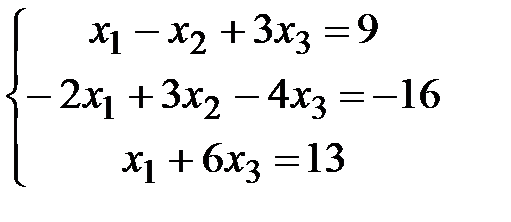 
|
Задание 3. Решить СЛАУ (в случае неопределенной системы выписывать общее и два любых частных решения).
1) 
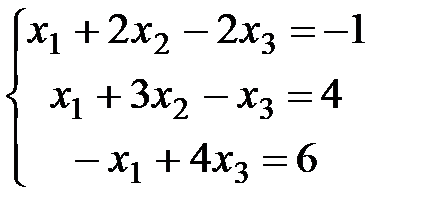
| 2)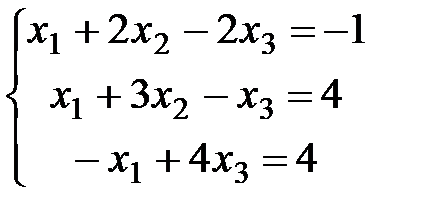 
|
3) 
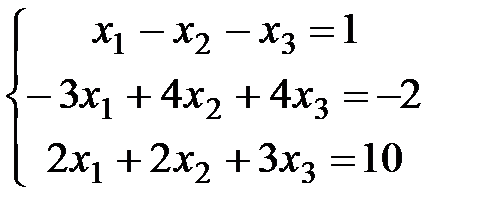
| 4)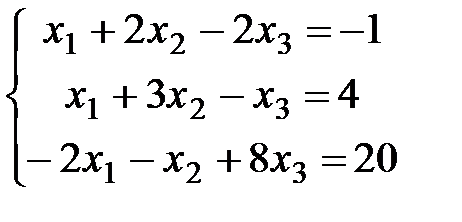 
|
Практическое занятие. Операции над комплексными числами. Приложение комплексных чисел.
Цель.
Решение задач
Пример 1. Решить уравнение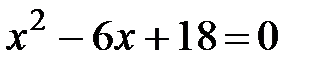 
.
Решение. Дискриминант данного уравнения: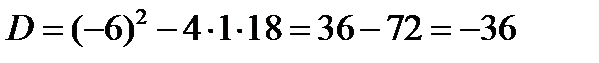 
меньше нуля, но теперь мы можем воспользоваться мнимой единицей:
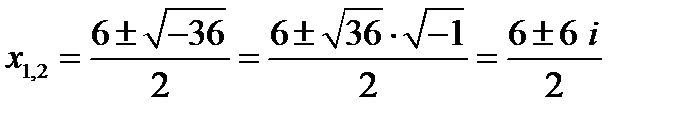, т.е. 
; 
.
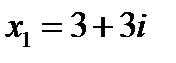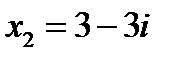Справедливы следующие правила арифметических действий над комплексными числам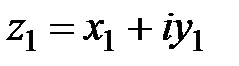и 
и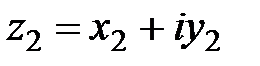 
:
1) 
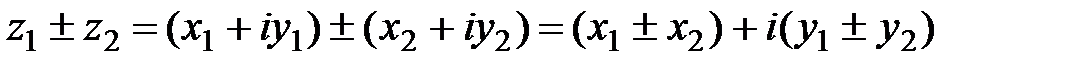(осуществляется сложение или вычитание алгебраических двучленов и приведение подобных);
2) 
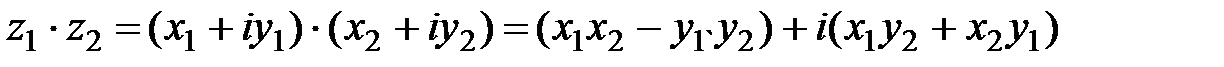(осуществляется перемножение алгебраических двучленов и приведение подобных с учетом того, что 
);
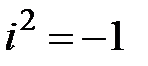3) 
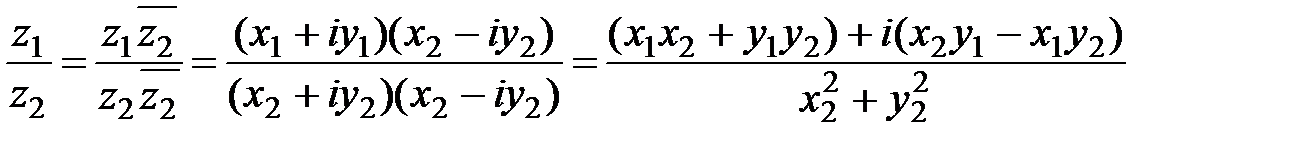(эта операция возможна только в случае, когда 
).
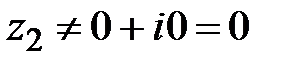Пример 2. Вычислить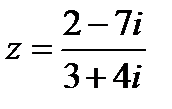 
и указать вещественную и мнимую части полученного комплексного числа.
Решение. Действуя в соответствии с правилами получаем:
;
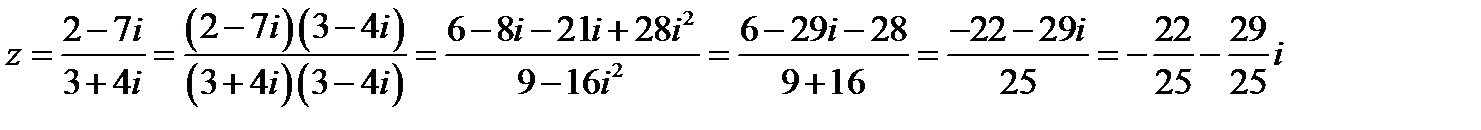поэтому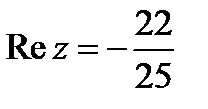 
, 
.
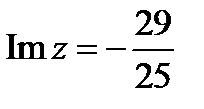Тригонометрическая форма комплексного числа. Каждому комплексному числу вида (1.1) можно поставить в соответствие точку M(x;y) на декартовой плоскости (при этом на оси OX располагаются вещественные числа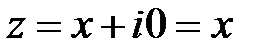 
, а на оси OY – чисто мнимые числа 
).
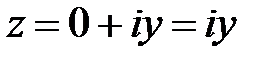Модулем комплексного числа назовем длину отрезка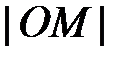 
(или расстояние от начала координат до точки M), т.е. 
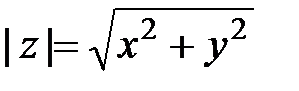. Аргументом комплексного числа ( 
) назовем угол, который вектор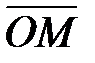 
образует с положительным направлением оси OX. Главное значение аргумента, которое, как правило, используется при осуществлении действий с комплексными числами, удовлетворяет условию 
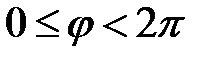. При этом выражение вида
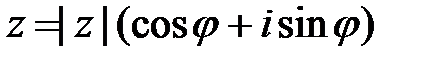(1.2)
называется тригонометрической формой записи комплексного числа.
Преобразуем (1.1)
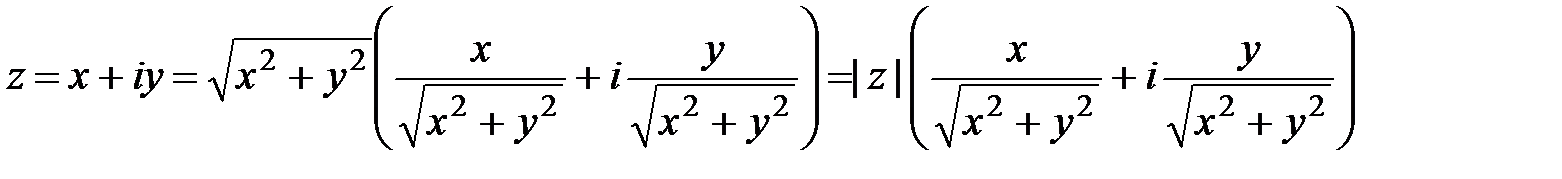
и, сравнивая с (1.2), получаем, что аргумент z можно найти, решив систему
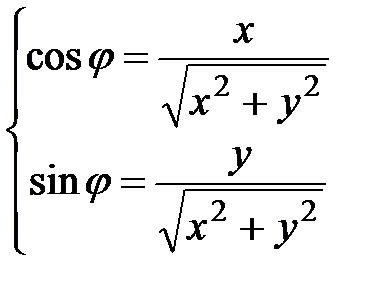или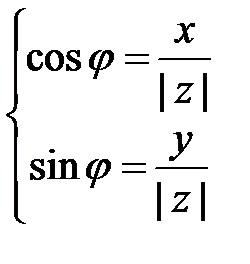 
(1.3.)
Пример 3. Записать комплексное число в тригонометрической форме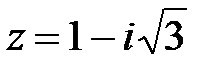 
, указать модуль и аргумент комплексного числа.
Решение. По определению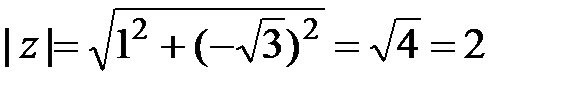 
. Для определения аргумента воспользуемся формулой: 
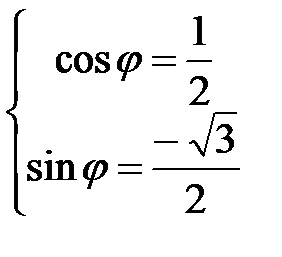. Получаем, что 
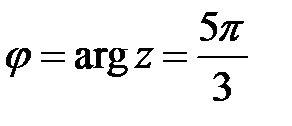. Тригонометрическая форма заданного комплексного числа имеет вид: 
.
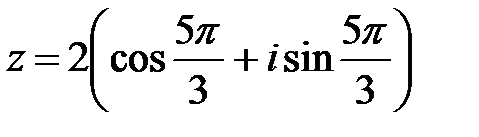Возведение в степень и извлечение корней . Если комплексное число задано тригонометрической формой 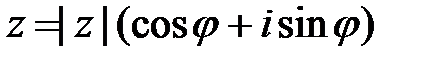, то справедлива формула Муавра
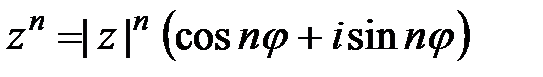. (1.4)
Для извлечения корня n-й степени (n – целое число, большее 1) из комплексного числа, заданного в тригонометрической форме, применяется формула, дающая n значений этого корня:
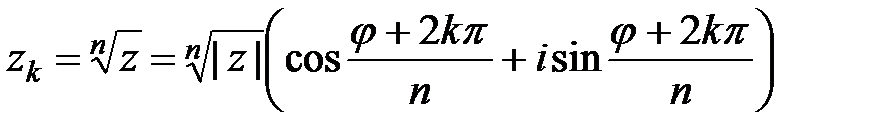, k=0,1,…,n-1. (1.5)
Пример 4. Вычислить: a)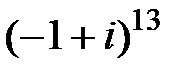 
; b)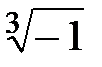 
.
Решение. В задании a), чтобы воспользоваться формулой Муавра, необходимо представить комплексное число в тригонометрической форме. Имеем: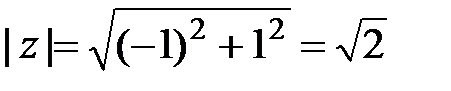 
; 
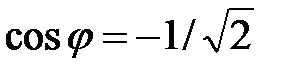и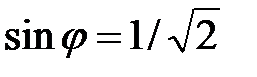 
, т.е. 
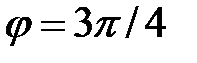(так как соответствующая точка лежит во второй четверти). Следовательно, 
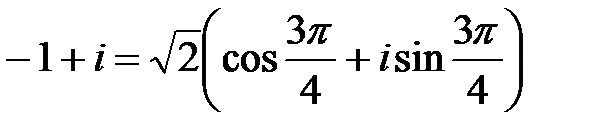и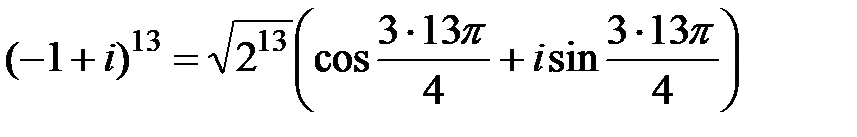 
(в силу (1.4)). Учитывая что 
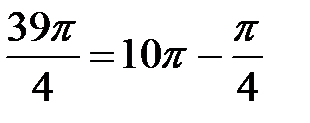и используя свойства тригонометрических функций, получаем:
.
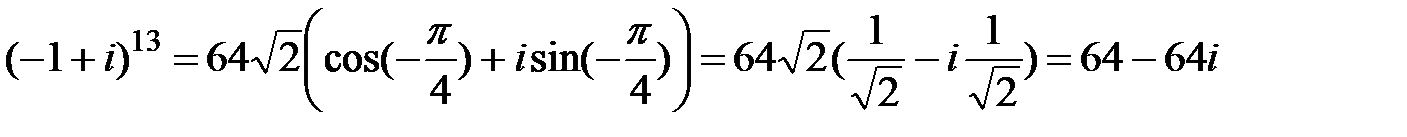В задании b) тригонометрическая форма заданного числа имеет вид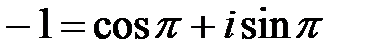 
(|z|=1), поэтому в силу (1.5)
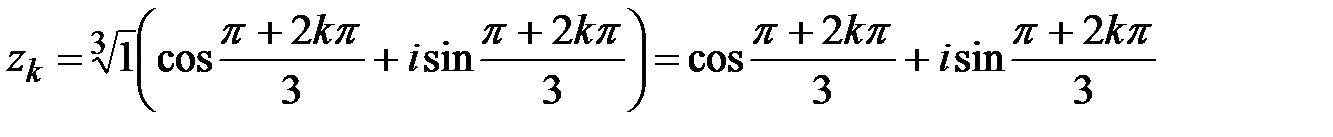, k=0,1,2.
Выписываем три искомых корня:
;
;
.
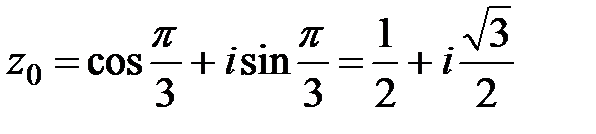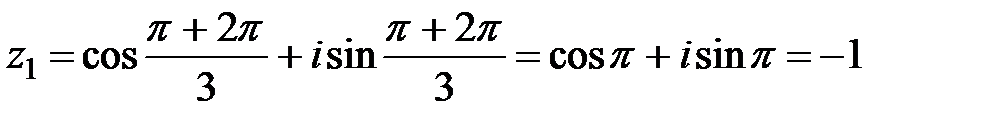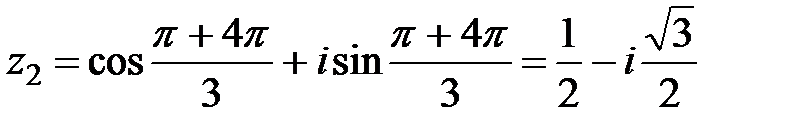Решение прикладных задач
Задача 1
Определить ток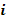 
в неразветвленной части, если токи в ветвях:
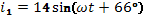
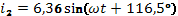
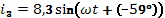
Дано:
, 
, 
, 
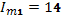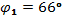
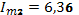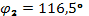
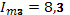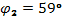
Решение:
Найдем:
1. Комплексные токи в цепях: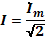 
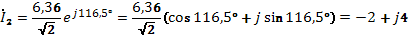(А)
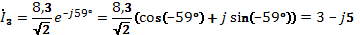(А)
(А)
2. Комплекс тока в неразветвленной части цепи:
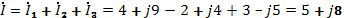
3.Модуль ток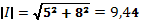а:
(А)
4.Аргумент через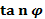 
:
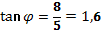, по таблице Брадиса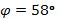 
Ответ: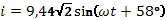 
Задача 2
Известно, что
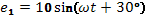
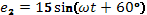
Найти результирующую Э.Д.С.
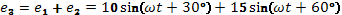
Дано:
, 
, 
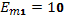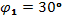
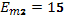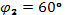
Решение: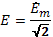 
Найдем:
1. Комплексное Э.Д.С. в цепях:
Найдем:
1. Комплексное Э.Д.С. в цепях:
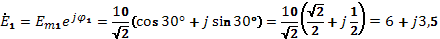
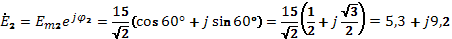
2. Комплекс Э.Д.С. в неразветвленной части цепи:
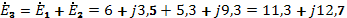
3.Модуль Э.Д.С.:
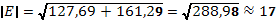
4.Аргумент через :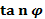
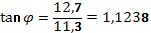, по таблице Брадиса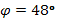 
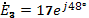
Ответ: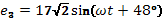 
Практическое занятие. Нахождение вероятности.
Цель. Формировать умения и навыки нахождения вероятности, используя классическую формулу.
Решение задач
Пример 1. Найти вероятность, что при бросании монеты выпадет герб.
Решение. При бросании монеты имеются два равновозможных исхода: “выпадение герба” и “выпадение решки”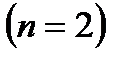 
. Для события 
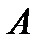– “выпадение герба” благоприятен только один из них 
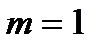. Значит, вероятность 
.
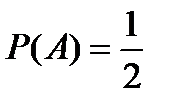Вероятность любого события заключена между нулем и единицей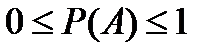 
Можно выделить следующие виды случайных событий:
Событие называется достоверным, если оно обязательно происходит при каждом осуществлении определенной совокупности условий. Вероятность достоверного события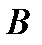 
равна единице: 
.
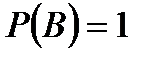Событие называется невозможным, если оно заведомо не произойдет ни при одном осуществлении данной совокупности условий. Вероятность невозможного события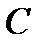 
равна нулю: 
.
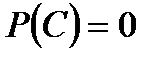Событие называется случайным, если оно может произойти, а может и не произойти при осуществлении данной совокупности условий.
События называются несовместными, если их одновременное появление при осуществлении комплекса условий невозможно, т.е. появление события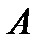 
в данном испытании исключает появление события 
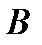в этом же испытании.
События называются единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием.
События называются равновозможными, если есть основания считать, что ни одно из этих событий не является более возможным, чем другие.
Если событие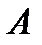 
- какое-либо событие, то событие, состоящее в том, что событие 
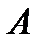не наступило, называется противоположным событию 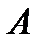и обозначается как 
.
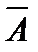События, происходящие при реализации определенного комплекса условий или в результате случайного эксперимента, называются элементарными исходами.
Считается, что при проведении случайного эксперимента реализуется только один из возможных элементарных исходов.
Геометрической вероятностью события A называется отношение площади области g к площади области G, т. е.
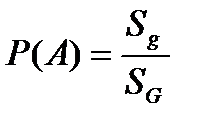
Область g называется благоприятствующей (благоприятной) событию A.
Область, на которую распространяется понятие геометрической вероятности, может быть одномерной (прямая, отрезок) и трехмерной (некоторое тело в пространстве). Обозначая меру (длину, площадь, объем) области через mes, можно записать
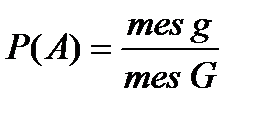
Примеры:
1. В некоторой точке C линии AB длины L произошел разрыв. Какова вероятность того, что точка C удалена от точки A на расстояние не меньше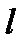 
?
Решение.
Расположим отрезок AB на числовой оси Ox так, как изображено на рис. 2.
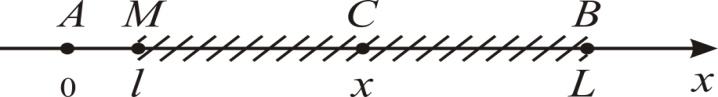
Рис. 2
Пусть x – координата случайной точки C отрезка AB,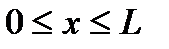 
. Ясно, что исходов опыта (разрыв линии AB в точке C) бесчисленное множество и все они равновозможны. На отрезке AB возьмем точку M, расстояние которой от точки A, равно .
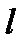Очевидно, что событие A={точка C удалена от точки A на расстояние не меньше 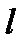} произойдет, если точка C попадет на отрезок MB=[ 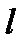,L].
Таким образом, областью, благоприятствующей наступлению события A (на рис. 2 она заштрихована), является отрезок MB, а множеству исходов опыта соответствует отрезок AB=[0,L].
Тогда по формуле (3)
.
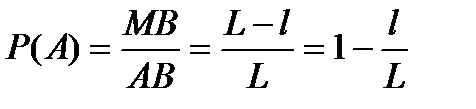2. Сколькими способами можно расставить на полке 5 различных книг?
Решение. Искомое число способов равно числу перестановок из 5 элементов (книг), т. е.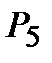 
= 5! = 1·2·3·4·5 = 120.
3. Сколько «слов» по две буквы можно составить из букв a , b , c , d , e , таким образом, чтобы буквы в «словах» не повторялись?
Решение. Т.к. каждое «слово» должно содержать две буквы, то искомое число способов равно числу размещений из 5 элементов (букв) по две, т. е.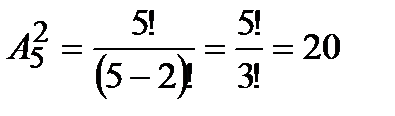 
.
4. Сколькими способами можно выбрать 1 красную гвоздику и 2 розовых из вазы, в которой стоят 10 красных и 4 розовых гвоздики?
Решение. Так как порядок выбора цветов не имеет значения, то красную гвоздику можно выбрать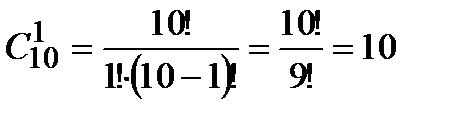 
способами. Выбрать две розовые гвоздики из имеющихся четырех можно 
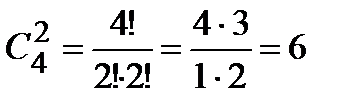способами. Поэтому букет из одной красной и двух розовых гвоздик можно составить, по правилу умножения, 
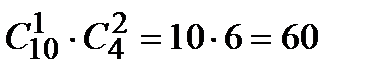способами.
5. Набирая номер телефона, абонент забыл последние 3 цифры, и помня лишь, что эти цифры различны, набрал их наугад. Найти вероятность того, что номер телефона набран правильно.
Решение. Благоприятствующий исход здесь один – правильный набор последних цифр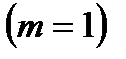 
. Всех возможных исходов здесь будет столько, сколько можно составить комбинаций из 3 цифр, порядок которых имеет значение, значит 
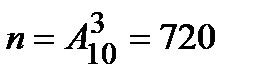. Значит вероятность того, что номер набран правильно (событие 
): 
.
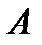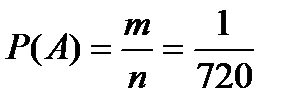6. Среди 100 колес 5 нестандартных. Для контроля выбирается 7 колес. Найти вероятность того, что среди них ровно 3 будет нестандартных.
Решение. Число всевозможных исходов равно количеству комбинаций из 100 колес по 7 штук, т.к. порядок значения не имеет, то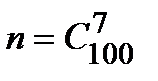 
. Благоприятствующий исход состоит в выборе ровно 3 нестандартных колес из 5 и совместном выборе (7-3) стандартных колес из (100-5), порядок значения не имеет. По правилу произведения 
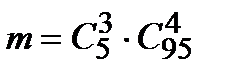. Следовательно, вероятность того, что среди взятых для контроля колес будет ровно 3 нестандартных (событие 
): 
.
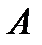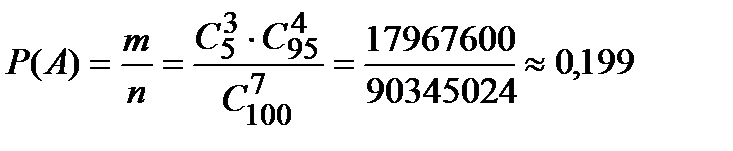Практическое занятие. Нахождение математического ожидания дискретной случайной величины.
Цель. Формировать умения и навыки нахождения математического ожидания дискретной величины.
Решение задач
Наиболее исчерпывающей характеристикой случайной величины является ее закон распределения вероятностей. Однако не всегда обязательно знать весь закон распределения. Иногда можно обойтись одним или несколькими числами, отражающими наиболее важные особенности закона распределения, например, числом, имеющим смысл «среднего значения» случайной величины, или же числом, показывающим средний размер отклонения случайной величины от своего среднего значения. Такого рода числа называются числовыми характеристиками случайной величины. Оперируя числовыми характеристиками, можно решать многие задачи, не пользуясь законом распределения.
Одна из самых важных числовых характеристик случайной величины есть математическое ожидание.
Если известна дискретная случайная величина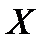 
, закон распределения которой имеет вид
Значения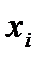 
| 
| 
| … | 
|
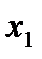
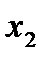
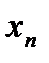
Вероятности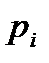 
| 
| 
| … | 
|
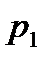
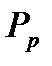
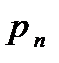
то математическим ожиданием (или средним значением) дискретной величины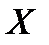 
называется число
.
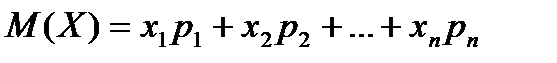Таким образом, математическое ожидание дискретной случайной величины 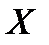равно сумме произведений возможных значений этой величины на их вероятности.
Свойства математического ожидания.
1. Постоянный множитель можно выносить за знак математического ожидания:
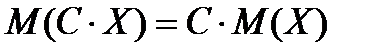
2. Математическое ожидание постоянной величины С равно самой этой величине:
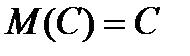
3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
.
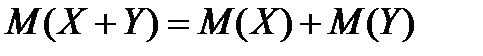4. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий этих величин:
.
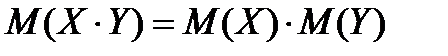Дата: 2019-11-01, просмотров: 234.
