Основной числовой характеристикой степени рассеяния значений случайной величины  относительно ее математического ожидания
относительно ее математического ожидания 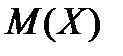 является дисперсия, которая обозначается через
является дисперсия, которая обозначается через 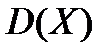 .
.
Определение. Отклонением называется разность между случайной величиной  и ее математическим ожиданием
и ее математическим ожиданием 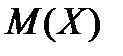 , т.е.
, т.е. 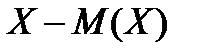 .
.
Отклонение 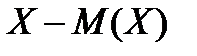 и его квадрат
и его квадрат 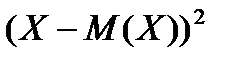 также являются случайными величинами.
также являются случайными величинами.
Определение. Дисперсией дискретной случайной величины  называется математическое ожидание квадрата ее отклонения:
называется математическое ожидание квадрата ее отклонения:
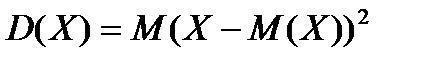 .
.
Свойства дисперсии.
1. Дисперсия постоянной величины С равна 0:
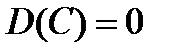 .
.
2. Если  - случайная величина, аС – постоянная, то
- случайная величина, аС – постоянная, то
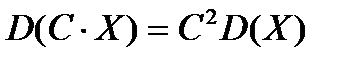
 .
.
3. Если  и
и 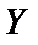 - независимые случайные величины, то
- независимые случайные величины, то
 .
.
4. Для вычисления дисперсий более удобной является формула
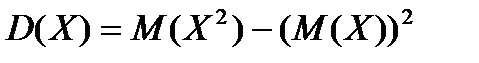 .
.
Пример 3. Дискретная случайная величина распределена по закону:
| -1 | 0 | 1 | 2 |
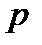
| 0,2 | 0,1 | 0,3 | 0,4 |
Найти  .
.
Решение. Сначала находим 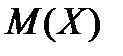 .
.
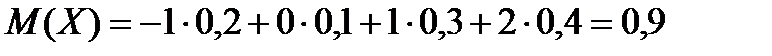 ,
,
а затем 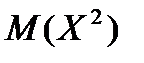 .
.
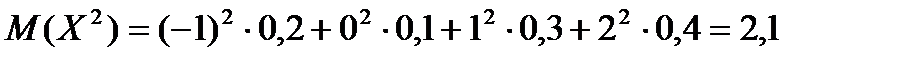 .
.
По формуле 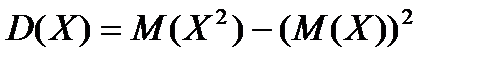 имеем
имеем
 .
.
Средним квадратичным отклонением случайной величины называется корень квадратный из ее дисперсии:
 .
.
Пример 1. 1) Найти математическое ожидание, дисперсию, среднее квадратическое отклонение и 2) функцию распределения дискретной случайной величины Х, заданной законом распределения:
| х | -5 | 2 | 3 | 4 |
| р | 0,4 | 0,3 | 0,1 | 0,2 |
Решение
1) 
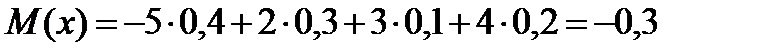
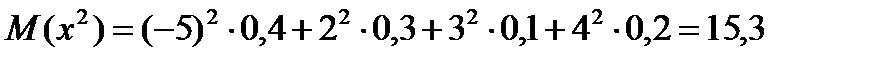
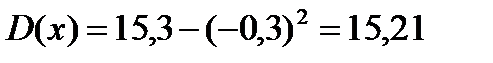
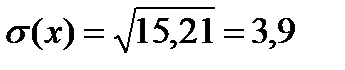
2) Будем задавать различные значения х и находить для них 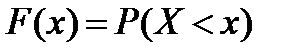
1. Если 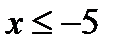 , то F(
, то F(  )=0, F(1)=0;
)=0, F(1)=0;
2. при –5< 
 , F(
, F(  )=P(
)=P(  =-5)=0,4; F(2)=P(
=-5)=0,4; F(2)=P(  <2)=0,4;
<2)=0,4;
3. при 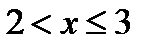 , F(
, F(  )=P(X<
)=P(X<  )=P(
)=P(  =-5)+P(
=-5)+P(  =2)=0,7; F(3)=0,7;
=2)=0,7; F(3)=0,7;
4. при 
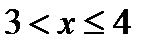 , F(X<
, F(X<  )=P(
)=P(  =-5)+P(
=-5)+P(  =2)+P(
=2)+P(  =3)=0,8; F(4)=0,8;
=3)=0,8; F(4)=0,8;
5. при  >4, F(
>4, F(  )=P(
)=P(  =-5)+P(
=-5)+P(  =2)+P(
=2)+P(  =3)+P(
=3)+P(  =4)=1.
=4)=1.
F(  )=
)= 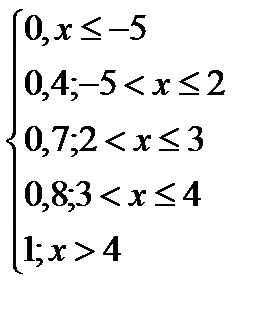

Ответ: -0,3; 15,21; 3,9; F(  ).
).
Практическое занятие. Вычисление пределов
Цель: Формировать умения и навыки вычисления пределов функции
Решение задач
Пример . Найти
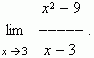
Решение . Подставляя x = 3 в выражение  получим не имеющее смысла выражение
получим не имеющее смысла выражение 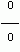 . Поэтому решим по-другому:
. Поэтому решим по-другому:
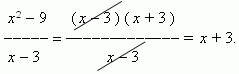
Сокращение дроби в данном случае корректно, так как x  3 , он лишь приближается к 3. Теперь мы имеем:
3 , он лишь приближается к 3. Теперь мы имеем: 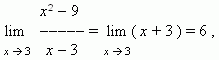
поскольку, если x стремится к 3, то x + 3 стремится к 6 .
Замечательные пределы
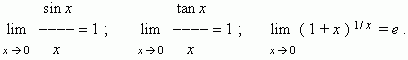
Бесконечно малая и бесконечно большая величины. Если предел некоторой переменной равен 0, то эта переменная называется бесконечно малой.
Пример . Функция y = 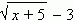 является бесконечно малой при x,
является бесконечно малой при x,
стремящемся к 4, так как 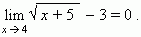
Если абсолютное значение некоторой переменной неограниченно возрастает, то эта переменная называется бесконечно большой.

Бесконечно большая величина не имеет конечного предела, но она имеет так называемый бесконечный предел, что записывается как:
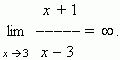
Символ  (бесконечность ) не означает некоторого числа, он означает только, что дробь неограниченно возрастает при x, стремящемся к 3. Следует отметить, что дробь может быть как положительной ( при x > 3 ), так и отрицательной ( при x < 3 ). Если бесконечно большая величина может быть только положительной при любых значениях x, это отражается в записи. Например, при x
(бесконечность ) не означает некоторого числа, он означает только, что дробь неограниченно возрастает при x, стремящемся к 3. Следует отметить, что дробь может быть как положительной ( при x > 3 ), так и отрицательной ( при x < 3 ). Если бесконечно большая величина может быть только положительной при любых значениях x, это отражается в записи. Например, при x 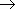 0 функция y = x2 бесконечно большая, но она положительна как при x > 0, так и при x < 0 ; это выражается так:
0 функция y = x2 бесконечно большая, но она положительна как при x > 0, так и при x < 0 ; это выражается так:

Наоборот, функция y = x 2 всегда отрицательна, поэтому
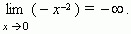
В соответствии с этим, результат в нашем примере можно записать так:
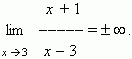

Вычисление пределов (для самостоятельного выполнения заданий)
1.Найдите пределы последовательностей:
1) 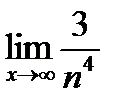 ; 3)
; 3)  ;
;
2) 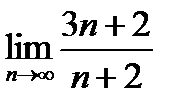 ; 4)
; 4) 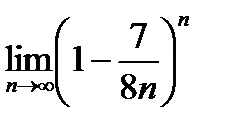 .
.
2.Найдите пределы функций:
1)  ;
;
2) 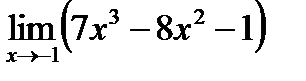 ;
;
3) 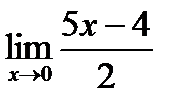 ;
;
4) 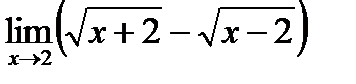 ;
;
5)  .
.
3. Раскрытие неопределенностей вида 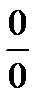 . Найдите пределы:
. Найдите пределы:
1) 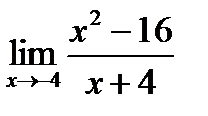 ; 3)
; 3) 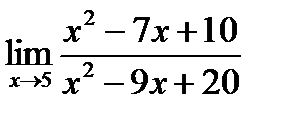 ;
;
2) 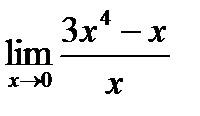 ; 4)
; 4) 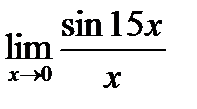 .
.
4. Раскрытие неопределенностей вида 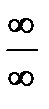 . Найдите пределы:
. Найдите пределы:
1)  ; 2)
; 2) 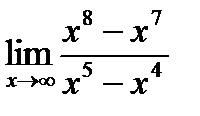 .
.
Практическое занятие. Исследование функций на непрерывность.
Цель: Формировать умения и навыки исследования функций на непрерывность
Решение задач
Пример 1 Пусть 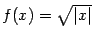 и
и 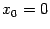 . Тогда
. Тогда  и
и  . Эти значения совпадают, значит, функция
. Эти значения совпадают, значит, функция 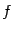 непрерывна в точке
непрерывна в точке 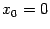 .
.
(Функция 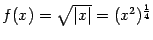 ‒ элементарная функция;
‒ элементарная функция; 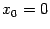 ‒ точка её области определения
‒ точка её области определения 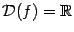 . Все элементарные функции непрерывны во всех внутренних точках своих областей определения, в том числе и эта. Так что в этом примере можно было бы заменить
. Все элементарные функции непрерывны во всех внутренних точках своих областей определения, в том числе и эта. Так что в этом примере можно было бы заменить 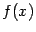 любой элементарной функцией, а
любой элементарной функцией, а 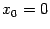 -- любой внутренней точкой области
-- любой внутренней точкой области 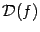 , и вывод остался бы тем же.)
, и вывод остался бы тем же.)
Пример 2 Рассмотрим функцию 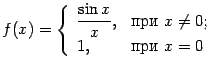 и точку
и точку 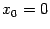 . При
. При 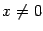 функция задаётся формулой
функция задаётся формулой 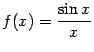 , при этом имеем
, при этом имеем 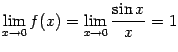 (первый замечательный предел). Это значение совпадает с тем, которое задано при
(первый замечательный предел). Это значение совпадает с тем, которое задано при 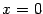 :
: 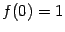 . Итак,
. Итак, 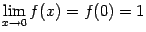 , что означает непрервыность функции
, что означает непрервыность функции 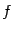 при
при 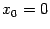 .
.
Тем, кто внимательно изучил данное в главе 2 общее понятие базы предела, можно предложить продумать и доказать следующее утверждение:
Определение точек разрыва
Дадим теперь определение точек разрыва функции.
Определение Точка  называется точкой разрыва функции
называется точкой разрыва функции 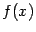 , если она определена в некоторой проколотой окрестности точки
, если она определена в некоторой проколотой окрестности точки  (то есть, определена на некотором интервале, для которого
(то есть, определена на некотором интервале, для которого  служит внутренней точкой, но в самой точке
служит внутренней точкой, но в самой точке  , возможно, не определена) и выполняется, хотя бы одно из следующих условий:
, возможно, не определена) и выполняется, хотя бы одно из следующих условий:
1) не существует предела слева 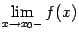 ;
;
2) не существует предела справа  ;
;
3) пределы слева 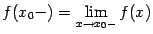 и справа
и справа 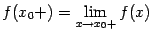 существуют, но не равны друг другу:
существуют, но не равны друг другу: 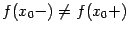 ;
;
4) пределы слева 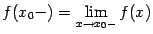 и справа
и справа 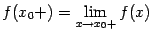 существуют и равны друг другу:
существуют и равны друг другу: 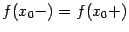 , но не совпадают со значением функции в точке
, но не совпадают со значением функции в точке  :
: 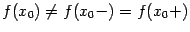 , или функция
, или функция 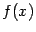 не определена в точке
не определена в точке  .
.
Если имеет место либо случай 3, либо случай 4, то точка разрыва  называется точкой разрыва первого рода, а поведение функции в окрестности точки
называется точкой разрыва первого рода, а поведение функции в окрестности точки  называется разрывом первого рода в точке
называется разрывом первого рода в точке  ; в случае 4 точка разрыва первого рода называется устранимой точкой разрыва, а разрыв функции в этой точке -- устранимым разрывом.
; в случае 4 точка разрыва первого рода называется устранимой точкой разрыва, а разрыв функции в этой точке -- устранимым разрывом.
Если же имеет место либо случай 1, либо случай 2 (либо и тот и другой сразу), то точка разрыва  называется точкой разрыва второго рода, а поведение функции в окрестности этой точки ‒ разрывом второго рода в точке
называется точкой разрыва второго рода, а поведение функции в окрестности этой точки ‒ разрывом второго рода в точке  .
.
Итак, если функция 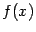 имеет разрыв первого рода в точке
имеет разрыв первого рода в точке  , то существуют, как часто говорят, значения функции "на берегах разрыва":
, то существуют, как часто говорят, значения функции "на берегах разрыва": 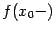 и
и 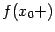 , но точка
, но точка  не является точкой непрерывности.
не является точкой непрерывности.

.  -- точка разрыва первого рода
-- точка разрыва первого рода
Если значения на берегах разрыва разные, то значение функции в точке  может быть любым (или вообще отсутствовать), всё равно
может быть любым (или вообще отсутствовать), всё равно  будет давать разрыв первого рода. Если же значения на берегах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке
будет давать разрыв первого рода. Если же значения на берегах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке  , либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию
, либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию 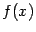 в точке
в точке  , положив
, положив 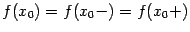 , то полученная изменённая функция будет уже непрерывна в точке
, то полученная изменённая функция будет уже непрерывна в точке  и разрыв в точке
и разрыв в точке  исчезнет; отсюда и название такого разрыва ‒ устранимый.
исчезнет; отсюда и название такого разрыва ‒ устранимый.
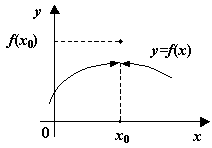
.  -- точка устранимого разрыва
-- точка устранимого разрыва
Наконец, к разрывам второго рода, как видно из определения, относятся все разрывы, которые не принадлежат к разрывам первого рода; некоторые из возможных способов поведения функции в окрестности точки  , где происходит разрыв второго рода, представлены на следующем рисунке.
, где происходит разрыв второго рода, представлены на следующем рисунке.
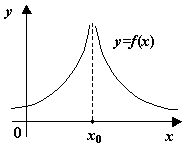
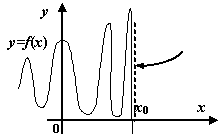
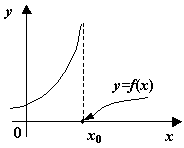
.  -- точка разрыва второго рода. Некоторые возможные варианты
-- точка разрыва второго рода. Некоторые возможные варианты
Пример 3 Рассмотрим функцию 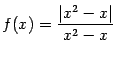 , для которой
, для которой
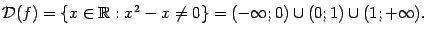
Функция имеет разрывы при 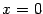 и при
и при 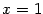 . Нетрудно видеть, что при
. Нетрудно видеть, что при 
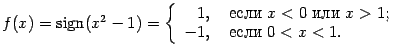 В точках
В точках 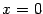 и
и 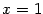 функция имеет неустранимые разрывы первого рода. В точке
функция имеет неустранимые разрывы первого рода. В точке 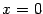 имеем:
имеем:
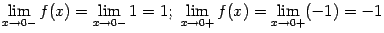
(значения на краях разыва существуют, но не совпадают); в точке 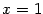 ‒
‒
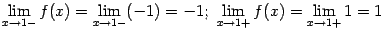
(снова пределы слева и справа существуют, но не совпадают).
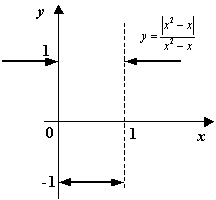
График функции 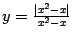
Пример 4 Функция  имеет при
имеет при 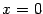 разрыв второго рода, так как
разрыв второго рода, так как 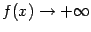 при
при 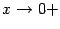 и
и 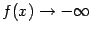 при
при 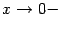 .
.
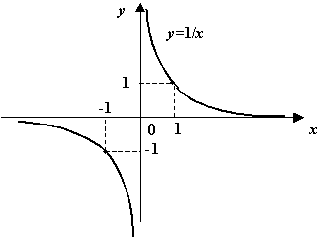
Рис.3.6.График функции 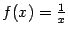
Пример 5 Функция 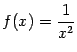 имеет при
имеет при 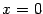 разрыв второго рода, так как
разрыв второго рода, так как 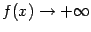 при
при 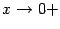 и при
и при 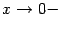 .
.
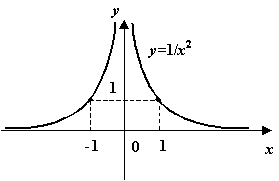
Рис. График функции 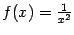
Первый замечательный предел равен 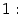
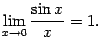
Вторым замечательным пределом называется предел

Число 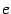 , заданное этим пределом, играет очень большую роль, как в математическом анализе, так и в других разделах математики. Число
, заданное этим пределом, играет очень большую роль, как в математическом анализе, так и в других разделах математики. Число 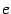 часто называют основанием натуральных логарифмов.
часто называют основанием натуральных логарифмов.
Второй замечательный предел существует. Его значение 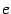 ‒ число, лежащее между 2 и
‒ число, лежащее между 2 и 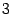 .
.
Более подробное изучение числа 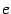 показывает, что
показывает, что 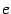 ‒ иррациональное число, несколько первых десятичных знаков которого таковы:
‒ иррациональное число, несколько первых десятичных знаков которого таковы:
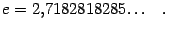
Пример 6. Найдём предел  .
.
Здесь основание степени имеет предел
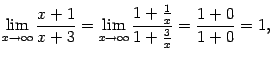
а показатель степени  . Поэтому можно применять тот же приём сведения ко второму замечательному пределу, что в предыдущем примере. Для начала найдём, что следует взять за бесконечно малую величину
. Поэтому можно применять тот же приём сведения ко второму замечательному пределу, что в предыдущем примере. Для начала найдём, что следует взять за бесконечно малую величину  . Поскольку основание степени стремится к 1, то оно равно
. Поскольку основание степени стремится к 1, то оно равно 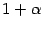 , где
, где 
Значит,
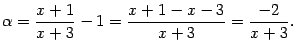
Теперь преобразуем функцию, стоящую под знаком предела:
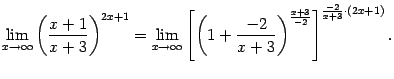
Выражение, стоящее в квадратных скобках, имеет вид  и при
и при  стремится к числу
стремится к числу 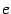 (это второй замечательный предел), а предел показателя степени мы найдём отдельно:
(это второй замечательный предел), а предел показателя степени мы найдём отдельно:

Поэтому
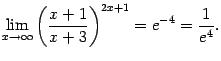
(
Практическое занятие. Нахождение производной функции.
Цель: Приобрести навыки вычисления производной функции.
Справочный материал и примеры
Производной функции 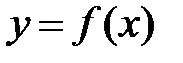 называется конечный предел отношения приращения функции
называется конечный предел отношения приращения функции 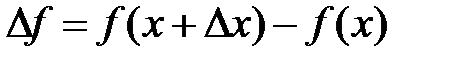 к приращению независимой переменной
к приращению независимой переменной 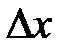 при стремлении последнего к нулю:
при стремлении последнего к нулю:
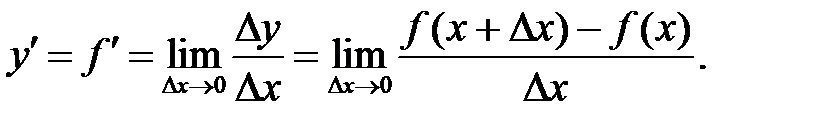 (1)
(1)
Обозначения производной в точке х0:
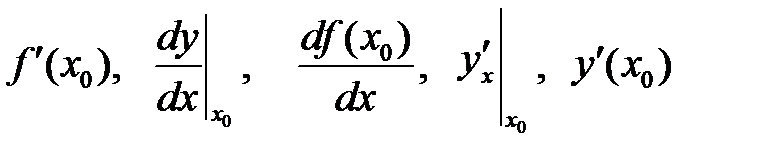 и другие.
и другие.
Если функция в точке х0 (или на промежутке Х) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке Х).
Процесс отыскания производной называется дифференцированием.



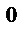
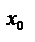
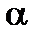

N
Геометрический смысл производной. 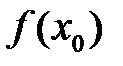
Если кривая задана уравнением 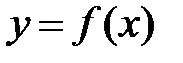 ,
,
то  — угловой коэффициент касательной к графику функции в этой точке (
— угловой коэффициент касательной к графику функции в этой точке (  ).
).
Уравнение касательной к кривой 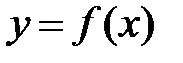
в точке х0 (прямая М0Т) имеет вид:
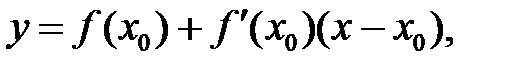 (2)
(2)
а уравнение нормали (М0N):
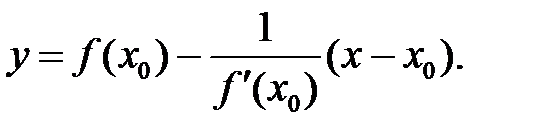 (3)
(3)
Правила дифференцирования
| № пп | U = u(x), V=V(x) — дифференцируемые функции | № п/п | U = u(x), V=V(x) – дифференцируемые функции |
| I | 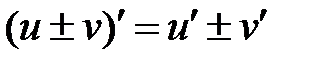
| VI | Производная сложной функции 
|
| II | 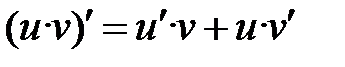
|
VII
Функция задана параметрическими уравнениями 
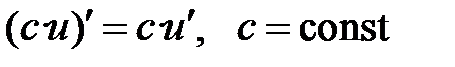
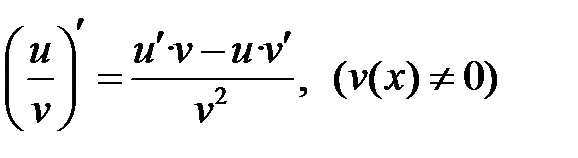
VIII
Если 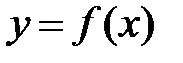 и
и  —
—
взаимно обратные функции,
то 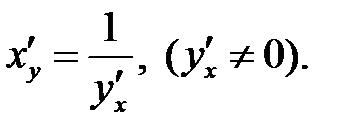

Формулы дифференцирования
| № | Производная элементарной функции |
| 1 | 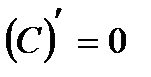
|
| Степенная функция | |
| 2 | 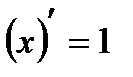
|
| 3 | 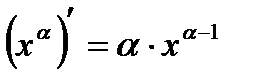
|
| 4 | 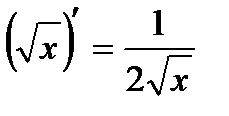
|
| 5 | 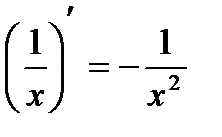
|
| Показательная функция | |
| 6 | 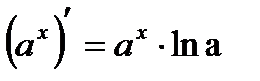
|
| 7 | 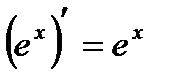
|
| Логарифмическая функция | |
| 8 | 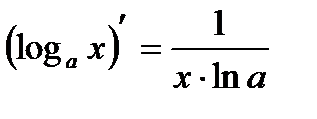
|
| 9 | 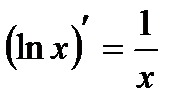
|
| 10 | 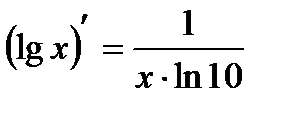
|
| Тригонометрическая функция | |
| 11 | 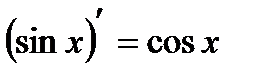
|
| 12 | 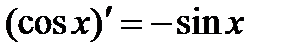
|
| 13 | 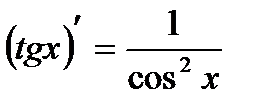
|
| 14 | 
|
| Обратная тригонометрическая функция | |
| 15 | 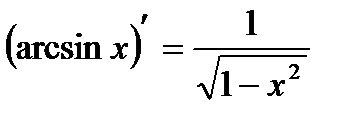
|
| 16 | 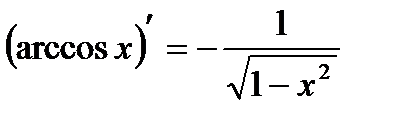
|
| 17 | 
|
| 18 | 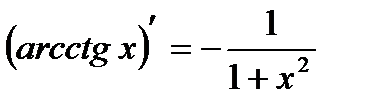
|
Пример 1. Найти производные функций:
а)  б)
б)  в)
в)  г)
г) 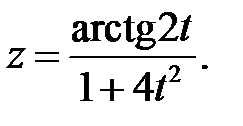
Решение.
а) Используя правила I, III и формулу (3), получим:
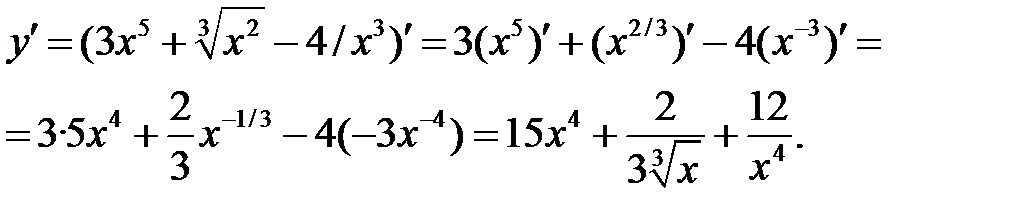
б) Используя правила дифференцирования произведения функций II, разности I, формулы (5), (7), (8) и учитывая, что независимая переменная есть t, т. е. t=1, получим:
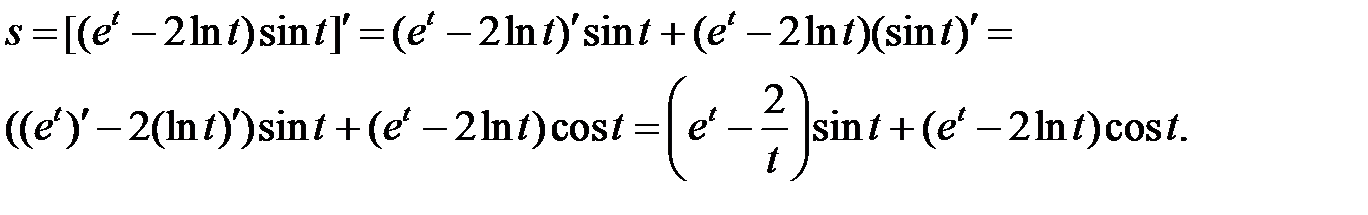
в) Используя правила дифференцирования частного IV, суммы I, III
и формулы (3), (14), учитывая, что t=1, получим:
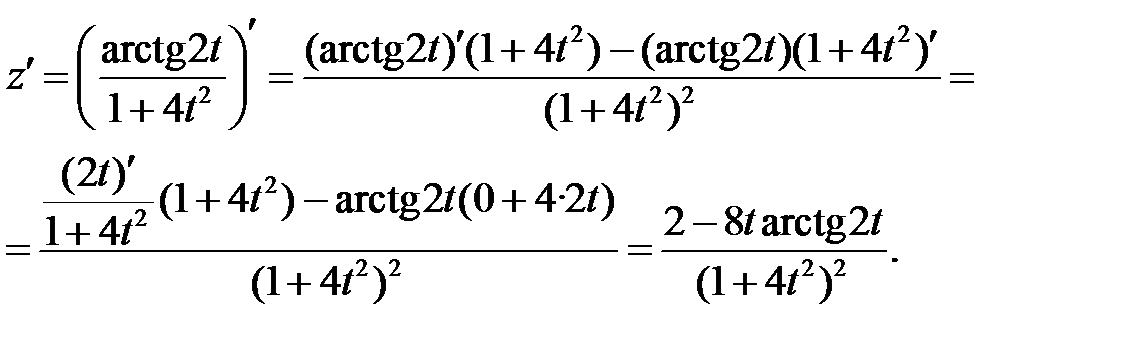
Пример 2. Составить уравнение касательной и нормали к кривой 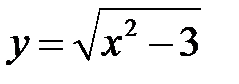 в точке с абсциссой х0=2.
в точке с абсциссой х0=2.
Используем уравнения касательной (2) и нормали (3):
1) 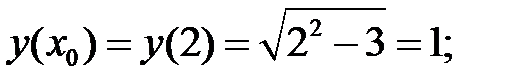
2) 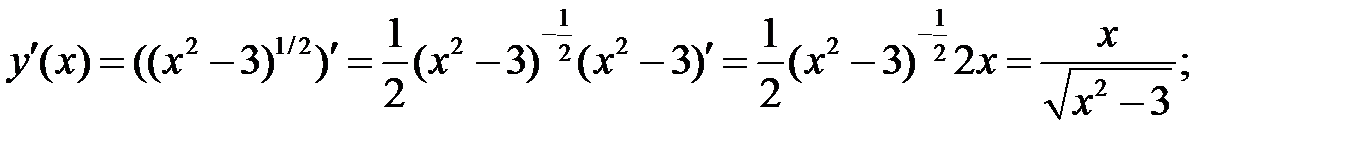
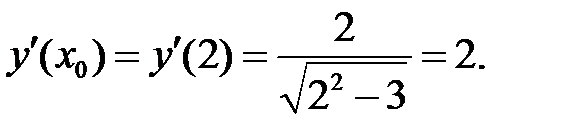
Подставим 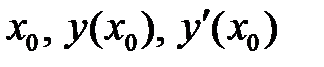 в уравнения и получим:
в уравнения и получим: 
или 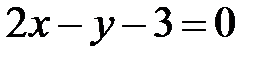 — уравнение касательной.
— уравнение касательной.
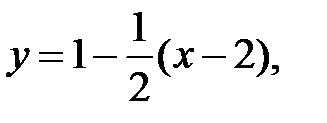 или
или 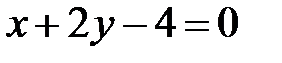 — уравнение нормали.
— уравнение нормали.
Пример 3 . Найти производную  , если функция задана параметрически:
, если функция задана параметрически: 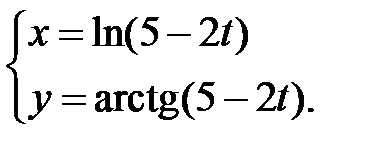
Используем правило VII 
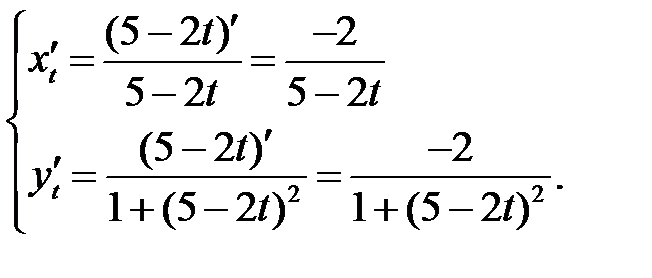

Пример 4. Найти дифференциалы функций:
а)  б)
б)  в)
в) 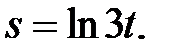
Для дифференциала функции 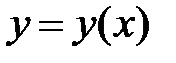 справедлива формула
справедлива формула 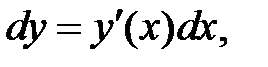 т. е. дифференциал функции равен произведению производной от функции на дифференциал независимой переменной.
т. е. дифференциал функции равен произведению производной от функции на дифференциал независимой переменной.
Решение.
а) 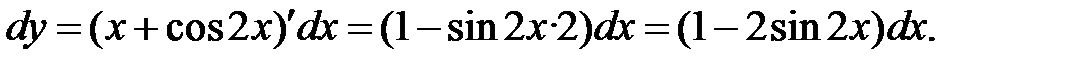
б) 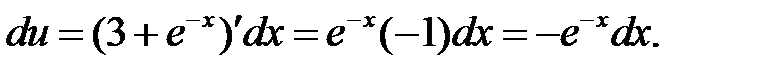
в) 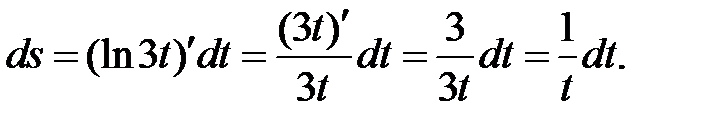
Пример 5. Найти производную функции  логарифмическим дифференцированием
логарифмическим дифференцированием
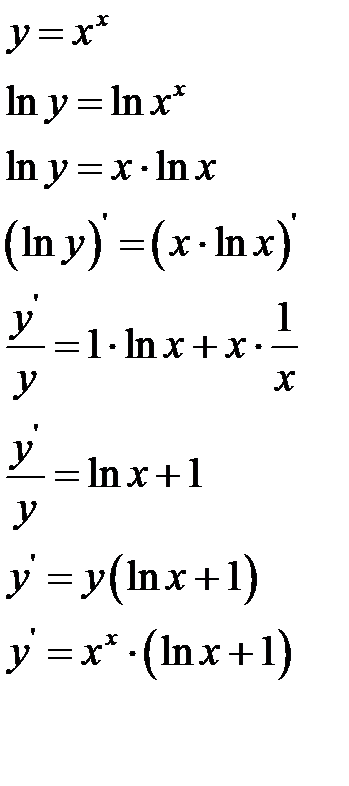
Правило Лопиталя. Предел отношения двух б.м. 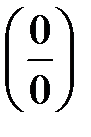 или б.б.
или б.б. 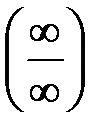 функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:
функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:
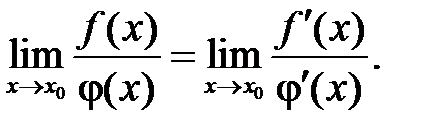 (5)
(5)
Чтобы использовать правило Лопиталя для раскрытия неопределённостей других типов, выражение под знаком предела следует преобразовать элементарными способами так, чтобы получить неопределенность 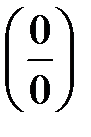 или
или 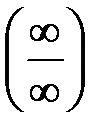 и затем использовать формулу (5).
и затем использовать формулу (5).
Пример 6. Найти пределы, используя правило Лопиталя или элементарные способы раскрытия неопределённостей:
а) 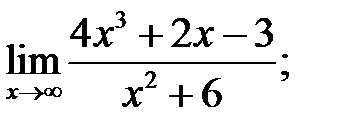 б)
б) 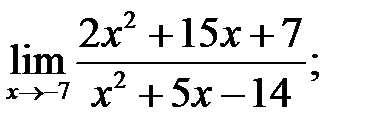
Решение.
а) Подставляя в функцию вместо х предельное значение  , определим предел числителя и знаменателя.
, определим предел числителя и знаменателя.
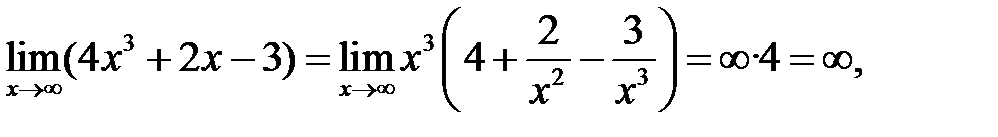 т. к.
т. к. 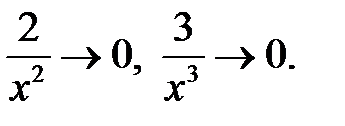
Аналогично: 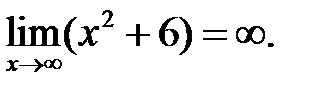
Имеем неопределенность вида 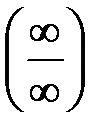 . Используем правило Лопиталя:
. Используем правило Лопиталя:

б) 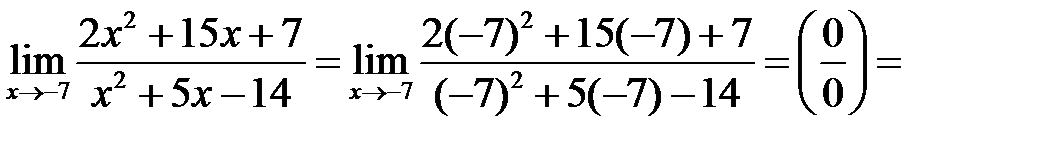
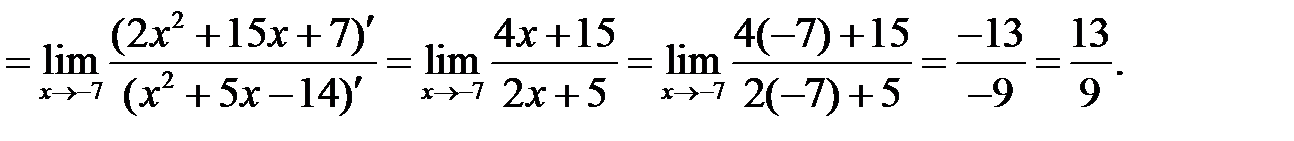
Задания для практической работы
Задание 1. Найти производные 1-го порядка данных функций
1) 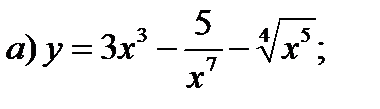
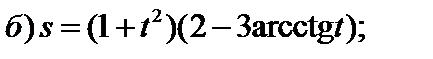
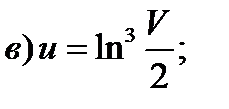

2) 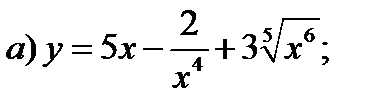
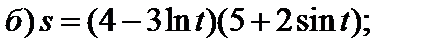
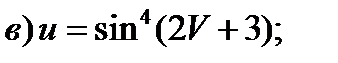
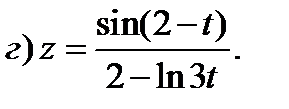
3) 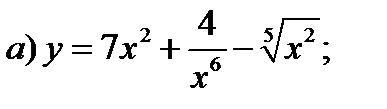
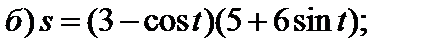
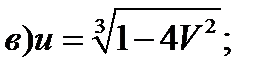
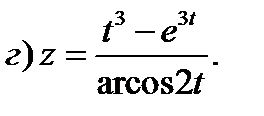
4) 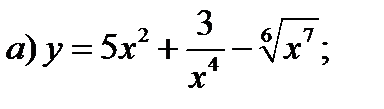
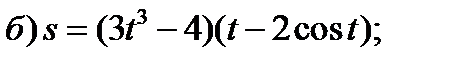
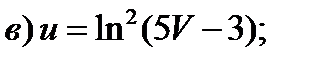
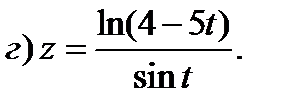
5) 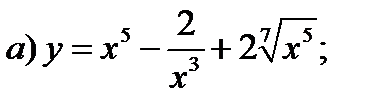
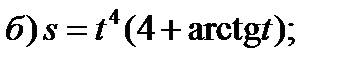
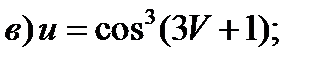
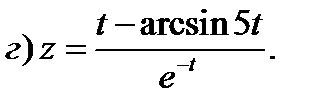
6) 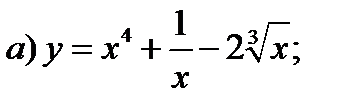
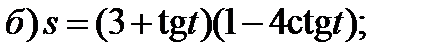
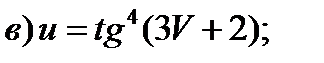

Задание 2. Составить уравнение касательной и нормали к кривой y=f(x) в точке с абсциссой х0.
1) 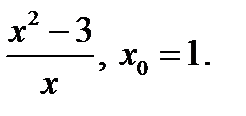
2) 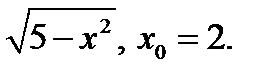
3) 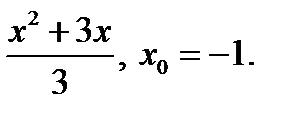
4) 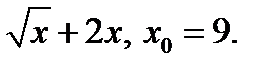
5) 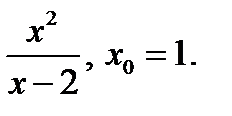
6) 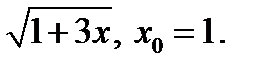
Задание 3. Найти производную 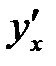 функции y=у(x), заданной параметрически:
функции y=у(x), заданной параметрически: 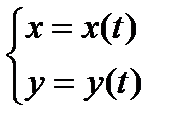
1) 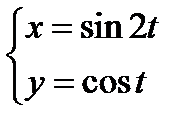
2) 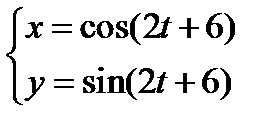
3) 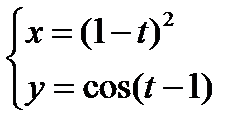
4) 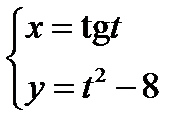
5) 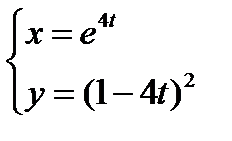
6) 
Задание 4. Найти дифференциалы функций:
1) 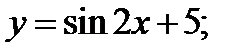
2) 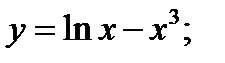
3) 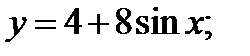
4) 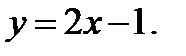
5) 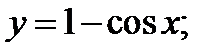
6) 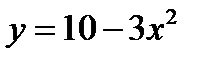
Задание 5. Найти производную функции логарифмическим дифференцированием
1) 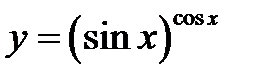
2) 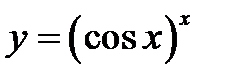
3) 
4) 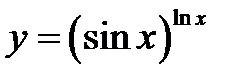
5) 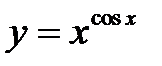
Задание 6 . Найти пределы, используя правило Лопиталя.
1) 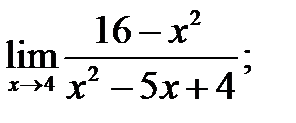
2) 
3) 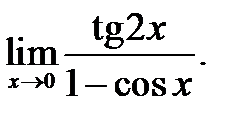
4) 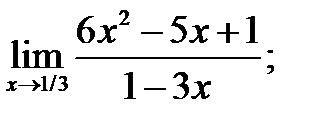
5) 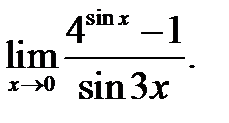
Практическое занятие. Нахождение неопределённого интеграла
Дата: 2019-11-01, просмотров: 319.