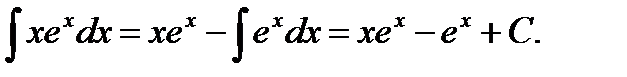
При вычислении интеграла с помощью интегрирования по частям важно правильно выбрать функции 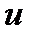и .

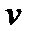Пример 2. Найти интеграл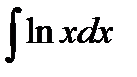

Решение.

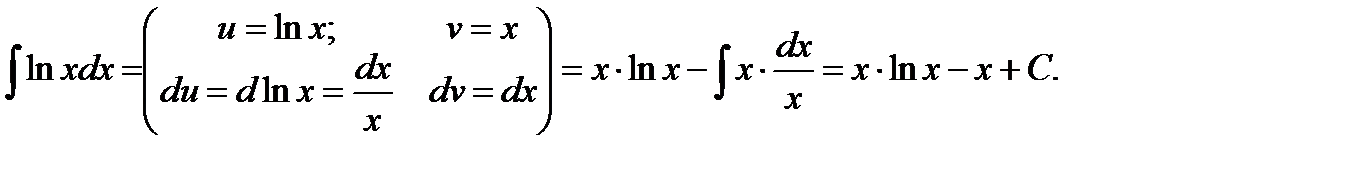
Пример 3. Найти интеграл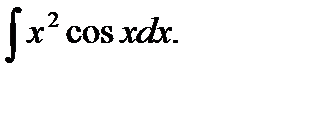

Решение.

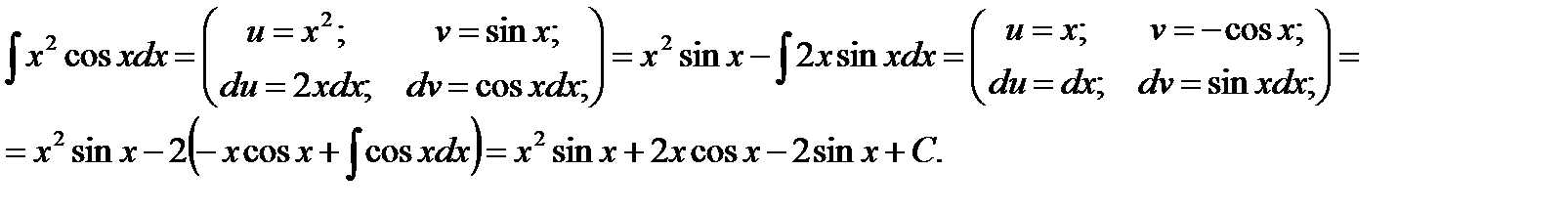
Тема 7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Связь между определенным и неопределенным интегралом осуществляется с помощью основной формулы интегрального исчисления - формулы Ньютона-Лейбница.

Основная теорема интегрального исчисления

Пусть функция у= f (х) непрерывна на отрезке [а, b] и F ( x ) - любая первообразная для f(x) на [а, b]. Тогда определенный интеграл от функции f(х) на [а, b] равен приращению первообразной F ( x ) на этом отрезке, т.е.

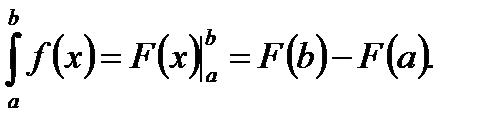                                    (6.1)

Вычисление объемов тел вращения

Пусть на отрезке [а, b] задана непрерывная функция у= f (х).

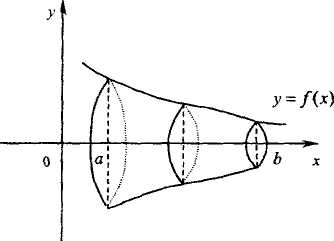
Объем V_x тела, полученного вращением вокруг оси абсцисс криволинейной трапеции, ограниченной линиями y = f ( x ), y =0, x = a , x = b , вычисляется по формуле

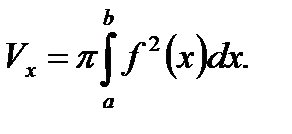                                                        (6.2)

Объем V_y тела, полученного вращением вокруг оси ординат криволинейной трапеции, ограниченной линиями 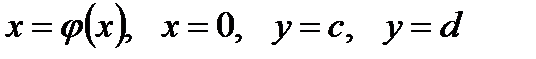, вычисляется по формуле

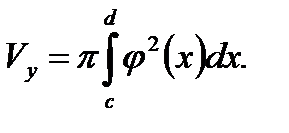                                                         (6.3)

Задание

а) Вычислить объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линиями: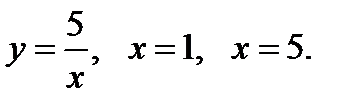

Решение

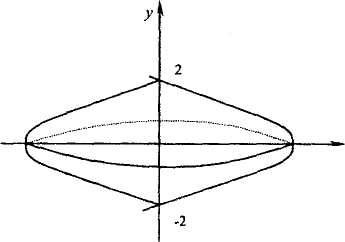
Изобразим на чертеже фигуру, объем которой требуется найти.

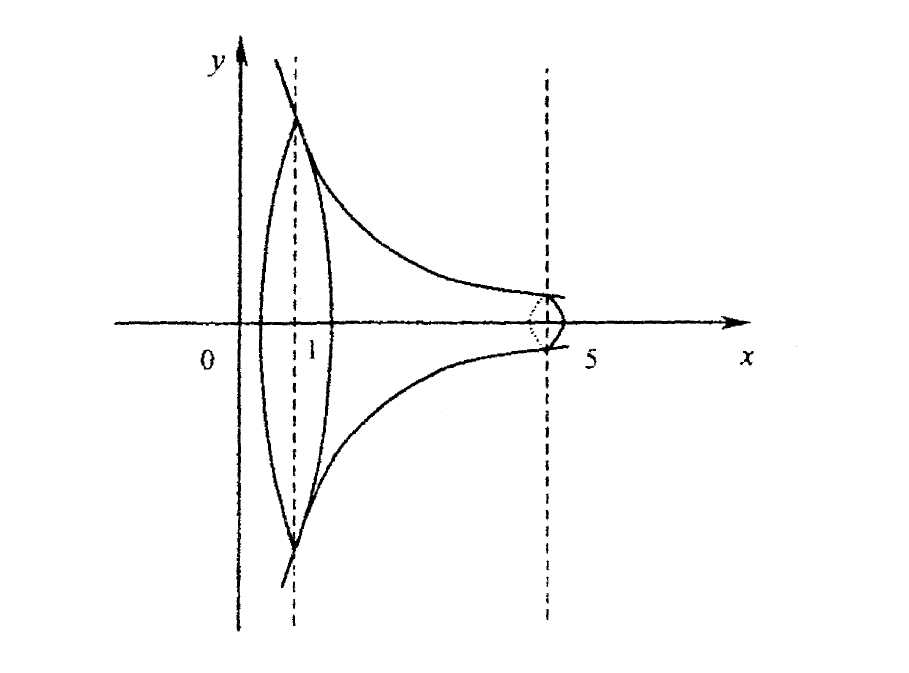
Так как полученная фигура вращается вокруг оси Ох, то воспользуемся формулой (6.2)

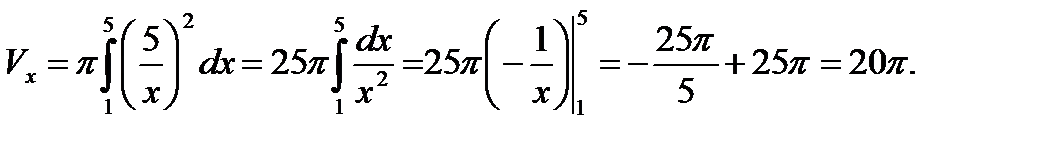
(см. (6.1)).

б) Вычислить объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной линиями: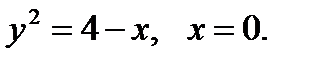

Решение

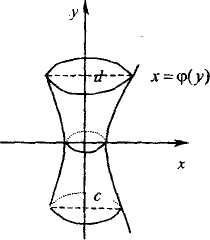
Изобразим на чертеже фигуру, объем которой требуется найти.

 Так как полученная фигура вращается вокруг оси Оу, то запишем уравнение линии у²=4-х в виде х = 4-у² и воспользуемся формулой (6.3).

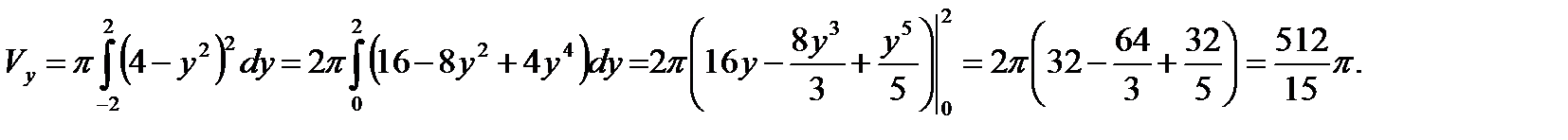
Тема 8. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Уравнение вида

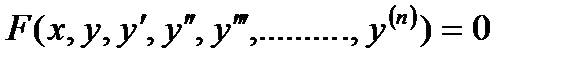,                            (7.1)

связывающее независимую переменную х, искомую функцию 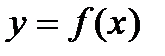 и ее производные различных порядков, называется обыкновенным дифференциальным уравнением.

       Порядок п старшей производной, входящей в запись уравнения называется порядком дифференциального уравнения.

Уравнение, содержащее производные или дифференциалы не выше первого порядка, называется дифференциальным уравнением первого порядка.

Решением дифференциального уравнения (7.1) называется функция 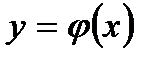, которая, будучи подставлена в уравнение (7.1), обращает его в тождество.

Процесс нахождения решения некоторого дифференциального уравнения называется интегрированием данного дифференциального уравнения.

Общим решением дифференциального уравнения (7.1) п-ого порядка называется такое его решение

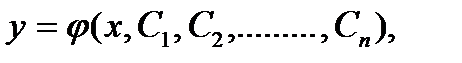
которое является функцией переменной х и п произвольных независимых постоянных . (Независимость постоянных означает отсутствие каких-либо соотношений между ними).

       Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных .