1) длину стороны АВ;

2) тангенс внутреннего угла А;

3) уравнение высоты, проведенной через вершину С;

4) уравнение медианы, проведенной через вершину С;

5) точку пересечения высот треугольника;

6) длину высоты, опущенной из вершины С;

7) систему линейных неравенств, определяющих треугольник ABC.

Сделать чертеж.

y

Решение

1. Длину стороны АВ найдем по формуле (1.1), расстояния между двумя точками A(-2;3) и B(4; 1):

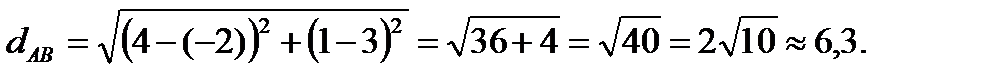
2. Внутренний угол А треугольника ABC можно найти по формуле (1.9). Но нам неизвестны угловые коэффициенты прямых АС и АВ. Найдем уравнения данных прямых, воспользовавшись уравнением прямой, проходящей через две данные точки. По формуле (1.6)

      AC :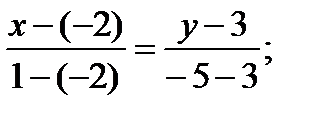

                  ;

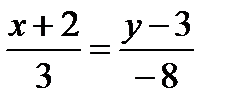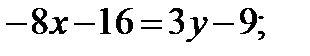
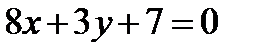                          или

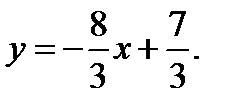
     AB: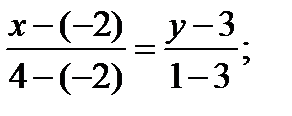

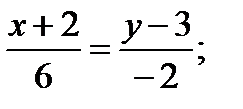
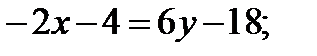
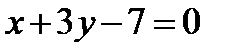                         или

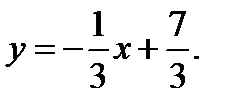
Из уравнений данных прямых следует, что их угловые коэффициенты

                                     ,

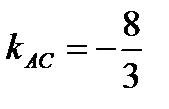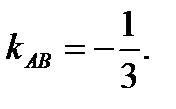
Теперь по формуле (1.9)

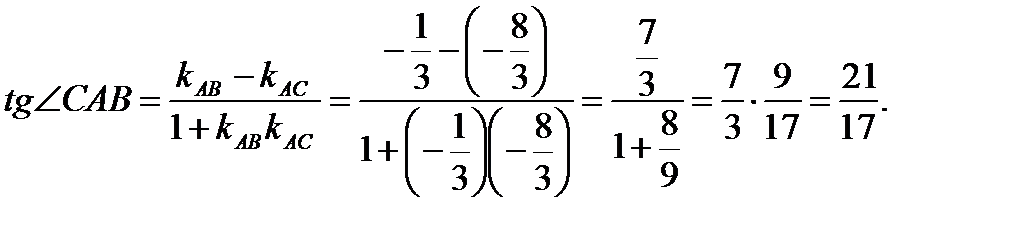
3. Чтобы найти уравнение высоты СК, необходимо использовать уравнение пучка прямых (1.5) и условие перпендикулярности двух прямых (1.11).

Прямая СК проходит через точку С и СК 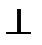 АВ.

Пучок прямых, проходящих через точку С(1;-5), по формуле (1.5) имеет вид

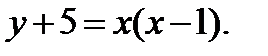
Угловой коэффициент прямой АВ: .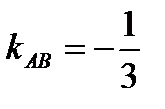

 На основании условия перпендикулярности двух прямых угловой коэффициент прямой СК

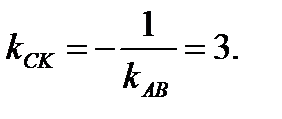
Уравнение прямой СК примет вид 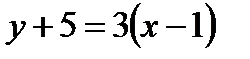или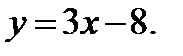

. Медиана СМ выходит из вершины С и делит противоположную сторону пополам, т.е. точка М является серединой отрезка АВ.

Координаты точки М вычислим по формулам (1.3).

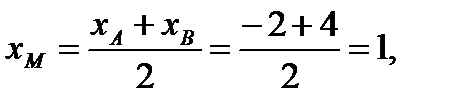
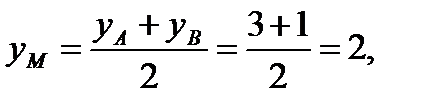           т.е. М(1;2).

Найдем уравнение прямой, проходящей через две точки С( 1; -5) и М(1;2). Поскольку абсциссы данных точек равны, прямая СМ параллельна оси Оу и ее уравнение х=1.

5. Чтобы найти точку пересечения высот, необходимо знать уравнения хотя бы двух высот треугольника. Уравнение высоты СК уже найдено. Аналогично получим уравнение высоты BN .

Прямая BN проходит через точку В(4; 1) и BN 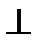 АС. Следовательно,

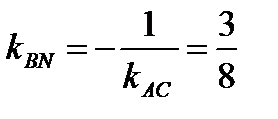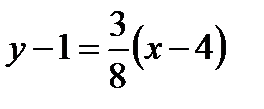            ,         или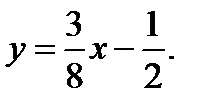

Координаты точки Р пересечения высот СК и BN найдем, решив систему уравнений

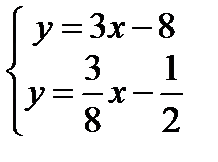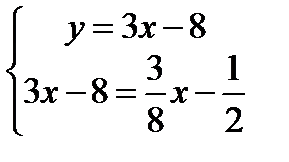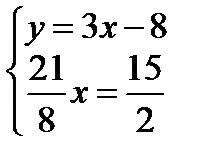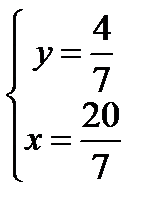, ,  ,   , т.е.

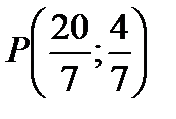- точка пересечения высот треугольника.

6. Длину высоты СК можно найти по формуле (1.12) расстояния отточки С(1;-5) до прямой х+3y -7 = 0 (АВ):

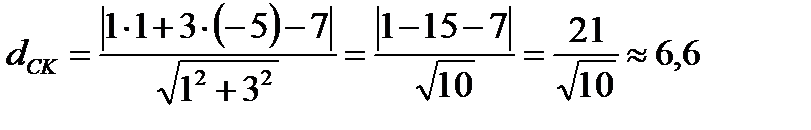
7. Для того, чтобы записать систему линейных неравенств, определяющих треугольник ABC , надо найти уравнения всех его сторон. Уравнения сторон АВ и АС уже известны. Аналогично найдем уравнение стороны ВС:

.

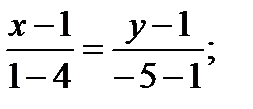
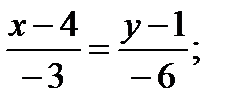
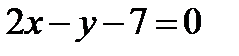- уравнение стороны ВС.

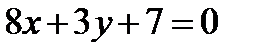- уравнение стороны АС.

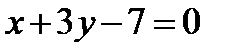 - уравнение стороны АВ.

Часть плоскости, определяющая треугольник ABC , заключена между прямыми АВ, АС, ВС и определяется системой линейных неравенств

.

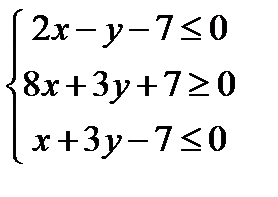Данные неравенства можно получить, подставив произвольную точку, лежащую внутри треугольника, в каждое уравнение прямой.