Определение. Функция F ( x ) называется первообразной функцией для функции 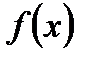 на промежутке X , если в каждой точке х этого промежутка

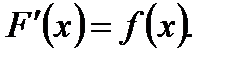
Определение. Совокупность всех первообразных для функции f ( x ) на промежутке X называется неопределенным интегралом от функции f(x), т.е.

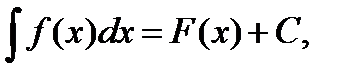
где F ( x ) - некоторая первообразная для f ( x ), С - произвольная постоянная.

Некоторые свойства неопределенного интеграла

1. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.

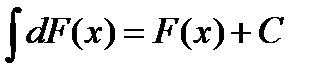                                                    (5.1)

2. Постоянный множитель можно выносить за знак интеграла, т.е.

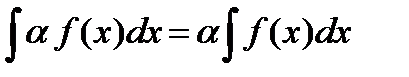,                   .                        (5.2)

где 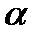 некоторое число.

3. Интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций, т.е

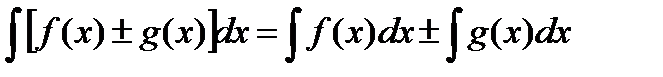                            (5.3)

Таблица неопределенных интегралов

1.

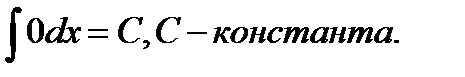
2.

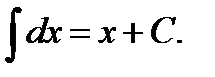
3.

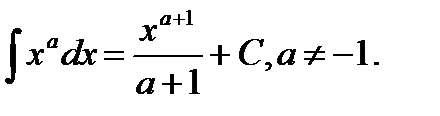
4.

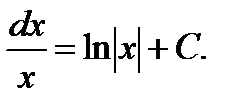
5.

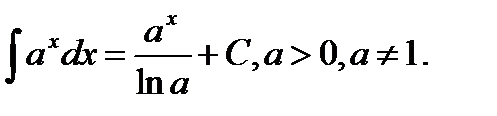
6.

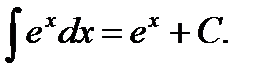
7.

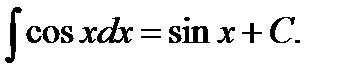
8.

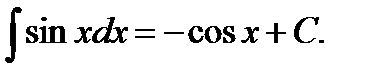
9.

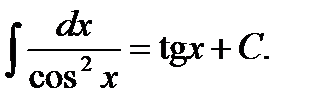
10.

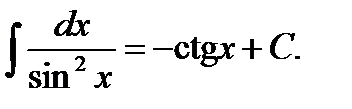
11.

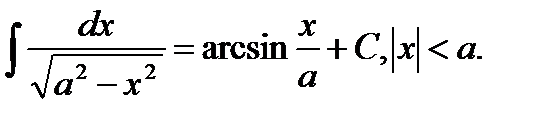
12.

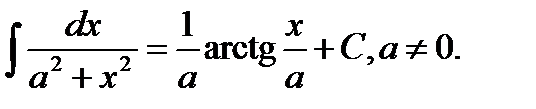
13.

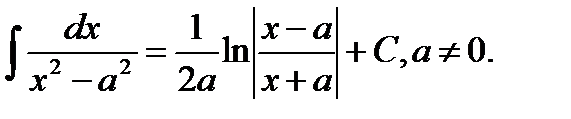
14.

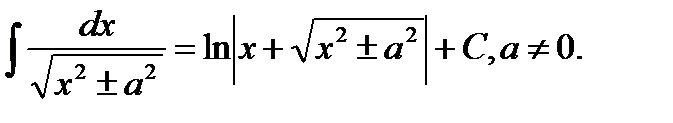
Метод замены переменной (метод подстановки)

На практике представленные в таблице интегралы от элементарных функций встречаются редко. Однако во многих случаях, сделав замену переменной в подынтегральной функции

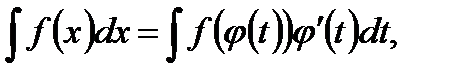
искомый интеграл можно привести к табличному виду.

Пример 1 . Найти интеграл .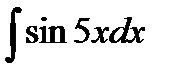

Решение. Сделаем замену: 5х = t . Дифференцируя это равенство, используя формулу df ( x )= f '( x ) dx , получаем 5 dx = dt , откуда dx = 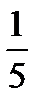dt . Подставляем в исходный интеграл:

.

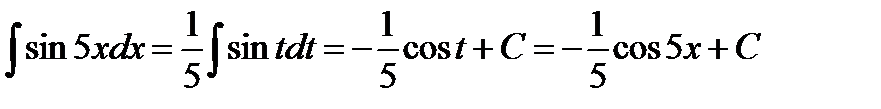Следует обратить внимание на то, что конечный результат должен выражаться не через переменную t , а через исходную переменную х.

Пример 2. Найти интеграл .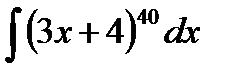

Решение. Сделаем замену: 3 x + 4 = t . Дифференцируя это равенство, получаем 3 dx = dt , dx = 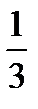dt . Тогда

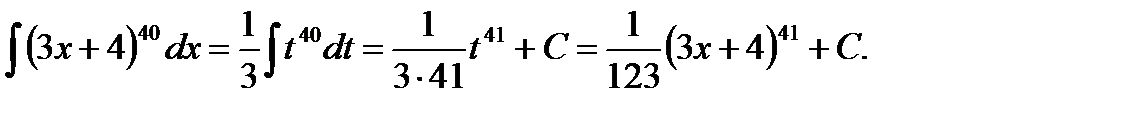
Проверим правильность полученного результата.

Так как операции дифференцирования и интегрирования - две взаимообратные операции, то, продифференцировав полученное выражение, мы должны получить подынтегральную функцию

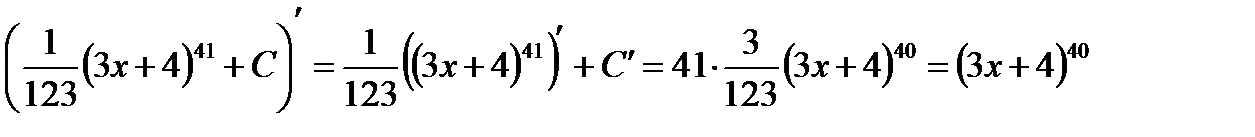
что совпадает с исходной подынтегральной функцией. Значит, интегрирование произведено правильно.

Пример 3 . Найти интеграл .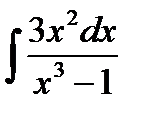

Решение. Нетрудно заметить, что в данном примере числитель дроби равен дифференциалу знаменателя. Это подсказывает замену: х³ -1=t.
Тогда d ( x³ -1) = dt , 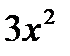dx = dt и, следовательно,

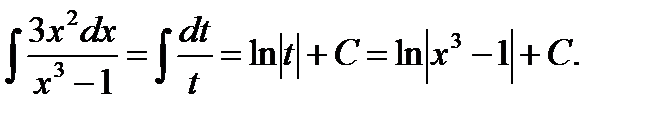
Пример 4 . Найти интеграл .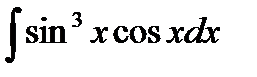

Решение. Сделаем замену: .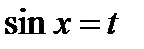
Тогда 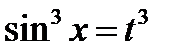   и 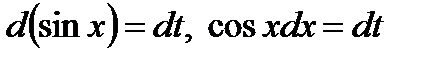. Таким образом,

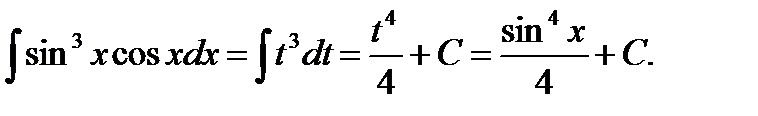
Метод интегрирования по частям

       Метод интегрирования по частям, так же как и метод замены переменной применяется с целью сведения данного интеграла к табличному.

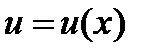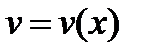Теорема. Если  и  - дифференцируемые функции, то

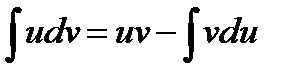
Пример 5. Найти интеграл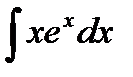

Решение. Полагая 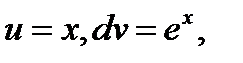 найдем необходимые для записи правой част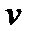и  и 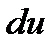. Так как  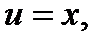то 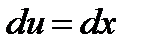. Согласно свойству 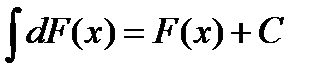, имеем 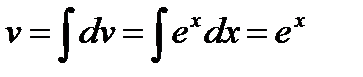. (Для упрощения записи решения полагаем С=0).