Функции, способы задания функций графики функций.
Числовой функцией называется зависимость одной переменной от другой такая, что каждому значению независимой переменной ставится в соответствие только одно значение зависимой.
Независимую переменную называют аргументом, зависимую - функцией.
Функцию можно задать таблицей ( в случае конечного числа значений аргумента), формулой, графиком.
Графиком функции являются все точки координатной плоскости, абсцисса которых значение аргумента функции, ордината - соответствующее значение функции.
Область определения функции ( Dy ) – множество всех допустимых значений аргумента.
Область значений функции ( Ey ) – множество значений которые может принимать функция.
Свойства функций (монотонность, четность, периодичность)
Функция f называется возрастающей на промежутке, если для любых значений аргументов 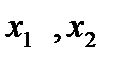 таких, что
таких, что 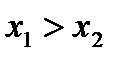
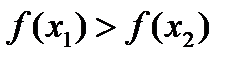 , т.е. большему значению аргумента соответствует большее значение функции.
, т.е. большему значению аргумента соответствует большее значение функции.
Функция f называется убывающей на промежутке, если для любых значений аргументов 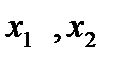 таких, что
таких, что 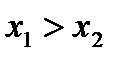
 , т.е. большему значению аргумента соответствует меньшее значение функции.
, т.е. большему значению аргумента соответствует меньшее значение функции.
Функция f называется четной, если 1)область определения функции симметрична относительно нуля, 2)для любого х из области определения 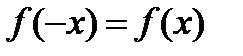 , т.е.значение функции от противоположных аргументов одинаково.
, т.е.значение функции от противоположных аргументов одинаково.
График четной функции симметричен относительно оси ординат.
Функция f называется нечетной, если 1)область определения функции симметрична относительно нуля, 2) для любого х из области определения 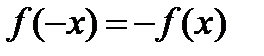 , т.е.значение функции от противоположных аргументов противоположно.
, т.е.значение функции от противоположных аргументов противоположно.
График нечетной функции симметричен относительно начала координат.
Функция f называется периодической с периодом Т 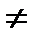 0, если для любого х из области определения
0, если для любого х из области определения 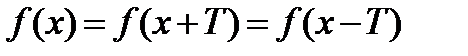 , т.е. значения функции в точках Х, х+Т, х-Т равны. 1) Если функция f периодическая и Т период , то kT так же являеся периодом этой функции. 2) Если функция f периодическая и Т период , то число
, т.е. значения функции в точках Х, х+Т, х-Т равны. 1) Если функция f периодическая и Т период , то kT так же являеся периодом этой функции. 2) Если функция f периодическая и Т период , то число 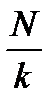 является периодом функции
является периодом функции 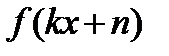
Преобразование графиков функций
| Функция вида | Преобразование графика | Пример | |
| 1 | y=-f(x) | Симметрия относительно оси ОХ | |
| 2 | y=f(-x) | Симметрия относительно оси ОУ | |
| 3 | y=f(x+a) | Параллельный перенос вдоль оси ОХ на –а единиц | |
| 4 | y=f(x)+b | Параллельный перенос вдоль оси ОУ на b единиц | |
| 5 | y=|f(x) | | Часть графика в верхней полуплоскости и на оси абсцисс без изменений, а вместо части графика в нижней полуплоскости строится симметричный ему относительно оси ОХ | |
| 6 | y=f(|x|) | Часть графика для х 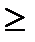 0 симметрично отображаем относительно оси ОУ 0 симметрично отображаем относительно оси ОУ
| |
| 7 | y=kf(x) (k>0) | При k>1 растяжение от точки (0;0) вдоль оси ОУ в k раз; при 0<k<1 сжатие к точке (0;0) вдоль оси ОУ в 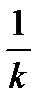 раз раз
| |
| 8 | y=f(kx) | При k>1 сжатие к точке (0;0) вдоль оси ОХ в k раз; при 0<k<1 растяжение от точки (0;0) вдоль оси ОХ в 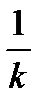 раз раз
|
Предел функции
Число А называется пределом функции в точке  или при
или при 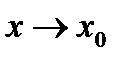 , если для любого числа
, если для любого числа 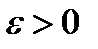 существует такое число
существует такое число 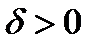 , такое что для всех х , которые удовлетворяют условию
, такое что для всех х , которые удовлетворяют условию 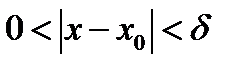 , справедливо неравенство
, справедливо неравенство 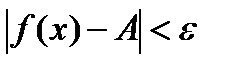 . (определение по Коши)
. (определение по Коши)
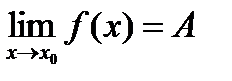
Если в определении предела рассматриваются только х<х0, то предел называется левосторонним и обозначается:
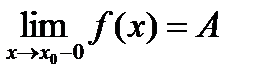
Если в определении предела рассматриваются только х>х0, то предел называется правосторонним и обозначается:
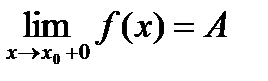
Свойства пределов функции:
1) если в некоторой точке из области определения существует предел
функции, то он единственный;
2) предел суммы равен сумме пределов
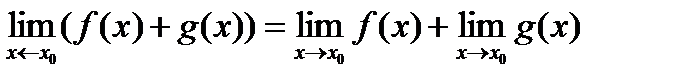 ;
;
3) предел произведения равен произведению пределов
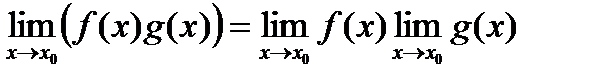 ;
;
4) предел частного равен частному пределов
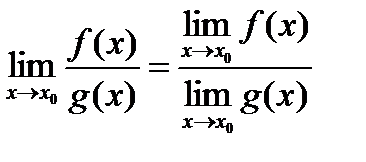 ;
;
Следствия:
1) постоянный множитель можно выносить за знак предела
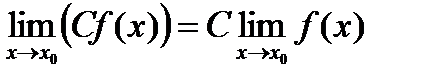 ;
;
2) если 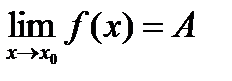 ,то
,то 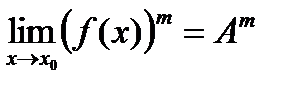 .
.
И 2 замечательные пределы
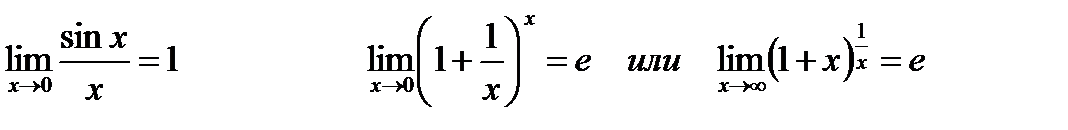
Непрерывность функции
Функция называется непрерывной в точке х0, если значение предела функции при 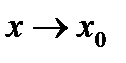 совпадает со значением функции в этой точке. Т.е. функция определена в точке х0, существует предел в этой точке и значение предела совпадает со значением функции.
совпадает со значением функции в этой точке. Т.е. функция определена в точке х0, существует предел в этой точке и значение предела совпадает со значением функции.
Невыполнение хотя бы одного из этих трех условий свидетельствует о наличии разрыва в данной тоске.
Функция называется непрерывной на промежутке, если она непрерывна в каждой точке промежутка.
Точка разрыва называется разрывом первого рода (скачком), если существует левосторонний и правосторонний пределы функции в точке, но они не равны.
В остальных случаях точка разрыва называется разрывом второго рода.
Дата: 2019-11-01, просмотров: 366.