Формулы дифференцирования элементарных функций

1) (с)'=0, где с - константа.

2) 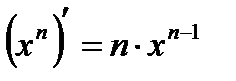,  где .

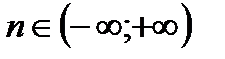В частности, ;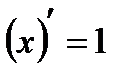   

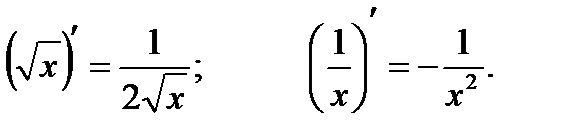
Правила дифференцирования

Пусть с - константа; u=u(х), v=v(x) - функции, имеющие производные, тогда

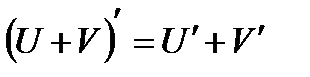;                                                         (3.1)

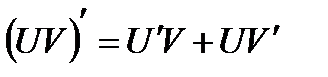;                                                        (3.2)

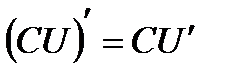;                                                                (3.3)

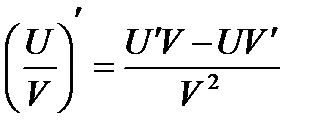 .                                                                   (3.4)

Замечание. Правило дифференцирования алгебраической суммы двух слагаемых распространяется на случай алгебраической суммы любого конечного числа слагаемых, т.е.

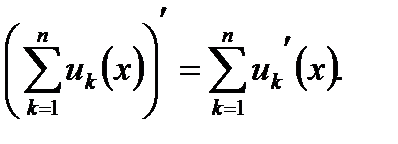
Производная сложной функции

Если 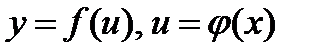- функции, имеющие производные, то производная сложной функции равна производной данной функции  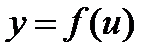по промежуточному аргументу и и умноженной на производную самого промежуточно­го аргумента  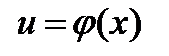 по независимой переменной х, т.е

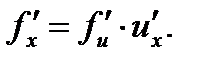                                                     (3.5)

Общая схема исследования функций и построения их графиков

1. Найти область определения функции.

2. Исследовать функцию на четность, периодичность.

3. Найти точки пересечения графика функции с осями координат.

4. Найти вертикальные асимптоты графика функции.

5. Исследовать поведение функции в бесконечности, найти горизонталь­ные или наклонные асимптоты.

6. Найти интервалы возрастания и убывания функции и ее экстремумы.

7. Найти интервалы выпуклости функции и ее точки перегиба.

8. Построить график функции, используя полученные результаты
исследования.

Задание 4

Найти производные функций:

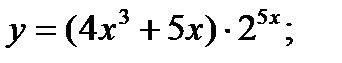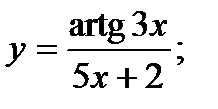a)      б)      в)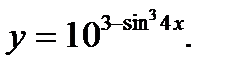

Решение

     а) Применяя правила дифференцирования суммы и произведения двух функций (3.1) и (3.2), формулы 1, 2, 3, формулу дифференцирования сложной функции (3.5), получим

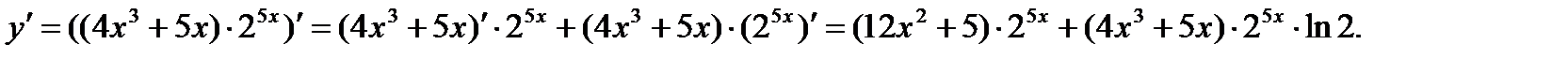
     б) Применяя правила (3.1)-(3.5), формулы 1,2, 11, получим:

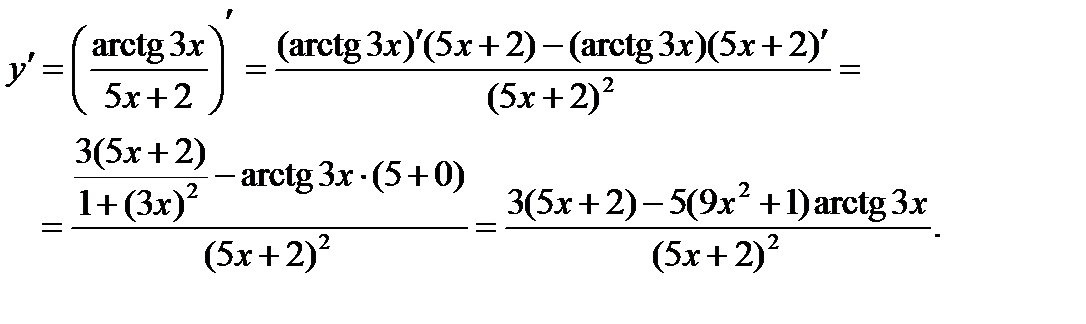
в) Применяя формулу дифференцирования сложной функции (3.5), правила (3.1), (3.3), формулы 1, 2, 3,5, получим:

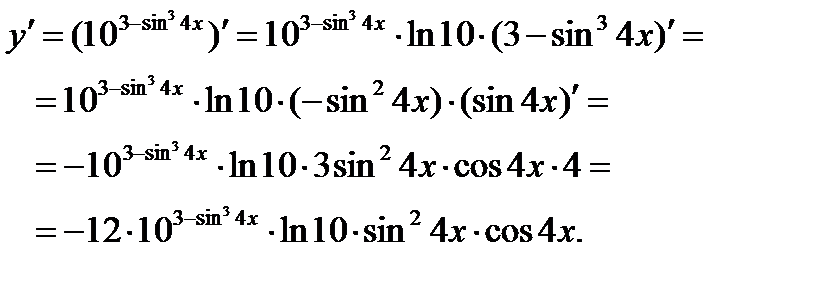
Задание 5

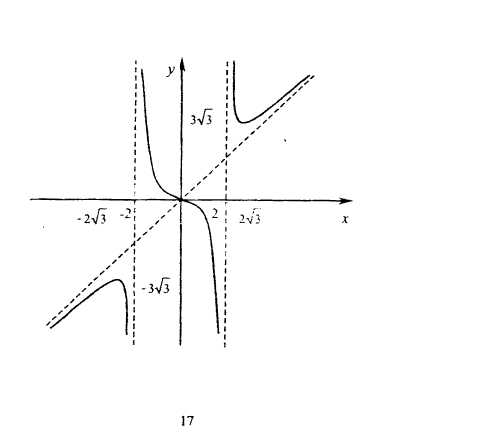
Исследовать функцию 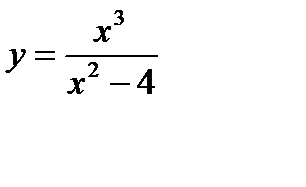 и построить ее график.

Решение

1. Функция определена при любом действительном значении аргумента х за исключением х= -2 и х=2. Следовательно, область определения данной функции .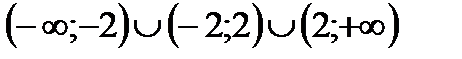

2. Так как 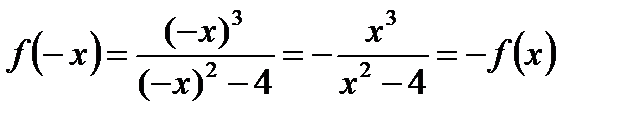, то данная функция нечетная и ее график симметричен относительно начала координат. На этом основании можно ограничиться исследованием и построением графика только для х 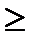0. Вторая часть графика (для х<0) может быть достроена по симметрии.

Функция не периодична.

3. Найдем точки пересечения с осями координат. f(0)=0. Уравнение f(х)=0 имеет единственное решение х = 0, т.е. график функции проходит через начало координат (0; 0). Других точек пересечения графика функции с осями координат нет.

4. Вертикальные асимптоты могут пересекать ось абсцисс в точках
х=± 2. Так как пределы функции при х→ 2-0 (слева) и при х→ 2+0 (справа) бесконечны, т.е.

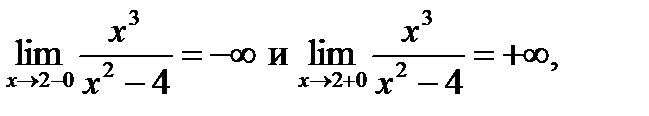то прямая х=2 есть вертикальная асимптота. В силу симметрии графика х= -2 также вертикальная асимптота.

5.  Поведение функции в бесконечности: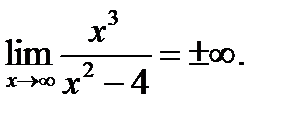

Следовательно, горизонтальных асимптот функция не имеет. Найдем наклонные асимптоты

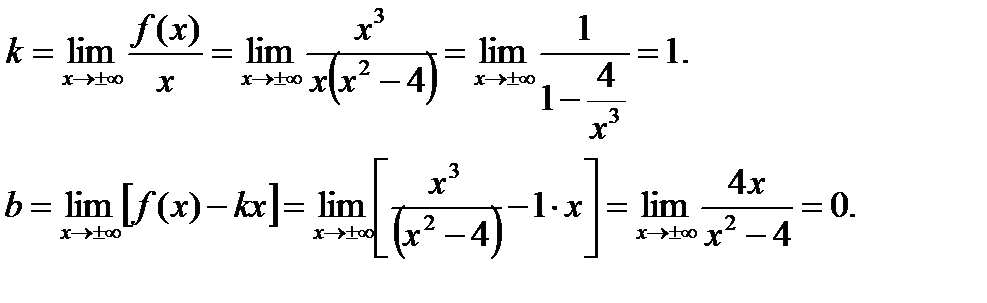
Подставим k=1 и b=0 в уравнение прямой у=кх+ b . Таким образом, наклонная асимптота графика функции имеет вид у= x

6. Интервалы монотонности и экстремумы. Найдем производную функции:

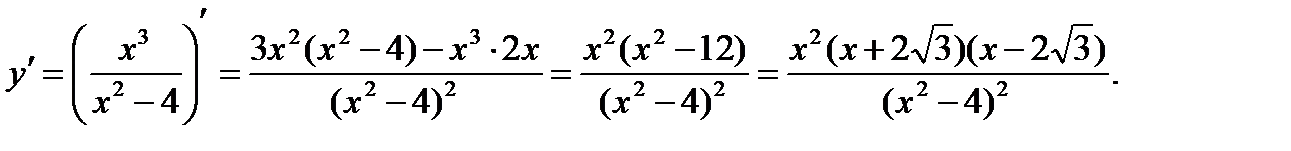
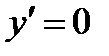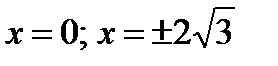 при , и 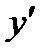 не существует при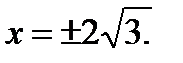

Однако критическими являются только точки 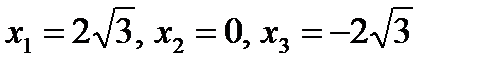 (так как значения х = ±2 не входят в область определения функции).

Исследуем на экстремум только точку 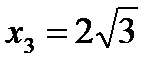(точки  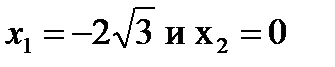на экстремум не исследуем, так как при симметричном достраивании графика вопрос об экстремуме в этих точках будет решен без использования достаточного условия).

Рассмотрим знаки 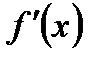 в интервалах  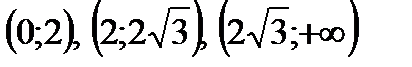и составим таблицу:

x		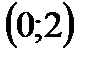2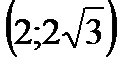
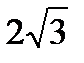
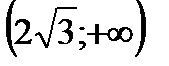
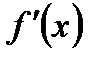
	-	не существует	-	0	+
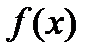
		не существует		min

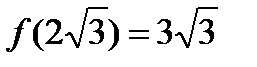
Из таблицы следует, что функция убывает пр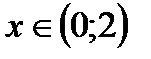и  и 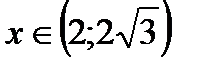, а возрастает при .

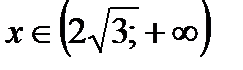Точка 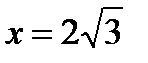- точка минимума и  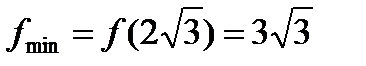- минимум функции.

7. Интервалы выпуклости и точки перегиба.

Найдем вторую производную

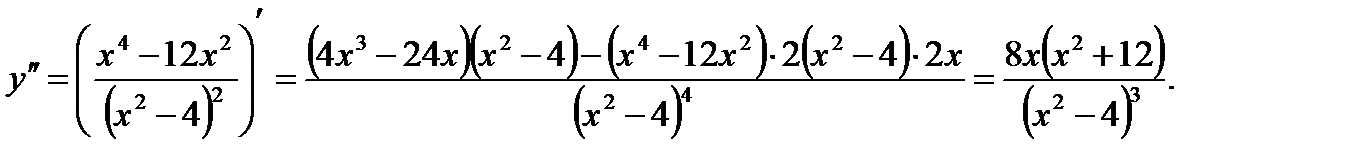
Вторая производная обращается в нуль при x = 0 и не существует при х = ±2, но точки х = ±2 не принадлежат области определения.

Рассмотрим знаки второй производной в интервалах (0;2),(2;+оо). При
х 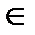(0;2)  у"<0 и график функции в этом интервале выпуклый вверх. При
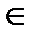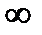х  (2;+ ) у">0 и график функции в этом интервале выпуклый вниз. Точка
х = 0 - точка перегиба в силу симметрии относительно начала координат.

8. Построим график функции для 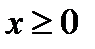 симметрично отобразим его относительно начала координат.