МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к изучению учебной дисциплины «Математика»
для студентов заочного отделения
2019
СОДЕРЖАНИЕ
Тема 1. Комплексные числа…………………………………………………..3
Тема 2. Аналитическая геометрия………………..…………………………..5
Тема 3. Функция и её свойства…………………………………………………...8
Функция. Свойства функций. Графики функций…………………………...9
Преобразование графиков функций…………………………………….10
Предел функции. 1 и 2 замечательные пределы………………………..11
Непрерывность функции. Точки разрыва………………………………11
Тема 4. Дифференциальное исчисление функции одной переменной …12
Формулы дифференцирования элементарных функций……………….12
Правила дифференцирования функций………………………………….13
Производная сложной функции………………………………………….14
Общая схема исследования функций и построения их графиков……..14
Тема 5. Неопределенный интеграл. Методы интегрирования………….17
Таблица простейших интегралов………………………………………...17
Метод замены переменной (метод подстановки)……………………….18
Метод интегрирования по частям………………………………………..19
Тема 6. Определенный интеграл …………………………………….………20
Геометрические приложения определенного интеграла………………20
Тема 7. Дифференциальные уравнения …………………………..………..22
Дифференциальные уравнения первого порядка с разделяющимися переменными…………………………………………………………………….22
Однородные дифференциальные уравнения первого порядка………..23
Линейные дифференциальные уравнения первого порядка…………..25
Список рекомендуемой литературы …….………………………………...27
Тема 1. КОМПЛЕКСНЫЕ ЧИСЛА
В связи с развитием алгебры потребовалось ввести сверх прежде известных положительных и отрицательных чисел числа нового рода. Они называются комплексными.
Комплексное число имеет вид a + bi; здесь a и b – действительные числа , а i – число нового рода, называемое мнимой единицей.
“Мнимые” числа составляют частный вид комплексных чисел
(когда а = 0). С другой стороны, и действительные числа являются частным видом комплексных чисел (когда b = 0).
Действительное число a назовем абсциссой комплексного числа a + bi; действительное число b – ординатой комплексного числа
a + bi. Основное свойство числа i состоит в том, что
i 2 = -1. (1)
Действительное число а записывается также в виде a + 0 i (или a – 0 i).
П р и м е р ы. Запись 3 + 0 i обозначает то же, что запись 3. Запись –2 + 0 i означает –2.
Комплексное число вида 0 + bi называется “чисто мнимым”. Запись bi обозначает то же, что 0 + bi .
Два комплексных a + bi , a ’ + b ’ i считаются равными, если у них соответственно равны абсциссы и ординаты.
Действия над комплексными числами в алгебраической форме
О п р е д е л е н и е. Суммой комплексных чисел a + bi и a ’ + b ’ i называют комплексное число ( a + a ’) + ( b + b ’) i.
Пример 1. (-3 + 5 i ) + (4 – 8 i ) = 1 - 3 i
Два комплексных числа a+bi и a-bi называются сопряженными. Сумма сопряженных комплексных чисел равна действительному числу.
О п р е д е л е н и е. Разностью комплексных чисел a + bi (уменьшаемое) и a ’ + b ’ i (вычитаемое) называется комплексное число ( a – a ’) + ( b – b ’) i.
Пример 1. (-5 + 2i) – (3 – 5i) = -8 + 7i
Пример 2. (3 + 2i) – (-3 + 2i) = 6 + 0i = 6
О п р е д е л е н и е. Произведением комплексных чисел a + bi и a ’ + b ’ i называется комплексное число
(aa’ – bb’) + (ab’ + ba’)i.
З а м е ч а н и е . На практике нет нужды пользоваться формулой произведения. Можно перемножить данные числа, как двучлены, а затем положить, что i 2 = -1.
Пример 1. (1 – 2i)(3 + 2i) = 3 – 6i + 2i – 4i 2 = 3 – 6i + 2i + 4 = 7 – 4i.
Пример 2. (a + bi)(a – bi) = a2 + b 2
О п р е д л е н и е. Разделить комплексное число a + bi на комплексное число a’ + b’i – значит найти такое число x + yi, которое, будучи помножено на делитель, даст делимое.
Если делитель не равен нулю, то деление всегда возможно, и частное единственно. На практике частное удобнее всего находить следующим образом.
Пример 1. Найти частное (7 – 4 i ):(3 + 2i).
Записав дробь (7 – 4 i )/(3 + 2 i), расширяем её на число 3 – 2 i, сопряженное с 3 + 2 i. Получим:
((7 – 4i)(3 - 2i))/((3 + 2i)(3 – 2i)) = (13 – 26i)/13 = 1 – 2i.
Пример 1. (-2 +5i)/(-3 –4i) = ((-2 + 5i)(-3 – 4i))/((-3 – 4i)( -3 + 4i)) = (-14 –23i)/25 = -0,56 – 0.92i.
Геометрическое изображение комплексных чисел.
Комплексные числа можно изобразить на числовой плоскости прямоугольную систему координат с одним и тем же масштабом на обеих осях. Комплексное число a + bi мы изображаем точкой М, у которой абсцисса х равна абсциссе а комплексного, а ордината у равна ординате b комплексного числа.
Комплексные можно изображать также векторами, начинающимися в точке О и оканчивающимися в соответствующей точке числовой плоскости. Так, комплексное число -2 + 6 i можно изобразить не только точкой В, но также вектором ОВ ; комплексное число
–6 – 2 i изображается вектором ОС и т. д.
В 6 у у
r b
q
О х a x
6 С
Модуль и аргумент комплексного числа.
Длина вектора, изображающего комплексное число, называется модулем этого комплексного числа. Модуль всякого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа a + bi обозначается | a + bi |, а также буквой r. Из чертежа видно, что
r = | a + bi | = a 2 + b 2
Модуль действительного числа совпадает с его абсолютным значением. Сопряжённые комплексные числа a + bi u a – bi имеют один и тот же модуль.
Тригонометрическая форма комплексного числа.
Абсцисса а и ордината b комплексного числа a + bi выражаются через модуль r и аргумент q. Формулами
a = r cos q; b = r sin q.
Поэтому всякое комплексное число можно представить в виде
r(cos q + i sin q), где r > 0.
Показательная форма комплексного числа
Комплексное число так же можно представить  в виде
в виде
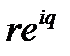
Основные формулы
Расстояние между двумя точками плоскости М1(x 1 , y 1) и М2(х2,у2)
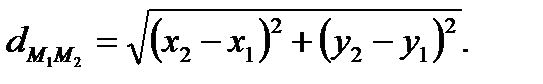 (1.1)
(1.1)
Координаты точки С, делящей отрезок АВ в отношении 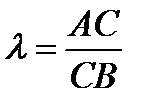
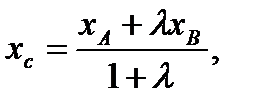
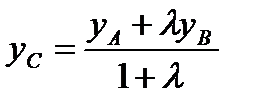 . (1.2)
. (1.2)
Если точка С является серединой отрезка АВ, то ее координаты
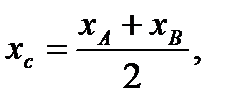
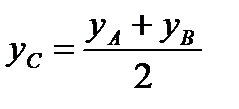 . (1.3)
. (1.3)
Уравнение прямой с угловым коэффициентом
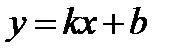 , (1.4)
, (1.4)
где 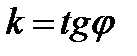 - угловой коэффициент.
- угловой коэффициент.
Уравнение прямой, проходящей через точку М1(х1 ,у1) в данном направлении
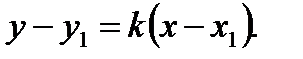 (1.5)
(1.5)
Если в уравнении (1.5) k — произвольное число, то это уравнение является уравнением пучка прямых, проходящих через точку М1( x 1 , y 1 ).
Уравнение прямой, проходящей через две точки М1(x 1 , y 1) и М2(х2,у)
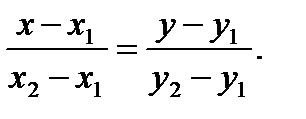 (1.6)
(1.6)
Уравнение прямой в отрезках
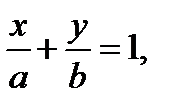 (1.7)
(1.7)
где a и b- отрезки, отсекаемые прямой на осях Ох и Оу соответственно.
Общее уравнение прямой
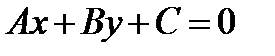 . (1.8)
. (1.8)
Угол а между двумя прямыми 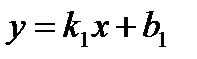 (I) и
(I) и 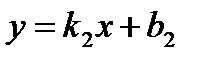 (II)
(II)
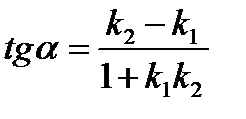 , (1.9)
, (1.9)
где стрелка означает, что угол 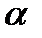 получается поворотом прямой (I)
получается поворотом прямой (I)
к прямой (II) против часовой стрелки.
Условие параллельности прямых 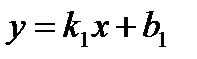 и
и 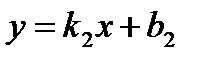
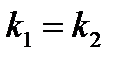 (1.10)
(1.10)
Условие перпендикулярности прямых 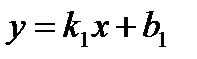 и
и 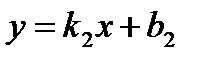
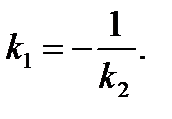 (1.11)
(1.11)
Расстояние от точки Мо (хо,уо) до прямой Ах + By + С=0
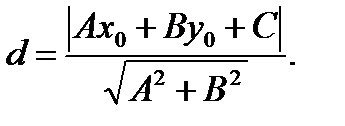 (1.12)
(1.12)
Координаты точки пересечения двух прямых находятся путем решения системы уравнений этих прямых.
Задание 1
Решение
1. Длину стороны АВ найдем по формуле (1.1), расстояния между двумя точками A(-2;3) и B(4; 1):
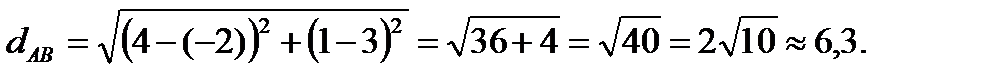
2. Внутренний угол А треугольника ABC можно найти по формуле (1.9). Но нам неизвестны угловые коэффициенты прямых АС и АВ. Найдем уравнения данных прямых, воспользовавшись уравнением прямой, проходящей через две данные точки. По формуле (1.6)
AC : 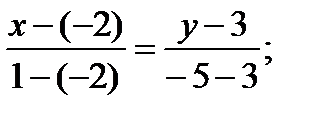
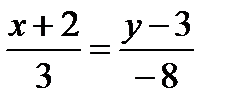 ;
;
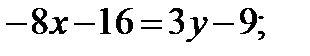
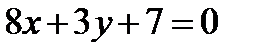 или
или
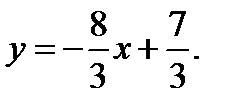
AB: 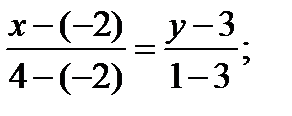
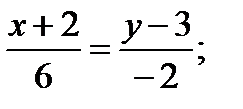
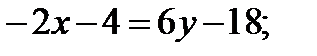
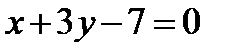 или
или
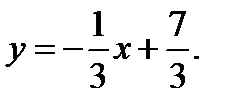
Из уравнений данных прямых следует, что их угловые коэффициенты
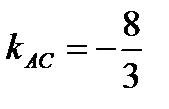 ,
, 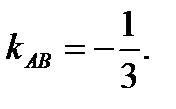
Теперь по формуле (1.9)
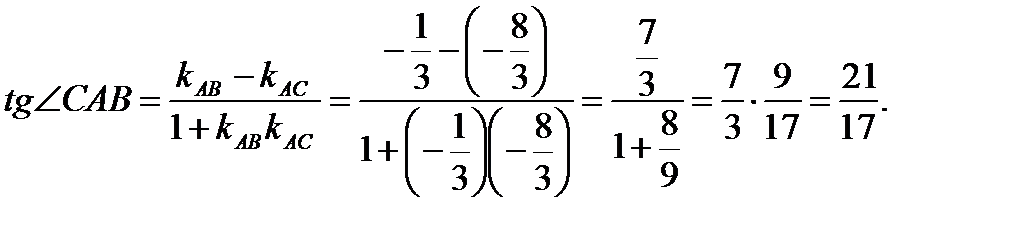
3. Чтобы найти уравнение высоты СК, необходимо использовать уравнение пучка прямых (1.5) и условие перпендикулярности двух прямых (1.11).
Прямая СК проходит через точку С и СК 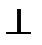 АВ.
АВ.
Пучок прямых, проходящих через точку С(1;-5), по формуле (1.5) имеет вид

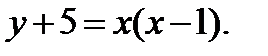
Угловой коэффициент прямой АВ: 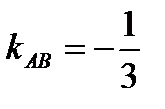 .
.
На основании условия перпендикулярности двух прямых угловой коэффициент прямой СК
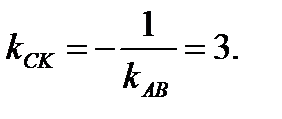
Уравнение прямой СК примет вид 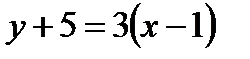 или
или 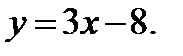
. Медиана СМ выходит из вершины С и делит противоположную сторону пополам, т.е. точка М является серединой отрезка АВ.
Координаты точки М вычислим по формулам (1.3).
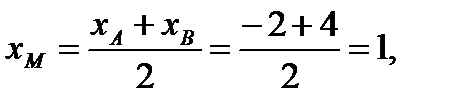
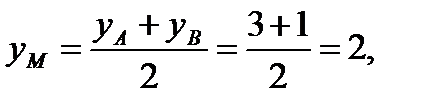 т.е. М(1;2).
т.е. М(1;2).
Найдем уравнение прямой, проходящей через две точки С( 1; -5) и М(1;2). Поскольку абсциссы данных точек равны, прямая СМ параллельна оси Оу и ее уравнение х=1.
5. Чтобы найти точку пересечения высот, необходимо знать уравнения хотя бы двух высот треугольника. Уравнение высоты СК уже найдено. Аналогично получим уравнение высоты BN .
Прямая BN проходит через точку В(4; 1) и BN 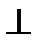 АС. Следовательно,
АС. Следовательно,
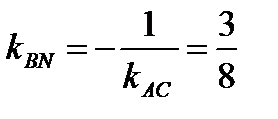 ,
, 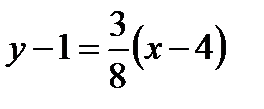 или
или 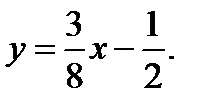
Координаты точки Р пересечения высот СК и BN найдем, решив систему уравнений
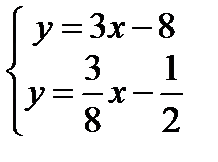 ,
, 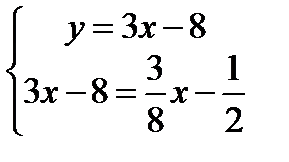 ,
, 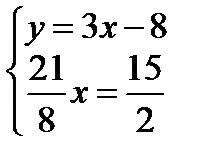 ,
, 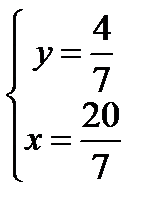 , т.е.
, т.е.
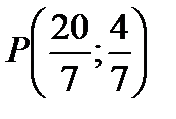 - точка пересечения высот треугольника.
- точка пересечения высот треугольника.
6. Длину высоты СК можно найти по формуле (1.12) расстояния отточки С(1;-5) до прямой х+3y -7 = 0 (АВ):
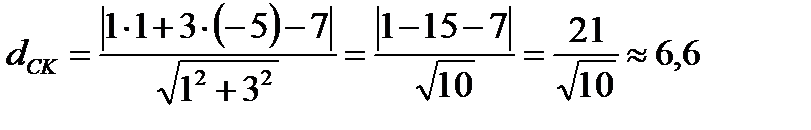
7. Для того, чтобы записать систему линейных неравенств, определяющих треугольник ABC , надо найти уравнения всех его сторон. Уравнения сторон АВ и АС уже известны. Аналогично найдем уравнение стороны ВС:
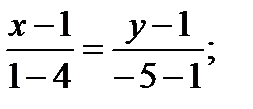
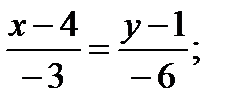
 .
.
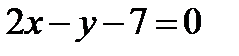 - уравнение стороны ВС.
- уравнение стороны ВС.
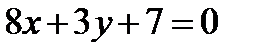 - уравнение стороны АС.
- уравнение стороны АС.
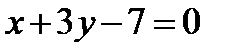 - уравнение стороны АВ.
- уравнение стороны АВ.
Часть плоскости, определяющая треугольник ABC , заключена между прямыми АВ, АС, ВС и определяется системой линейных неравенств
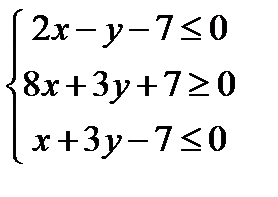 .
.
Данные неравенства можно получить, подставив произвольную точку, лежащую внутри треугольника, в каждое уравнение прямой.
И 2 замечательные пределы
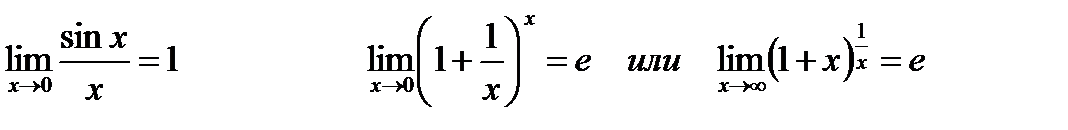
Непрерывность функции
Функция называется непрерывной в точке х0, если значение предела функции при 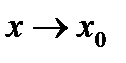 совпадает со значением функции в этой точке. Т.е. функция определена в точке х0, существует предел в этой точке и значение предела совпадает со значением функции.
совпадает со значением функции в этой точке. Т.е. функция определена в точке х0, существует предел в этой точке и значение предела совпадает со значением функции.
Невыполнение хотя бы одного из этих трех условий свидетельствует о наличии разрыва в данной тоске.
Функция называется непрерывной на промежутке, если она непрерывна в каждой точке промежутка.
Точка разрыва называется разрывом первого рода (скачком), если существует левосторонний и правосторонний пределы функции в точке, но они не равны.
В остальных случаях точка разрыва называется разрывом второго рода.
Правила дифференцирования
Пусть с - константа; u=u(х), v=v(x) - функции, имеющие производные, тогда
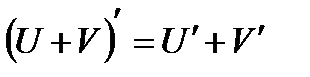 ; (3.1)
; (3.1)
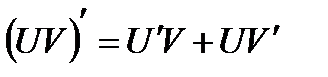 ; (3.2)
; (3.2)
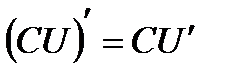 ; (3.3)
; (3.3)
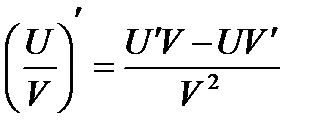 . (3.4)
. (3.4)
Замечание. Правило дифференцирования алгебраической суммы двух слагаемых распространяется на случай алгебраической суммы любого конечного числа слагаемых, т.е.
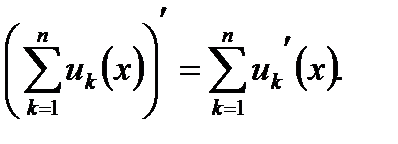
Производная сложной функции
Если 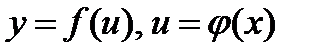 - функции, имеющие производные, то производная сложной функции равна производной данной функции
- функции, имеющие производные, то производная сложной функции равна производной данной функции 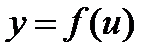 по промежуточному аргументу и и умноженной на производную самого промежуточного аргумента
по промежуточному аргументу и и умноженной на производную самого промежуточного аргумента 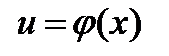 по независимой переменной х, т.е
по независимой переменной х, т.е
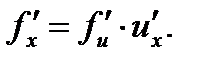 (3.5)
(3.5)
Общая схема исследования функций и построения их графиков
1. Найти область определения функции.
2. Исследовать функцию на четность, периодичность.
3. Найти точки пересечения графика функции с осями координат.
4. Найти вертикальные асимптоты графика функции.
5. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.
6. Найти интервалы возрастания и убывания функции и ее экстремумы.
7. Найти интервалы выпуклости функции и ее точки перегиба.
8. Построить график функции, используя полученные результаты
исследования.
Задание 4
Найти производные функций:
a) 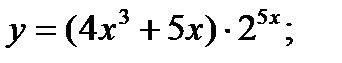 б)
б) 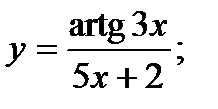 в)
в) 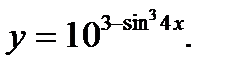
Решение
а) Применяя правила дифференцирования суммы и произведения двух функций (3.1) и (3.2), формулы 1, 2, 3, формулу дифференцирования сложной функции (3.5), получим
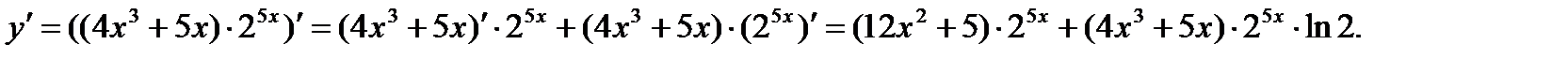
б) Применяя правила (3.1)-(3.5), формулы 1,2, 11, получим:
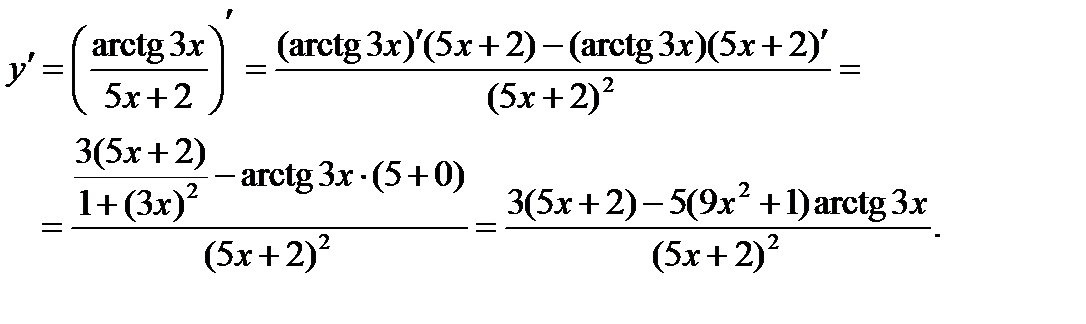
в) Применяя формулу дифференцирования сложной функции (3.5), правила (3.1), (3.3), формулы 1, 2, 3,5, получим:
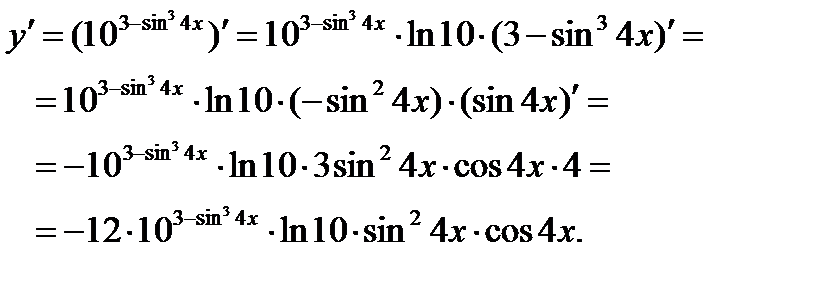
Задание 5
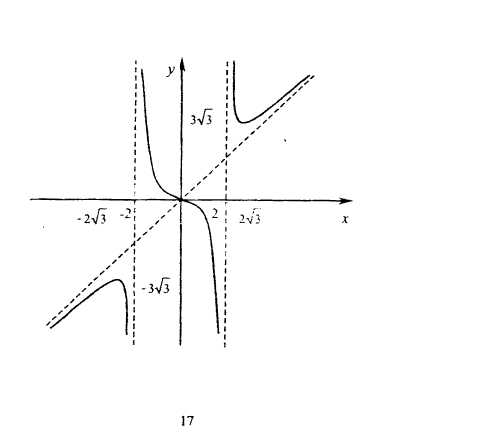
Исследовать функцию 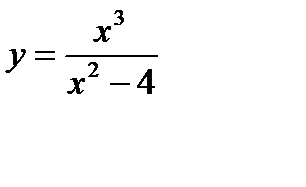 и построить ее график.
и построить ее график.
Решение
1. Функция определена при любом действительном значении аргумента х за исключением х= -2 и х=2. Следовательно, область определения данной функции 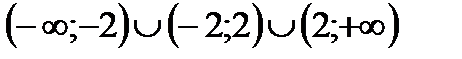 .
.
2. Так как 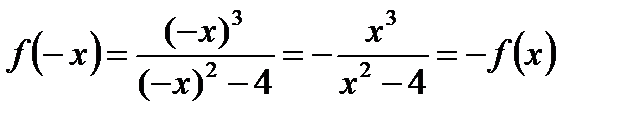 , то данная функция нечетная и ее график симметричен относительно начала координат. На этом основании можно ограничиться исследованием и построением графика только для х
, то данная функция нечетная и ее график симметричен относительно начала координат. На этом основании можно ограничиться исследованием и построением графика только для х 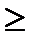 0. Вторая часть графика (для х<0) может быть достроена по симметрии.
0. Вторая часть графика (для х<0) может быть достроена по симметрии.
Функция не периодична.
3. Найдем точки пересечения с осями координат. f(0)=0. Уравнение f(х)=0 имеет единственное решение х = 0, т.е. график функции проходит через начало координат (0; 0). Других точек пересечения графика функции с осями координат нет.
4. Вертикальные асимптоты могут пересекать ось абсцисс в точках
х=± 2. Так как пределы функции при х→ 2-0 (слева) и при х→ 2+0 (справа) бесконечны, т.е.
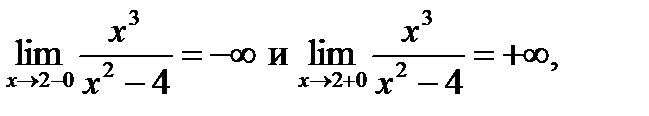 то прямая х=2 есть вертикальная асимптота. В силу симметрии графика х= -2 также вертикальная асимптота.
то прямая х=2 есть вертикальная асимптота. В силу симметрии графика х= -2 также вертикальная асимптота.
5. Поведение функции в бесконечности: 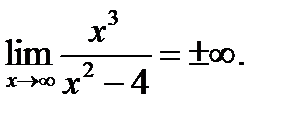
Следовательно, горизонтальных асимптот функция не имеет. Найдем наклонные асимптоты
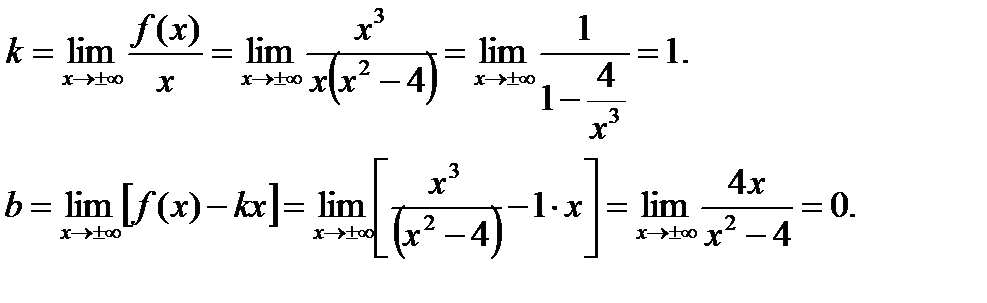
Подставим k=1 и b=0 в уравнение прямой у=кх+ b . Таким образом, наклонная асимптота графика функции имеет вид у= x
6. Интервалы монотонности и экстремумы. Найдем производную функции:
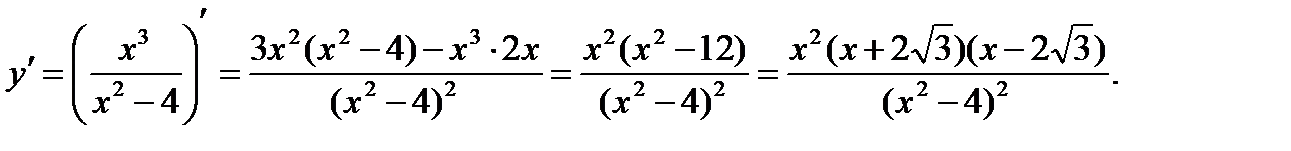
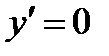 при
при 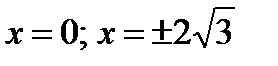 , и
, и 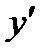 не существует при
не существует при 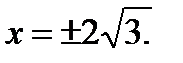
Однако критическими являются только точки 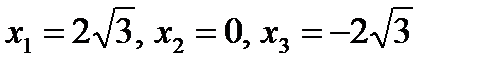 (так как значения х = ±2 не входят в область определения функции).
(так как значения х = ±2 не входят в область определения функции).
Исследуем на экстремум только точку 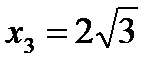 (точки
(точки 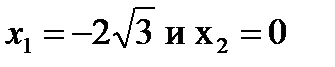 на экстремум не исследуем, так как при симметричном достраивании графика вопрос об экстремуме в этих точках будет решен без использования достаточного условия).
на экстремум не исследуем, так как при симметричном достраивании графика вопрос об экстремуме в этих точках будет решен без использования достаточного условия).
Рассмотрим знаки 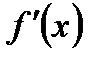 в интервалах
в интервалах 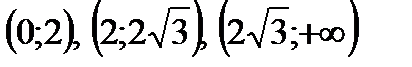 и составим таблицу:
и составим таблицу:
| x | 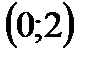
| 2 | 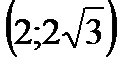
| 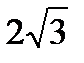
| 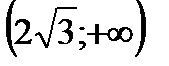
|
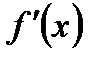
| - | не существует | - | 0 | + |
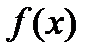
| не существует | min
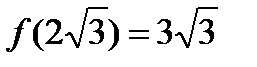
|
Из таблицы следует, что функция убывает при 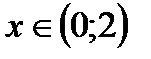 и
и 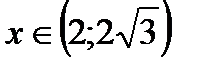 , а возрастает при
, а возрастает при 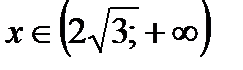 .
.
Точка 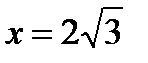 - точка минимума и
- точка минимума и 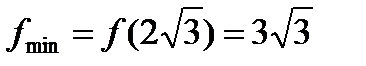 - минимум функции.
- минимум функции.
7. Интервалы выпуклости и точки перегиба.
Найдем вторую производную
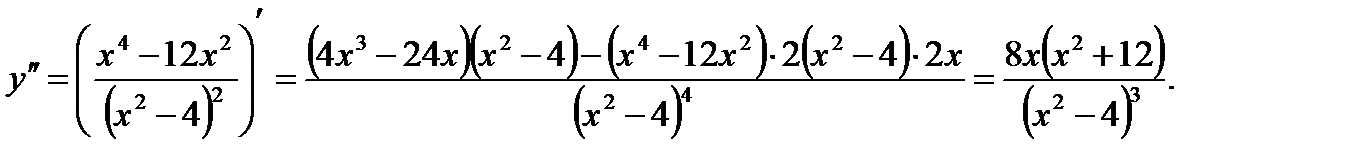
Вторая производная обращается в нуль при x = 0 и не существует при х = ±2, но точки х = ±2 не принадлежат области определения.
Рассмотрим знаки второй производной в интервалах (0;2),(2;+оо). При
х 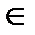 (0;2) у"<0 и график функции в этом интервале выпуклый вверх. При
(0;2) у"<0 и график функции в этом интервале выпуклый вверх. При
х 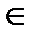 (2;+
(2;+ 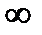 ) у">0 и график функции в этом интервале выпуклый вниз. Точка
) у">0 и график функции в этом интервале выпуклый вниз. Точка
х = 0 - точка перегиба в силу симметрии относительно начала координат.
|
|
8. Построим график функции для 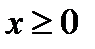 симметрично отобразим его относительно начала координат.
симметрично отобразим его относительно начала координат.
Таблица неопределенных интегралов
1. 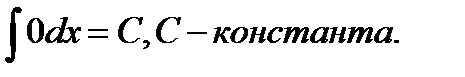
2. 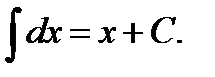
3. 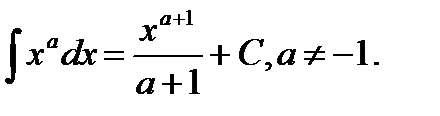
4. 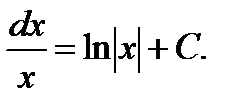
5. 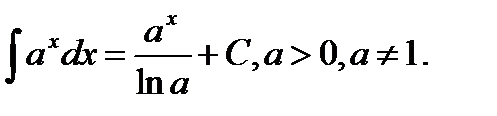
6. 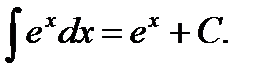
7. 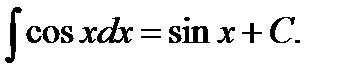
8. 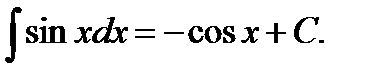
9. 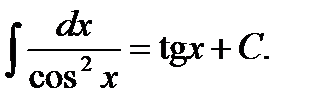
10. 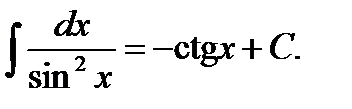
11. 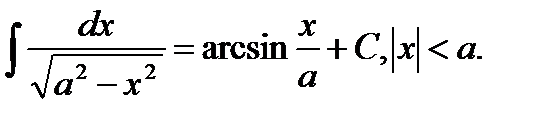
12. 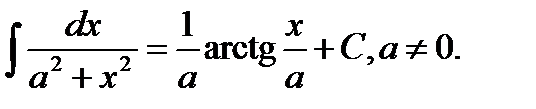
13. 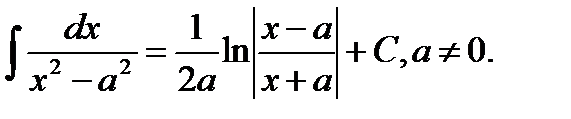
14. 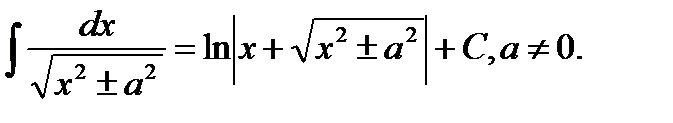
Решение.
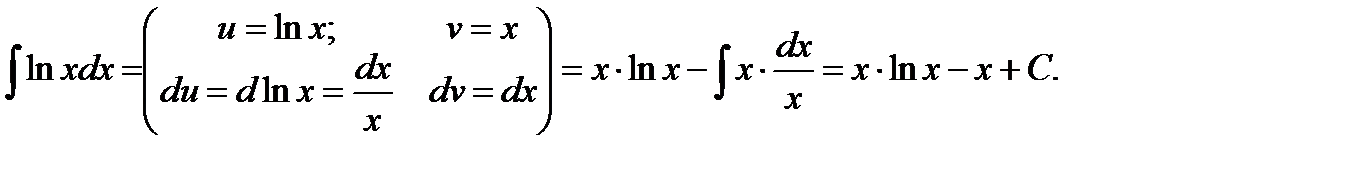
Пример 3. Найти интеграл 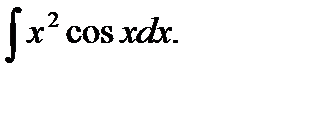
Решение.
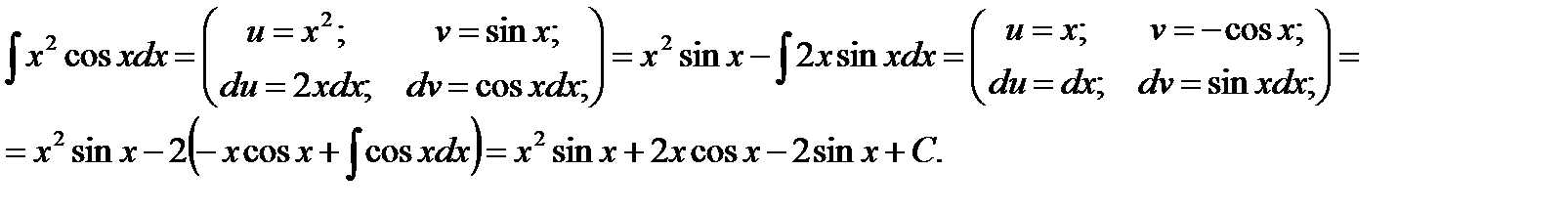
Задание
а) Вычислить объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линиями: 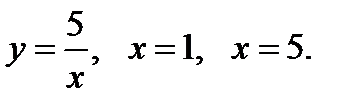
Решение
Изобразим на чертеже фигуру, объем которой требуется найти.
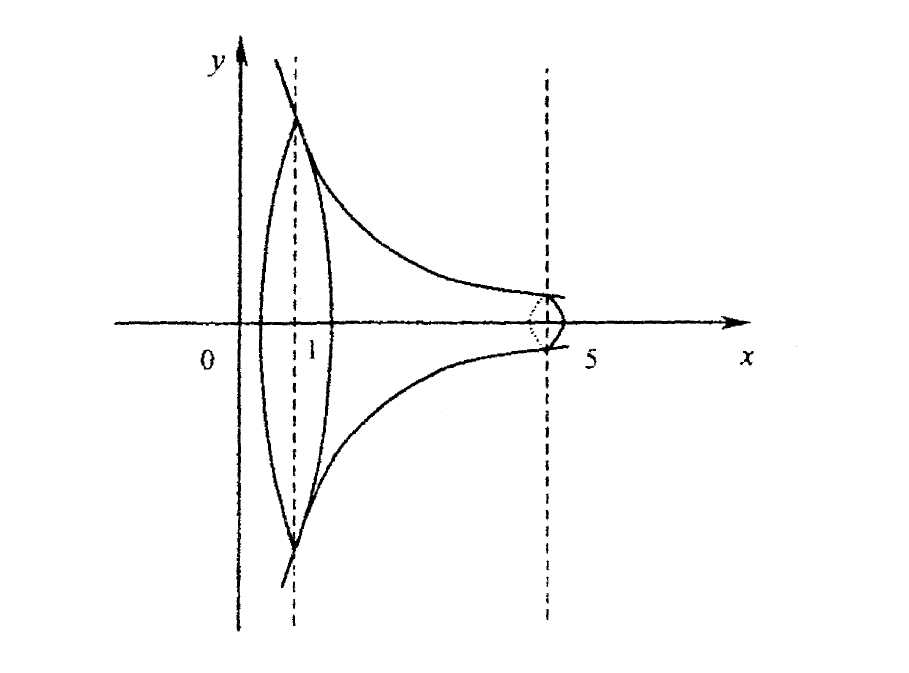
Так как полученная фигура вращается вокруг оси Ох, то воспользуемся формулой (6.2)
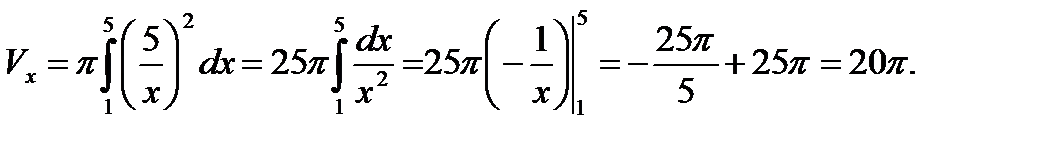
(см. (6.1)).
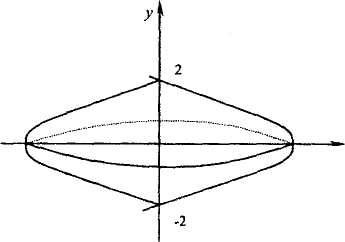
б) Вычислить объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной линиями: 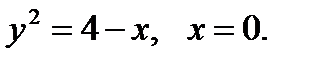
|
|
Решение
Изобразим на чертеже фигуру, объем которой требуется найти.
Так как полученная фигура вращается вокруг оси Оу, то запишем уравнение линии у2=4-х в виде х = 4-у2 и воспользуемся формулой (6.3).
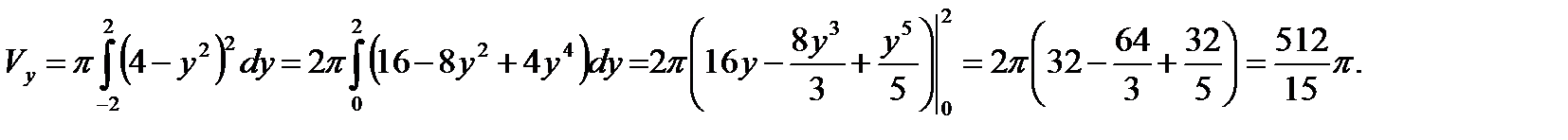
Тема 8. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Уравнение вида
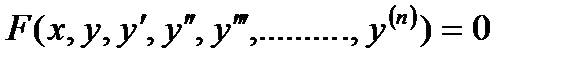 , (7.1)
, (7.1)
связывающее независимую переменную х, искомую функцию 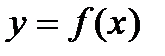 и ее производные различных порядков, называется обыкновенным дифференциальным уравнением.
и ее производные различных порядков, называется обыкновенным дифференциальным уравнением.
Порядок п старшей производной, входящей в запись уравнения называется порядком дифференциального уравнения.
Уравнение, содержащее производные или дифференциалы не выше первого порядка, называется дифференциальным уравнением первого порядка.
Решением дифференциального уравнения (7.1) называется функция 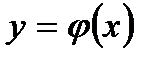 , которая, будучи подставлена в уравнение (7.1), обращает его в тождество.
, которая, будучи подставлена в уравнение (7.1), обращает его в тождество.
Процесс нахождения решения некоторого дифференциального уравнения называется интегрированием данного дифференциального уравнения.
Общим решением дифференциального уравнения (7.1) п-ого порядка называется такое его решение
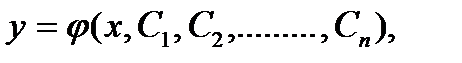
которое является функцией переменной х и п произвольных независимых постоянных  . (Независимость постоянных означает отсутствие каких-либо соотношений между ними).
. (Независимость постоянных означает отсутствие каких-либо соотношений между ними).
Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных  .
.
Пример 1.
Решить уравнение 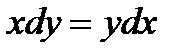 .
.
Решение.
Для разделения переменных обе части уравнения поделим на произведение ху, получим:
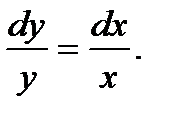
Интегрируя обе части последнего уравнения, найдем:
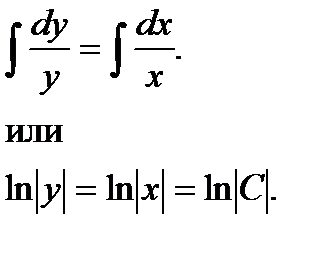
В правой части прибавлено постоянное в виде 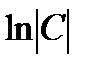 для облегчения потенцирования. Освобождаясь от символа логарифма, т.е. потенцируя, получим:
для облегчения потенцирования. Освобождаясь от символа логарифма, т.е. потенцируя, получим:
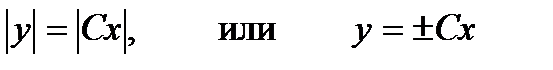 .
.
Пример 2.
Решить уравнение 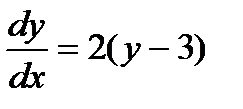 , если при
, если при 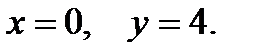
Решение.
После разделения переменных получим
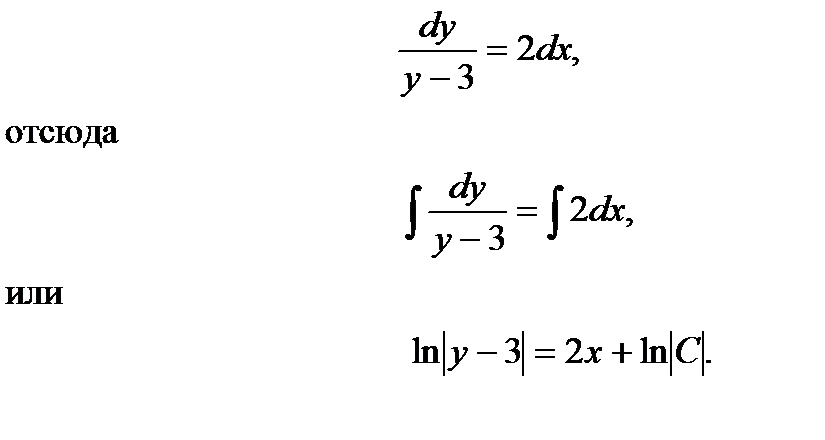
Для потенцирования нужно и правую часть последнего равенства написать со знаком логарифма. Согласно определения логарифма имеем:
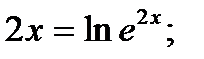
Следовательно, общее решение можно переписать в виде
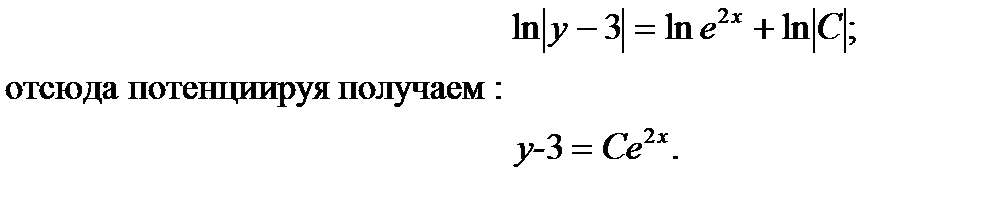
Находим значение С из условия 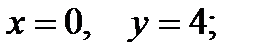 сделав подстановку, получим:
сделав подстановку, получим:
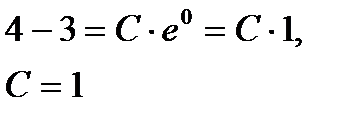
Итак, 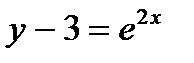 или
или 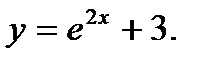
Пример 3.
Решить уравнение
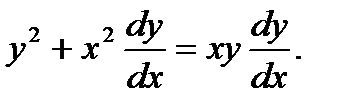 (1)
(1)
Решение.
Приведем уравнение, к стандартному виду умножив обе части его на 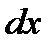 .
.
Получим:
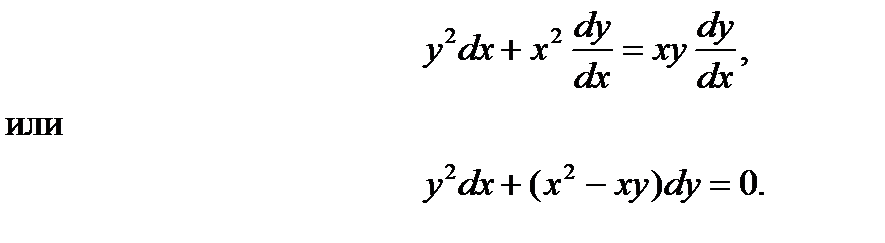 (2)
(2)
В данном уравнении 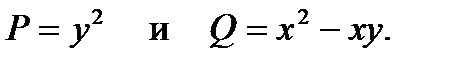
Как видно, 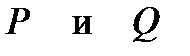 - однородные функции х и у , причем обе функции второй степени; поэтому уравнение однородное.
- однородные функции х и у , причем обе функции второй степени; поэтому уравнение однородное.
Из уравнения (1) находим
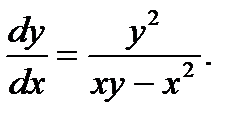 (3)
(3)
Положим
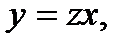 (4)
(4)
Где z – новая функция х. Найдя z , мы получим из равенства (4) искомую функцию у .
Для отыскания z продифференцируем по х равенство (4):
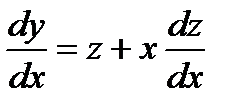 . (5)
. (5)
Подставим в уравнение (3) значения у и 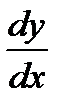 , взятые из равенств (4) и (5); получим
, взятые из равенств (4) и (5); получим
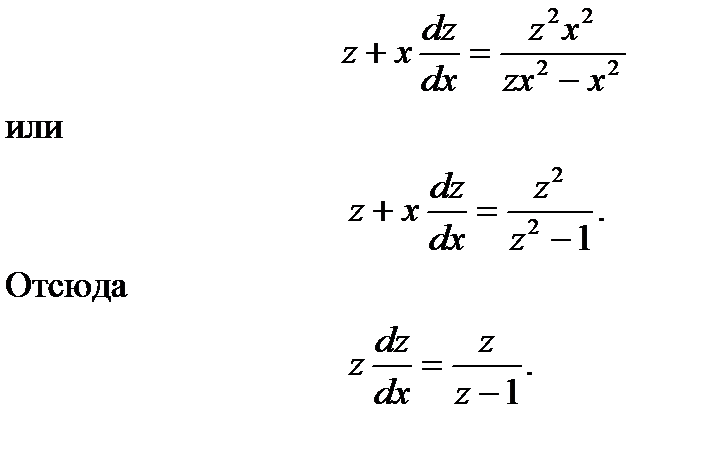
Произведя разделение переменных в полученном уравнении, напишем
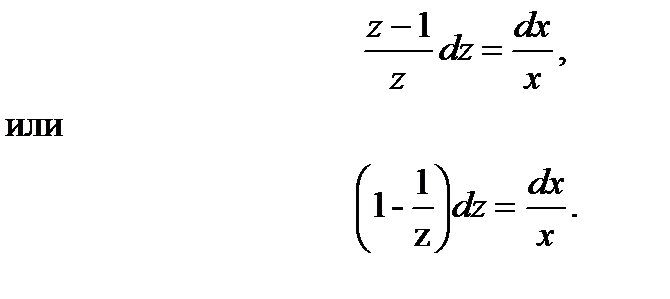
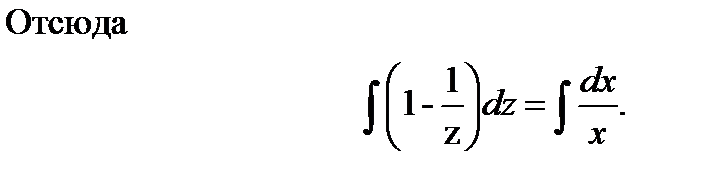
После интегрирования получим
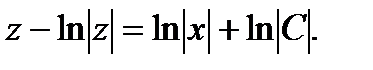 (6)
(6)
Представим z в виде
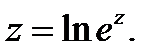
Теперь уравнение (6)примет вид
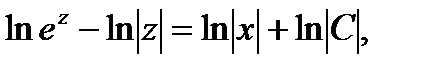
или
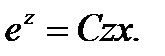 (7)
(7)
Из равенства (4) находим
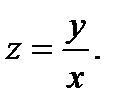
Заменив в равенстве (7) z найденным его значением, получим
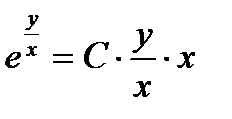
или
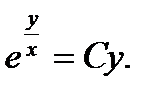 (8)
(8)
Уравнение (8) общее решение.
Замечание. Для проверки правильности решения уравнения дифференцируем по х обе части уравнения (8).
Пример 4.
Решить уравнение
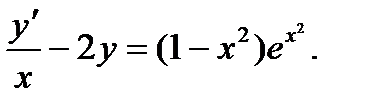
Решение.
Прежде всего нужно привести данное уравнение к виду (8.3), для этого умножим обе его части на х. получим
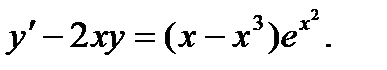 (1)
(1)
Положим 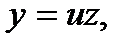 (2)
(2)
Где 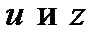 - новые функции х. наша задача – найти эти функции, чтобы затем найти искомую функцию у. продифференцируем по х равенство (2):
- новые функции х. наша задача – найти эти функции, чтобы затем найти искомую функцию у. продифференцируем по х равенство (2):
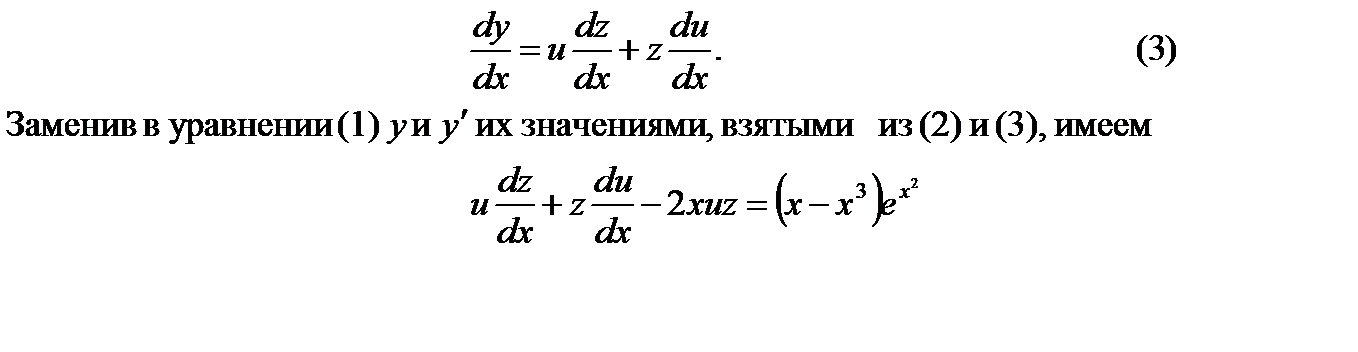
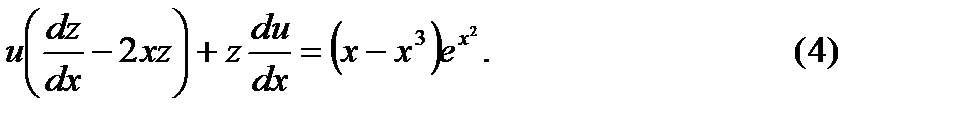
Найдем теперь такую функцию z, чтобы она обращала в нуль первую скобку в равенстве (4), т.е. чтобы
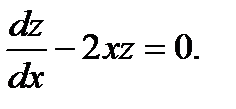 (5)
(5)
При этом условии уравнение (4) обратится в следующее:
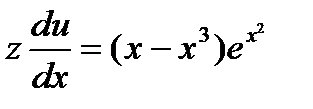 . (6)
. (6)
Произведя разделение переменных в уравнении (5), напишем
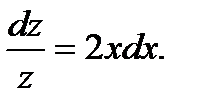 (7)
(7)
Отсюда

Нам нужно одно из частных решений уравнения (7). Выберем простейшее из них; с этой целью положим произвольное постоянное С=1. В результате имеем
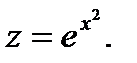 (9)
(9)
Подставив найденное значение z в уравнение (6), получим
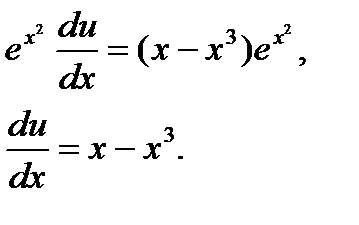
Это уравнение тоже с разделяющимися переменными. Решив его, найдем
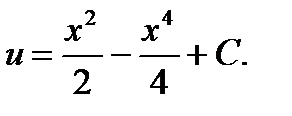 (10)
(10)
Подставив в равенстве (2) значения 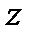 и
и 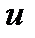 , взятые из равенств (9) и (10), получим общее решение уравнения (1)
, взятые из равенств (9) и (10), получим общее решение уравнения (1)
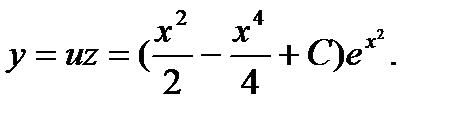
Проверка этого решения производится путем дифференцирования обеих частей полученного решения.
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы
Основная
1.Богомолов Н.В., Математика: учебное пособие для ссузов – М.: Дрофа, 2014
2 Бродский Я.С., Павлов А.Л., Слипенко А.К., Математика: Учебник.- К.: Высшая школа, 2005
3 Бродский Я.С., Павлов А.Л., Слипенко А.К. Дидактические материалы по математике: Учебное пособие.- К.: Высшая школа.,2005
4 Валеев К.Г., Джаллатова И.А. Высшая математика: Учеб. пособие. в 2-х ч - К.:КНЭУ,2001
5 Лейфура В.М. Математика: Учебник для студентов эконом. Специальностей вуз. учеб. заведений I-II уровней аккредитации - К.: Техника, 2003
Дополнительная
6 Алгебра и начало анализа. ч II под. ред. Яковлева Г.М. – М.:наука,1987
7 Геометрия. Под. Ред. Яковлева Г.М. –М.: наука, 1988
8 Математика для техникумов. под. ред. Валуце И.И –М.: наука, 1989
Интернет-источники:
1 http://en.edu.ru - естественно - научный портал
2 http://www.bestlibrary.ru - On–line библиотека
3 http://www.km.ru/literature/ - электронная библиотека LIB.KM.ru
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к изучению учебной дисциплины «Математика»
для студентов заочного отделения
2019
СОДЕРЖАНИЕ
Тема 1. Комплексные числа…………………………………………………..3
Тема 2. Аналитическая геометрия………………..…………………………..5
Тема 3. Функция и её свойства…………………………………………………...8
Функция. Свойства функций. Графики функций…………………………...9
Преобразование графиков функций…………………………………….10
Предел функции. 1 и 2 замечательные пределы………………………..11
Непрерывность функции. Точки разрыва………………………………11
Тема 4. Дифференциальное исчисление функции одной переменной …12
Формулы дифференцирования элементарных функций……………….12
Правила дифференцирования функций………………………………….13
Производная сложной функции………………………………………….14
Общая схема исследования функций и построения их графиков……..14
Тема 5. Неопределенный интеграл. Методы интегрирования………….17
Таблица простейших интегралов………………………………………...17
Метод замены переменной (метод подстановки)……………………….18
Метод интегрирования по частям………………………………………..19
Тема 6. Определенный интеграл …………………………………….………20
Геометрические приложения определенного интеграла………………20
Тема 7. Дифференциальные уравнения …………………………..………..22
Дифференциальные уравнения первого порядка с разделяющимися переменными…………………………………………………………………….22
Однородные дифференциальные уравнения первого порядка………..23
Линейные дифференциальные уравнения первого порядка…………..25
Список рекомендуемой литературы …….………………………………...27
Тема 1. КОМПЛЕКСНЫЕ ЧИСЛА
В связи с развитием алгебры потребовалось ввести сверх прежде известных положительных и отрицательных чисел числа нового рода. Они называются комплексными.
Комплексное число имеет вид a + bi; здесь a и b – действительные числа , а i – число нового рода, называемое мнимой единицей.
“Мнимые” числа составляют частный вид комплексных чисел
(когда а = 0). С другой стороны, и действительные числа являются частным видом комплексных чисел (когда b = 0).
Действительное число a назовем абсциссой комплексного числа a + bi; действительное число b – ординатой комплексного числа
a + bi. Основное свойство числа i состоит в том, что
i 2 = -1. (1)
Действительное число а записывается также в виде a + 0 i (или a – 0 i).
П р и м е р ы. Запись 3 + 0 i обозначает то же, что запись 3. Запись –2 + 0 i означает –2.
Комплексное число вида 0 + bi называется “чисто мнимым”. Запись bi обозначает то же, что 0 + bi .
Два комплексных a + bi , a ’ + b ’ i считаются равными, если у них соответственно равны абсциссы и ординаты.
Действия над комплексными числами в алгебраической форме
О п р е д е л е н и е. Суммой комплексных чисел a + bi и a ’ + b ’ i называют комплексное число ( a + a ’) + ( b + b ’) i.
Пример 1. (-3 + 5 i ) + (4 – 8 i ) = 1 - 3 i
Два комплексных числа a+bi и a-bi называются сопряженными. Сумма сопряженных комплексных чисел равна действительному числу.
О п р е д е л е н и е. Разностью комплексных чисел a + bi (уменьшаемое) и a ’ + b ’ i (вычитаемое) называется комплексное число ( a – a ’) + ( b – b ’) i.
Пример 1. (-5 + 2i) – (3 – 5i) = -8 + 7i
Пример 2. (3 + 2i) – (-3 + 2i) = 6 + 0i = 6
О п р е д е л е н и е. Произведением комплексных чисел a + bi и a ’ + b ’ i называется комплексное число
(aa’ – bb’) + (ab’ + ba’)i.
З а м е ч а н и е . На практике нет нужды пользоваться формулой произведения. Можно перемножить данные числа, как двучлены, а затем положить, что i 2 = -1.
Пример 1. (1 – 2i)(3 + 2i) = 3 – 6i + 2i – 4i 2 = 3 – 6i + 2i + 4 = 7 – 4i.
Пример 2. (a + bi)(a – bi) = a2 + b 2
О п р е д л е н и е. Разделить комплексное число a + bi на комплексное число a’ + b’i – значит найти такое число x + yi, которое, будучи помножено на делитель, даст делимое.
Если делитель не равен нулю, то деление всегда возможно, и частное единственно. На практике частное удобнее всего находить следующим образом.
Пример 1. Найти частное (7 – 4 i ):(3 + 2i).
Записав дробь (7 – 4 i )/(3 + 2 i), расширяем её на число 3 – 2 i, сопряженное с 3 + 2 i. Получим:
((7 – 4i)(3 - 2i))/((3 + 2i)(3 – 2i)) = (13 – 26i)/13 = 1 – 2i.
Пример 1. (-2 +5i)/(-3 –4i) = ((-2 + 5i)(-3 – 4i))/((-3 – 4i)( -3 + 4i)) = (-14 –23i)/25 = -0,56 – 0.92i.
Геометрическое изображение комплексных чисел.
Комплексные числа можно изобразить на числовой плоскости прямоугольную систему координат с одним и тем же масштабом на обеих осях. Комплексное число a + bi мы изображаем точкой М, у которой абсцисса х равна абсциссе а комплексного, а ордината у равна ординате b комплексного числа.
Комплексные можно изображать также векторами, начинающимися в точке О и оканчивающимися в соответствующей точке числовой плоскости. Так, комплексное число -2 + 6 i можно изобразить не только точкой В, но также вектором ОВ ; комплексное число
–6 – 2 i изображается вектором ОС и т. д.
В 6 у у
r b
q
О х a x
6 С
Модуль и аргумент комплексного числа.
Длина вектора, изображающего комплексное число, называется модулем этого комплексного числа. Модуль всякого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа a + bi обозначается | a + bi |, а также буквой r. Из чертежа видно, что
r = | a + bi | = a 2 + b 2
Модуль действительного числа совпадает с его абсолютным значением. Сопряжённые комплексные числа a + bi u a – bi имеют один и тот же модуль.
Тригонометрическая форма комплексного числа.
Абсцисса а и ордината b комплексного числа a + bi выражаются через модуль r и аргумент q. Формулами
a = r cos q; b = r sin q.
Поэтому всякое комплексное число можно представить в виде
r(cos q + i sin q), где r > 0.
Показательная форма комплексного числа
Комплексное число так же можно представить  в виде
в виде
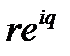
Тема 2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Основные формулы
Расстояние между двумя точками плоскости М1(x 1 , y 1) и М2(х2,у2)
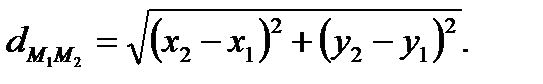 (1.1)
(1.1)
Координаты точки С, делящей отрезок АВ в отношении 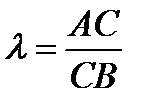
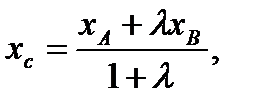
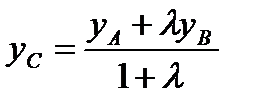 . (1.2)
. (1.2)
Если точка С является серединой отрезка АВ, то ее координаты
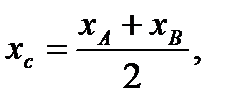
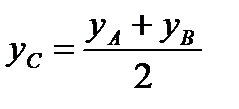 . (1.3)
. (1.3)
Уравнение прямой с угловым коэффициентом
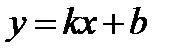 , (1.4)
, (1.4)
где 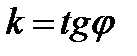 - угловой коэффициент.
- угловой коэффициент.
Уравнение прямой, проходящей через точку М1(х1 ,у1) в данном направлении
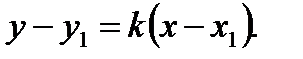 (1.5)
(1.5)
Если в уравнении (1.5) k — произвольное число, то это уравнение является уравнением пучка прямых, проходящих через точку М1( x 1 , y 1 ).
Уравнение прямой, проходящей через две точки М1(x 1 , y 1) и М2(х2,у)
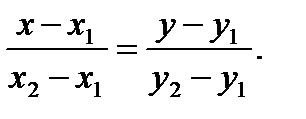 (1.6)
(1.6)
Уравнение прямой в отрезках
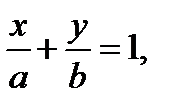 (1.7)
(1.7)
где a и b- отрезки, отсекаемые прямой на осях Ох и Оу соответственно.
Общее уравнение прямой
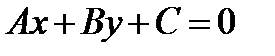 . (1.8)
. (1.8)
Угол а между двумя прямыми 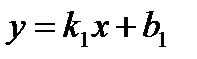 (I) и
(I) и 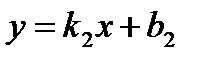 (II)
(II)
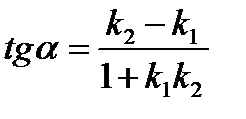 , (1.9)
, (1.9)
где стрелка означает, что угол 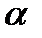 получается поворотом прямой (I)
получается поворотом прямой (I)
к прямой (II) против часовой стрелки.
Условие параллельности прямых 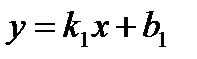 и
и 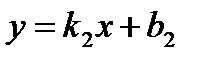
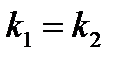 (1.10)
(1.10)
Условие перпендикулярности прямых 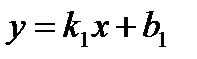 и
и 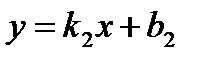
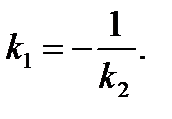 (1.11)
(1.11)
Расстояние от точки Мо (хо,уо) до прямой Ах + By + С=0
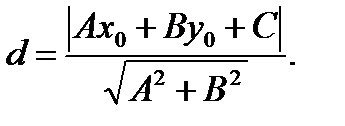 (1.12)
(1.12)
Координаты точки пересечения двух прямых находятся путем решения системы уравнений этих прямых.
Задание 1
Дата: 2019-11-01, просмотров: 325.