Задача №1:

В научной лаборатории имеется 350 подопытных мышей, причём 35% всех мышей – белые, 15% – серые и остальные мыши чёрного цвета. Вероятность того, что новый состав не подействует на мышь белого цвета, составляет 10%, на мышь серого цвета – 30% и на мышь чёрного цвета – 22%. Какова вероятность того, что на случайно выбранную мышь состав не подействует?

Решение:

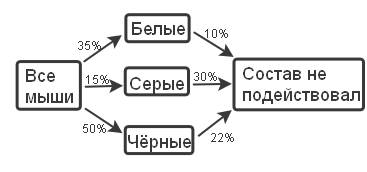Если А – «состав не подействовал», В1 – «мышь белая», В2 – «мышь серая» и В3 – «мышь чёрная» то Р(В1) = 0.35, Р(В2) = 0.15 и Р(В3) = 0.5;
Р(A/В1) = 0.35*0.1 = 0.035, Р(A/В2) = 0.15*0.3 = 0.045 и
Р(A/В3) = 0.5*0.22 = 0.11

Р(А) = 0.035+0.045+0.11 = 0.19 = 19%

Задача №2:

В приюте для животных находятся 150 кошек рыжего цвета, 90 кошек белого цвета и 110 чёрных кошек. Среди рыжих кошек 35% котов, среди белых – 40%, среди чёрных – 1%. Какова вероятность получить кота?

Решение:

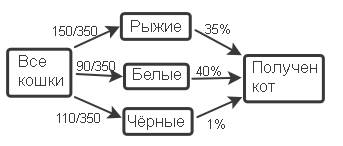Перед тем, как найти вероятность получения кота из всех кошек, необходимо найти, какую часть кошки каждого цвета составляют от всех кошек. Для рыжих – 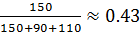, для кошек белого цвета –  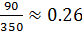и для чёрных кошек – 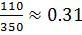. Теперь можно найти вероятность получения кота:

Р(А) = 0.43*0.35 + 0.26*0.4 + 0.31*0.01 = 0,1505+ 0,104+ 0,0031 = 0,2576

Задача №3:

Имеются три ящика с шарами. В одном из них 4 белых и 5 чёрных шаров, во втором – 5 белых и 4 чёрных, а в третьем – 6 белых. Наугад выбран один ящик и из него вынут шар. Найти вероятность того, что шар окажется белым.

Решение:

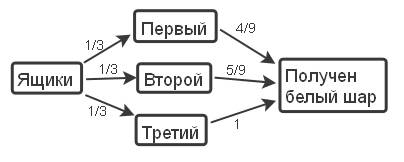Из условия находим, что вероятность вытащить белый шар из первого ящика равен , из второго – , а в третьем только белые шары, следовательно, вероятность вытащить белый шар равна 1. Далее по формуле полной вероятности вычисляем вероятность получения белого шара из наугад взятого ящика: +  +  = .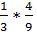

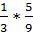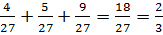Задачи для решения через формулу Байеса.

Задача №1:

Три декоратора завязывают банты на стульях. У первого декоратора вероятность того, что бант развяжется, равна 0.5, у второго – 0.2, а у третьего 0.1. Первый декоратор завязал 60 бантов, второй – 80, третий – 90. Во время праздника один из бантов развязался. Какова вероятность того, что этот бант был завязан вторым декоратором?

Решение:

Для начала вычислим процентное соотношение всех завязанных бантов. 60+80+90 = 230 бантов всего было завязано. Первый декоратор завязал 0.26 (т.е. 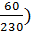всех бантов, второй – 0.35, а третий – 0.39.

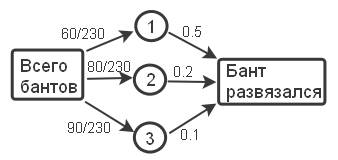Теперь найдём вероятность события А – «бант развязался». Для этого воспользуемся формулой полной вероятности и получим: 0.5*0.26 + 0.2*0.35 + 0.1*0.39 = 0.13+0.07+0.039 = 0.239

Зная эту вероятность, мы можем найти вероятность того, что развязанный бант был завязан вторым декоратором, используя формулу Байеса:

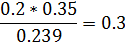
Задача №2:

Имеются три ящика с шарами. В одном из них 4 белых и 5 чёрных шаров, во втором – 5 белых и 4 чёрных, а в третьем – 6 белых. Наугад выбран один ящик и из него вынут шар. Найти вероятность того, что белый шар был вынут из второго ящика.

Решение:

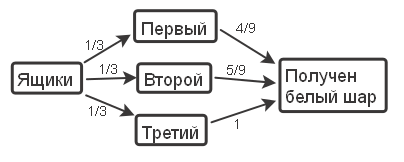Имея значение полной вероятности равное , очень легко вычислить вероятность того, что белый шар извлечён именно из второго ящика. .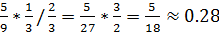

ЗАКЛЮЧЕНИЕ

В рамках данной работы:

•   рассмотрены три подхода к решению вероятностных задач

•   подробно рассмотрена формула условной вероятности

•   выведена формула полной вероятности и выведена формула Байеса как следствие ФПВ

•   решены и проиллюстрированы некоторые примеры вероятностных задач

Изучение основ теории вероятностей включено в курс математики для средней школы. Задачи на безусловную или условную вероятность включены в единый государственный экзамен по математике.  

Изучение теории вероятностей в школе – это признание обществом необходимости формирования современного мировоззрения. Это связано с  тем, что вероятностные закономерности универсальны: физика, химия, биология, математика, весь комплекс социально-экономических наук развивается на базе вероятностно-комбинаторной математики.

Простые задачи на безусловную вероятность обычно решать очень легко, и все решение сводится к некой комбинаторной задаче. Решать же задачи на нахождение полной или условной вероятности немного сложнее. В таких ситуациях очень помогает составление графа вероятностей (или дерева) или обыкновенной простой наглядной схемы.

Навык составления иллюстраций крайне важен при решении сложных нетривиальных задач. Иллюстрации могут быть полезны экономистам и маркетологам для презентации новых путей расширения бизнеса/товарооборота (как в задаче №1 из пункта 3.1).

Обучение детей в школе составлению деревьев вероятностей поможет им не только решить ту или иную задачу, но и развить свои творческие способности. Сложные для понимания задачи становятся гораздо проще для восприятия, если к ним имеется иллюстрация.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ:

Ø А.Н.Колмогоров «Введение в теорию вероятностей» / А.Н.Колмогоров, И.Г.Журбенко, А.В.Прохоров – М: Наука. Главная редакция физико-математической литературы, 1982, 160 с. – (Библиотечка «Квант». Вып. 23)

Ø https://ru.wikipedia.org – формулировка основных понятий

Ø http://mathematichka.ru/ege/problems/problem_B10P1.html - задачи на нахождение вероятности.

Ø http://www.mathprofi.ru/files/gotovye_zadachi_na_fpv_i_formuly_bajesa.pdf - формулировки задач на полную вероятность.