Задача №1:

На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.

Решение:

Удобными являются 12+18, т.е. 30 мест. Таким образом, P(A) =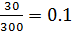

Пояснение:

Так как один человек способен занять только одно место, события независимы. А так как в условии специально оговорено, что при регистрации место выбиралось случайно, то и равновозможны. Поэтому, фактически, мы считали не события, а места в самолёте.

Задача №2:

В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.

Решение:

Вычислим количество рейсов – 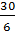 = 5. Турист П. может полететь любым из них, но нас интересует только один рейс – первый. Таким образом вероятность полететь первый рейсом равна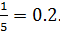

Пояснение:

В этой задаче элементарным событием является сформированный рейс вертолёта. Один человек может попасть только на один рейс, т.е. только в одну группу из 6-ти человек, - события независимы. По условию задачи порядок рейсов случаен, т.е. все рейсы для каждой группы равновозможны. Считаем рейсы и находим вероятность.

Задача №3:

Из множества трёхзначных натуральных чисел наугад выбрали число. Какова вероятность того, что оно делится на 4?

Решение:

Решение данной задачи состоит из двух этапов. Для начала нам необходимо узнать, сколько чисел вообще есть в промежутке от 100 до 999 и сколько из них делятся на 4. Если числовой промежуток небольшой, то числа можно найти перебором, выписав их на бумагу. В нашем случае этот способ слишком трудозатратный, поэтому поступим немного по-другому. Всего наш промежуток содержит 999–100 чисел, т.е. 899. Они составляют 224 полные группы и 1неполную ( 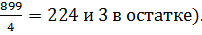 В каждой полной группе есть ровно одно число, которое делится на 4. В последней группе три числа: 997, 998 и 999 и ни одно из них не делится на 4. Итого, мы имеет 224 подходящих числа. Вторым этапом будет непосредственно нахождение вероятности: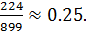

Задача №4:

Известно, что курс евро к рублю может возрасти с вероятностью 0.55, а курс доллара к рублю может возрасти с вероятностью 0.35. Вероятность того, что возрастут оба курса, равна 0.3. Найти вероятность того, что курс евро или доллара по отношению к рублю возрастёт.

Решение:

Событие А – возрастёт курс евро, событие B – возрастёт курс доллара. Тогда, P(A) = 0.55, P(B) = 0.35, P(A∩B) = 0.3. Следовательно, по аксиоме 4 верно следующее равенство:

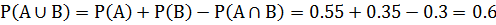
Выводы главы 1 .

Не смотря на удобство различных подходов к решению вероятностных задач, ни один из них не дают исчерпывающего определения реального содержания понятия вероятность. Предположение о том, что при неких условиях для благоприятного события существует определённая вероятность, является гипотезой, которая в каждой задаче требует проверки и обоснования.

По численным значениям вероятностей, определённых при классическом и статистическом подходе можно вычислить новые вероятности.

Решение вопроса о практической достоверности непосредственно связано с вопросом о том, какими вероятностями можно пренебрегать на практике. Он решается для каждой задачи по-разному и уже за рамками теории вероятностей. Например, в каком-то случае пренебрегают вероятностью 0.05: если условия практической задачи допускают такую долю ошибок (в среднем 5 случаем на 100 экспериментов), то мы считаем достоверным событие, которое происходит с вероятностью 0.95. В других случаях принято пренебрегать лишь вероятностями 0.001, а иногда требуется еще большее приближение вероятности отсутствия ошибки.

В следующей главе мы более подробно ознакомимся с термином вероятность, узнаем, что такое условная вероятность, независимость событий и выведем формулу полной вероятности.