Новые понятия теории вероятностей.
Для дальнейшего изучения теории вероятностей, нам необходимо ввести некоторые новые термины.
Сумма (объединение) событий А и В – это событие, состоящее как из исходов составляющих А, так и из исходов, составляющих В. Исходы, входящие и в А и в В учитываются только один раз. Сумма обозначается символом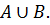 
Сумма может состоять из любого числа событий. Множество
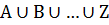состоит из тех исходов, которые входят в состав хотя бы одного из событий A, B, … , Z.
Пересечение событий А и В – это событие, состоящее только из тех исходов, которые входят как в А, так и в В. Пересечение обозначается символом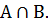 
Пересечение так же может состоять из любого числа событий. Множество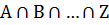 
состоит из тех исходов, которые входят в состав каждого из событий A, B, … , Z.
Противоположное к А событие (дополнение А) – это событие, которое состоит из всех исходов, не входящих в А. Дополнение обозначается символом Ᾱ.
Для лучшего понимания и запоминания (особенно для школьников) часто бывает полезна графическая иллюстрация данных понятий. На рисунке каждая точка обозначает некий исход события. Само событие – это заштрихованная область с точками, окружёнными рамкой.
Для приведённого ниже рисунка общее число исходов равно 36. Считаем число точек в каждой области и получаем:
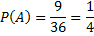
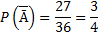
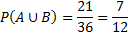
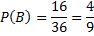
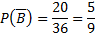
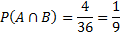
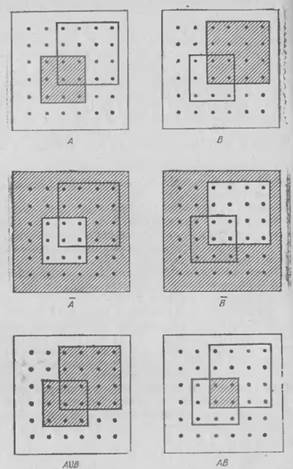Говорят, что событие А влечет за собой событие В, если все исходы, составляющие А, входят и в В. Обозначается символом 
.
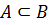Невозможное событие будем обозначать символом V. Это такое событие, в которое не входит и один из исходов.
Условная вероятность.
При решении вероятностных задач часто важно определить вероятность наступления какого-либо события, когда о нём имеются дополнительные сведения. Обычно нужно найти вероятность события А, при условии, что некоторое событие В уже произошло. Например, на экскурсии всех людей поделили на 5 групп. Изначально ваш шанс попасть в первую группу равен 20%, но после того, как экскурсовод сказал, что вы не попали ни в пятую, ни в третью группу, вероятность оказаться в первой группе возросла и стала равна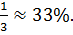 
Условная вероятность события А при условии, что наступило событие В – это отношение благоприятствующих А исходов, которые так же благоприятствуют В к числу всех исходов, которые благоприятствуют В. Обозначать условную вероятность будем символом P(A/B). Если В – невозможное событие, то P(A/B) будем считать равной нулю.
Если событию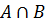 
благоприятствуют k исходов, то 
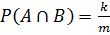. В таком случае:
P(A/B) =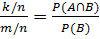 
Данное равенство очень важно для нас. Оно позволяет вычислять условную вероятность события А, используя безусловные вероятности
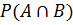и 
.
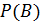Пример №1:
Три нужных вам книги находятся на одной из 15 стеллажей с 10 полками на каждом. Вы точно не знаете, где именно лежат книги, но вам точно известно, что первая лежит на стеллаже, номер которого делится на 5; вторая лежит на стеллаже, номер которого делится на 3, на полке, номер которой делится на 4; сумма номеров полки и стеллажа третьей книги равна 17. В каком случае вероятность попасть на нужную вам полку с первого раза наибольшая?
Решение:
Пусть А – «номер полки делится на 5». Очевидно, что число благоприятствующих для А исходов = 15*2 = 30.
Пусть В – «номер стеллажа делится на 3, а номер полки делится на 4». Число благоприятствующих исходов для В = 5*2 = 10.
Пусть С – «сумма номеров полки и стеллажа равен 17». Количество благоприятствующих исходов для этого события равно 9.
Наконец D – это событие, при котором мы с первого раза попадём на нужную нам полку. При таком раскладе вероятности таковы:
P(D/A) =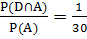 
, P(D/B) = 
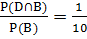, P(D/C) = 
.
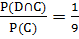Для сравнения вычислим безусловную вероятность события D:
P(D) =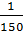 
Основные свойства условной вероятности:
1. 0 ≤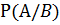 
≤ 1, при чём если AB – невозможное событие, то 
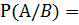0 и если В⊂А, то 
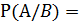1;
2. Если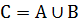 
и АВ = V, то для любого события D справедливо 
.
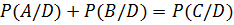3. Теорема сложения вероятностей распространяется на случай, когда А =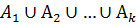 
, 
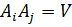при i ≠ j, i, j = 1, 2, … , k.
.
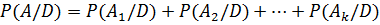4. Если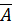 
– событие противоположное 
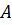, то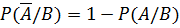 
.
Пример №2:
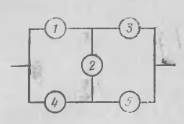Известно, что цепь проводит ток. Какова вероятность того, что элемент 1 проводит ток? Какова вероятность, что элемент 2 проводит ток? Какая из этих вероятностей выше?
Решение:
Пусть А – это событие при котором элемент 1 проводит ток, В – событие при котором элемент 2 проводит ток и С – событие при котором вся цепь проводит ток. Так как каждый элемент цепи может иметь только два состояния, то всего различных комбинаций этих состояний 32. В данном случае методом перебора можно легко определить, в каких случаях цепь будет проводить ток.
Всего получаем 16 вариантов, в которых цепь проводит ток. То есть P(C) = 0.5.
Далее находим P(A/C) =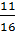 
, P(B/C) = 
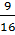. Таким образом вероятность наступления события А выше, чем В.
Независимость событий.
В теории вероятностей и ее применении играет очень важную роль понятие независимости двух событий. Событие А называется независимым от события В, если имеет место равенство P(A/В) = Р(А). То есть событие А независимо от В, если условная вероятность события А при условии, что событие В произошло, совпадает с условной вероятностью события А.
Например, из колоды вынимают оду карту наугад. Какова вероятность того, что эта карта окажется шестёркой? Т.к. всего в колоде 36 карт, очевидно, что эта вероятность равна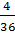 
или 
. После этого нам сказали, что вынутая карта является красной. Изменилась ли вероятность достать шестёрку? На данный момент она будет составлять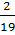 
, то есть . Мы видим, что вероятность не изменилась, следовательно событие А не зависит от В.
Если два события А и В независимы друг от друга, то для них возможно применить теорему о умножении вероятностей, которая имеет вид:
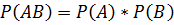
Если события А и В произвольны, то данная теорема примет вид:
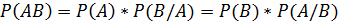
Далее мы перейдём к выводу важной формулы, которая называется формула полной вероятности.
Формула полной вероятности.
Следствием основных теорем – теоремы сложения вероятностей и теоремы умножения вероятностей – является так называемая формула полной вероятности.
Пусть для некоторых событий А,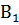 
, 
, … , 
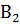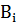нам известны вероятности наступления событий 
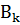и условная вероятность наступления события А, при условии наступления события из множества { 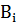}. Так же известно, что
А⊂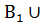 
… 
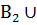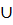
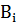, при чём события 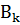попарно несовместны. Можем ли мы, опираясь только на эти данные, найти вероятность наступления события А? С использованием формулы полной вероятности, ответ да, можем.
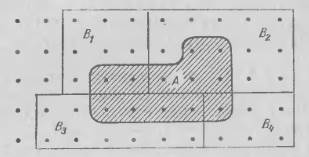Данное изображение наглядно иллюстрирует нам, что имеет место быть следующая формула: 
.
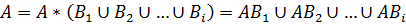Из несовместности событий 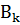вытекает и несовместность событий 
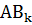. Следовательно, мы можем воспользоваться теоремой сложения вероятностей:
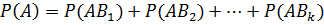
Но так как при любом k (1 ≤ k ≤ i) справедливо
,
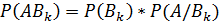то
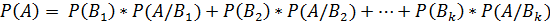
Это и есть формула полной вероятности. Теперь мы легко сможем решать задачи, используя эту формулу.
Пример №1:
Партия фруктов содержит 25% фруктов, выращенных фермой 1, 40% - фермой 2 и оставшиеся 35% - фермой 3. Для фермы 1 вероятность получить кислый фрукт равна 0.07, для фермы 2 – 0.1, для фермы 3 – 0.045. Какова вероятность, что выбранный наугад фрукт окажется кислым?
Решение:
Пусть А – «фрукт кислый»,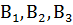 
- фрукт выращен соответственно фермой 1, 2, 3. По условиям задачи имеем 
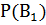= 0.25, 
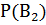= 0.4, 
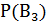= 0.35, 
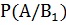= 0.07, 
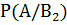= 0.1 и 
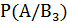= 0.045. По формуле полной вероятности вычисляем, что
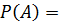0.25*0.07 + 0.4*0.1 + 0.35*0.045 = 0.0175 + 0.04 + 0.01575 = 0.07325.
Теорема Байеса.
Теорема Байеса названа в честь её автора Томаса Байеса (1702—1761) — английского математика и священника, который первым предложил использование теоремы для корректировки убеждений, основываясь на обновлённых данных.
Данная теорема позволяет определить вероятность какого-либо события при условии, что произошло другое статистически взаимозависимое с ним событие. Другими словами, по формуле Байеса можно более точно пересчитать вероятность, взяв в расчет как ранее известную информацию, так и данные новых наблюдений.
Теорема Байеса является простым следствием из формулы полной вероятности, и формулируется следующим образом:
Пусть события Bi попарно несовместны и A ⊂ B 1 B 2 … Bk , тогда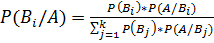 
.
Эту же формулу можно вывести из формул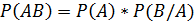 
и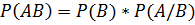 
. Из них следует формула 
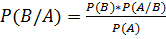, где
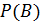· - априорная вероятность гипотезы B,
· 
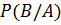– апостериорная вероятность гипотезы А при наступлении события В,
· 
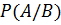- вероятность наступления события В при истинности гипотезы А,
· 
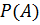- полная вероятность наступления события B.
Так как 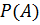выводится из формулы полной вероятности, то мы можем заменить 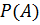на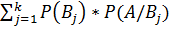 
в формуле Байеса и т.о. получаем
.
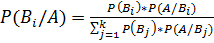где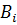 
- проверяемая нами причина.
Гипотезы – это предполагаемые причины, которые могли повлечь за собой данное событие.
Априорная вероятность – это безусловная вероятность справедливости гипотезы. Т.е. априорная вероятность вычисляет, насколько вероятна та или иная причина вообще.
Апостериорная вероятность – это условная вероятность появления причины с учётом полученных данных о событии, которое эта причина повлекла.
«Физический смысл» теоремы Байеса заключается в том, что она позволяет вычислить по известному факту события вероятность того, что оно было вызвано данной причиной.
Имея данную формулу, попробуем решить задачу, обратную задаче 1.
Пример №1:
Пусть выполняются условия из задачи №1. Наугад выбранный фрукт оказался кислым. Чему равна вероятность, что он был выращен на ферме 1, 2, 3?
Решение:
В данной задаче нам необходимо найти вероятност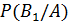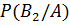и 
, 
и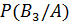 
.
= 
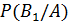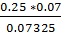≈ 0.24, = 
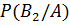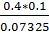≈ 0.55, = 
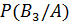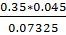≈ 0.21.
Таким образом, вероятность, что кислый фрукт был выращен фермой 2 чуть больше, чем в два раза больше, чем первой или третьей фермой.
Выводы главы 2
В данной главе мы разобрали понятие условной вероятности, независимости событий друг от друга и вывели формулу полной вероятности. Так же мы полностью разобрали и решили несколько задач по этим темам.
Как уже было сказано выше, условная вероятность позволяет более точно определить вероятность наступления/не наступления того или иного интересующего нас события. Порой разница между значением, полученным при использовании формулы условной вероятности и значением, полученным при использовании формул безусловной вероятности, огромна.
Формулы нахождения безусловной вероятности очень удобны для изучения в школе. Они достаточно просты и помогают школьникам понять, что же такое вероятность наступления события и как её вычислить. Формулы условной вероятности можно дать для изучения в старших классах, для более углубленного изучения теории вероятностей.
Формула же полной вероятности может оказаться для школьников слишком сложной, но её можно оставить им на самостоятельное поверхностное изучение, исключительно для развития их мышления и кругозора.
Формула Байеса поможет определить вероятность того или иного события, которое привело к известному исходу.
В третьей заключительной главе этой работы будут представлены задачи на условную вероятность, их графические иллюстрации и полный разбор.
Дата: 2019-11-01, просмотров: 199.
