Классический подход состоит в том, что вероятность какого-либо благоприятного исхода равна отношению числа благоприятных исходов к общему числу равновозможных исходов. Вычисление вероятностей при этом сводится к подсчёту элементов того или иного множества и оказывается чисто комбинаторной задачей. Классическое определение можно использовать тогда, когда мы имеем возможность «предсказать» вероятность, т.е. при условии т.н. равновозможности всех результатов.

Равновозможность – это объективное свойство испытаний, определяемое условиями их проведения, и устанавливаемое с некоторой известной степенью точности.

Для какого-либо случайного события А частота его наступления равна , где m – число испытаний, в которых А наступило, а n – достаточно большое количество всех проведённых испытаний. Наличие у события А вероятности наступления равной p, проявляется в том, что в каждой, достаточно длинной серии испытаний, частота А будет приблизительно равна p.

В качестве примера можно рассматривать опыт с подбрасыванием монеты. При достаточно большой высоте подбрасывания, вероятность выпадения орла = 50%. В таблице приведены результаты данного опыта, проведенного в разное время разными людьми.

	n
Бюффон	4040	0.507
Де Морган	4092	0.5005
Джевонс	20480	0.5068
Романовский	80640	0.4923
Пирсон К.	24000	0.5005
Феллер	10000	0.4979

Данные этой таблицы наглядно показывают, что вероятность действительно приблизительно равна 0.5 или же 50%. Этот результат кажется вполне удовлетворительным, но если применить специальные вероятностные методы, то можно будет сделать вывод, что вероятность на самом деле другая. Это явление будет следствием того факта, что монета никогда не бывает идеально симметричной. И, тем не менее, подобная модель с k равновозможными исходами позволяет достаточно точно описать различные случайные явления и потому не может быть отвергнута.

Численное значение вероятностей при Броуновском движении и движении по прямой получается из классического определения.

Для Броуновского движения число возможных вариантов пути частицы от начальной точки равно 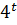, где t – число шагов, совершённых этой частицей.

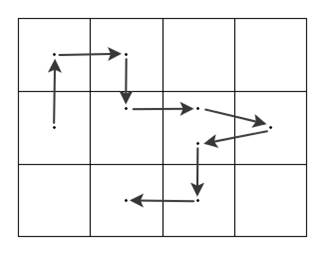
На рисунке изображён возможный путь частицы за 8 шагов.

Если предположить, что частица движется по поверхности, расчерченной на квадратики, и всегда помещается в центре занимаемого квадратика, то за t шагов она сможет удалиться от начального значения не более чем на расстояние t*h, где h – длина стороны квадратика. Для t = 5 она отдалится на максимально расстояние только в 4 случаях из 1024! В 400 случаях это расстояние будет равно h, еще в 400 – 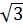. И лишь в оставшихся 20% частица уйдёт дальше.

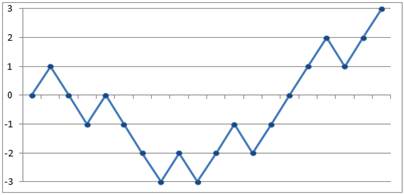Рассмотрим еще более простую задачу блуждания по прямой. За один шаг частица продвинется на расстояние h вверх или вниз. На горизонтальной оси удобно откладывать число шагов. На графике изображён возможный вариант движения частицы. Легко понять, что в этой задаче число всех возможных способов перемещения частицы за t шагов равно .

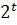Блуждание такого рода осуществляется в специальном приборе, который называется доской Гальтона.