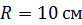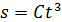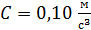101. Материальная точка движется по окружности радиусом . Зависимость пути от времени задана уравнением , где . Определите нормальное  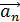и тангенциальное  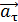ускорение точки в момент времени, когда линейная скорость точки  .

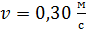  102. Колесо радиусом 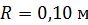 вращается так, что зависимость угла поворота колеса от времени дается уравнением 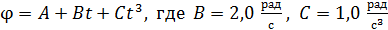. В момент времени  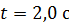после начала движения для точек на ободе колеса определите: 1) угловую скорость 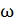; 2) угловое ускорение 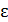; 3) нормальное  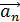и тангенциальное  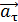ускорение.

  103. Материальная точка движется по окружности радиусом 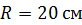. Зависимость пути от времени задана уравнением 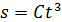, где 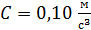. Определите нормальное  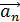и тангенциальное  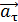ускорение точки в момент времени, когда линейная скорость точки .

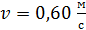  104. Диск радиусом 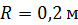 вращается так, что зависимость угла поворота диска от времени дается уравнением 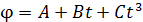, где 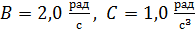. В момент времени  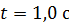после начала движения для точек на ободе колеса определите: 1) угловую скорость 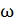; 2) угловое ускорение 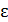; 3) нормальное  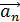и тангенциальное  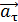ускорение.

  105. Материальная точка движется по окружности радиусом 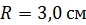. Зависимость пути от времени задана уравнением 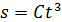, где 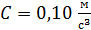. Определите нормальное  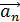и тангенциальное  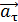ускорение точки в момент времени, когда линейная скорость точки  .

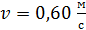  106. Колесо радиусом 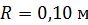 вращается так, что зависимость угла поворота колеса от времени дается уравнением 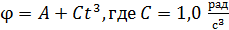. В момент времени  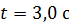после начала движения для точек на ободе колеса определите: 1) угловую скорость 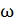; 2) угловое ускорение 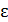; 3) нормальное  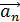и тангенциальное  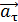ускорение.  

  107. Материальная точка движется по окружности радиусом 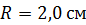. Зависимость пути от времени задана уравнением 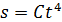, где 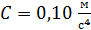. Определите нормальное  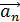и тангенциальное  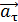ускорение точки в момент времени, когда линейная скорость точки .

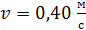  108. Диск радиусом 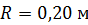 вращается так, что зависимость угла поворота диска от времени дается уравнением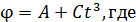 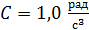. В момент времени  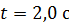после начала движения для точек на ободе колеса определите: 1) угловую скорость 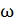; 2) угловое ускорение 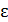; 3) нормальное  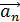и тангенциальное  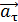ускорение.

  109. Материальная точка движется по окружности радиусом 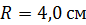. Зависимость пути от времени задана уравнением 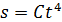, где 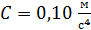. Определите нормальное  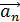и тангенциальное  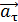ускорение точки в момент времени, когда линейная скорость точки  .

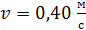  110. Колесо радиусом 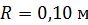 вращается так, что зависимость угла поворота колеса от времени дается уравнением 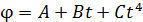, где 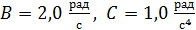. В момент времени  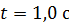после начала движения для точек на ободе колеса определите: 1) угловую скорость 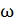; 2) угловое ускорение 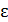; 3) нормальное  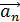и тангенциальное  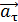ускорение.

  Закон сохранения момента импульса (ЗСМИ)

   111. Горизонтальная платформа массой 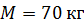 и радиусом  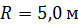вращается свободно относительно вертикальной оси с частотой 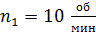. Человек массой  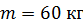стоит на краю платформы. С какой частотой  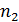будет вращаться платформа, если человек перейдет от края платформы к ее центру? Какую работу  совершит человек при переходе? Момент инерции платформы рассчитайте, как диска, а человека – как материальной точки.

  112. Диск радиусом 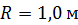 и массой  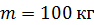вращается с частотой 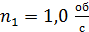. В центре диска стоит человек и держит гири в вытянутых в стороны руках. Определите угловую скорость  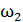вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от величины  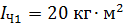до 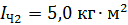. Какую работу  совершит человек?

  113. Платформа (диск) радиусом 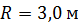 и массой  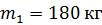может вращаться без трения вокруг вертикальной оси. С какой угловой скоростью  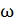будет вращаться платформа, если по ее краю пойдет человек массой 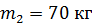со скоростью 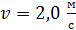относительно платформы?

  114. На краю платформы (диска) радиусом 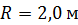, которая вращается свободно относительно вертикальной оси с частотой 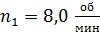, стоит человек массой 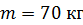. Когда человек перешел в центр платформы, она стала вращаться с частотой 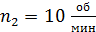. Определите массу  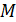платформы. Момент инерции человека рассчитайте, как для материальной точки.

  115. На неподвижной скамье Жуковского стоит человек и ловит рукой мяч массой 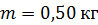, который летит горизонтально со скоростью 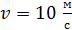. С какой угловой скоростью  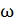будет вращаться скамья с человеком, поймавшим мяч? Расстояние мяча от оси вращения скамьи 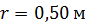. Момент инерции скамьи с человеком .

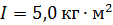  116. Человек стоит в центре скамьи Жуковского и держит в руках стержень, расположенный вертикально вдоль оси вращения скамьи. Скамья с человеком вращается с угловой скоростью 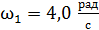. С какой угловой скоростью  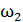будет вращаться скамья с человеком, если он расположит стержень горизонтально так, что его центр масс будет на оси скамьи. Момент инерции скамьи с человеком 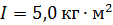. Длина стержня 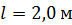, его масса .

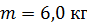  117. Человек массой 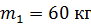 стоит на неподвижной платформе в виде диска радиусом  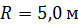и массой 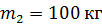. Сколько оборотов в минуту  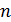будет делать платформа, если человек пойдет по окружности радиусом  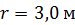со скоростью  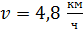относительно платформы. Момент инерции человека рассчитайте, как для материальной точки.

  118. Диск радиусом 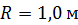 и массой  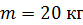вращается с угловой скоростью 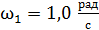. В центре диска стоит человек и держит в вытянутых в стороны руках гири массой  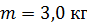каждая; расстояние гирь от оси вращения  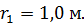Определите угловую скорость  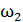вращения платформы, если человек, опустив руки, уменьшит расстояние гирь от оси до 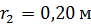. Момент инерции человека относительно оси вращения 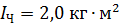. Какую работу  совершит человек?

  119. Человек стоит на неподвижной скамье Жуковского и держит  стержень, расположенный вертикально вдоль оси вращения скамьи. На конце стержня вращается колесо с частотой 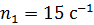. Определите угловую скорость вращения скамьи 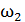, когда человек повернет стержень с колесом на угол 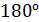. Суммарный момент инерции скамьи с человеком 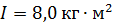. Радиус колеса 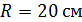, а его масса  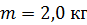равномерно распределена по ободу.

  120. Платформа в виде диска радиусом 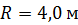 и массой  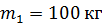может вращаться без трения вокруг вертикальной оси. С какой угловой скоростью  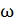будет вращаться платформа, если по ее краю пойдет человек массой  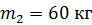со скоростью  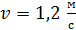относительно платформы?