93. При измерении мультиметром постоянного напряжения в диапазоне до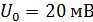 
сопротивление прибора 
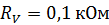. Какие сопротивления 
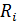используются в приборе и как они подключаются к сопротивлению 
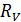, чтобы переключать диапазон измерений прибора на напряжения 
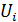, равные 2 В и 600 В?
94. При измерении мультиметром постоянного тока в диапазоне до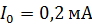 
сопротивление прибора 
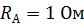. Какие сопротивления 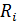используются в приборе и как они подключаются к сопротивлению 
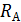, чтобы переключать диапазон измерений прибора на токи 
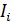, равные 200 мА и 10 А?
95. Батарея с ЭДС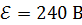 
и внутренним сопротивлением 
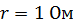замкнута на внешнее сопротивление 
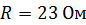. Определите полную мощность источника тока 
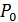, полезную мощность 
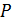и КПД батареи 
.
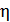96. Нагреватель электрического чайника имеет две секции. При включении одной из них вода в чайнике закипает за время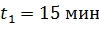 
, а при включении другой секции – через 
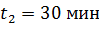. За какой промежуток времени 
закипит вода в чайнике, если соединить обе секции: а) последовательно, б) параллельно?
97. ЭДС батареи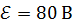 
, ее внутреннее сопротивление 
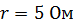. Внешняя цепь потребляет мощность 
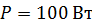. Определите силу тока в цепи, напряжение, под которым находится внешняя цепь, и ее сопротивление.
98. Генератор постоянного тока развивает ЭДС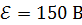 
. Ток в цепи 
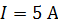. Внутреннее сопротивление источника тока 
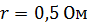. Определите мощность 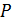, передаваемую потребителю, КПД 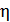и ток короткого замыкания 
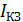источника тока, если ток подводится к потребителю по двухпроводной линии длиной 
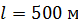. Провод линии алюминиевый, его сечение 
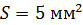, температура проводов 
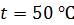. Удельное сопротивление алюминия при температуре 
: 
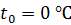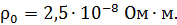
99. Определите мощность 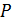, которая выделяется во внешней цепи, состоящей из двух резисторов, сопротивлением 
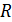каждый, если на резисторах выделяется одинаковая мощность 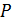, как при последовательном, так и при параллельном соединении. ЭДС источника тока 
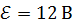, его внутреннее сопротивление 
.
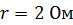100. Источник тока замыкают сначала на внешнее сопротивление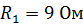 
, а затем на внешнее сопротивление 
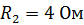. В обоих случаях за равное время 
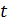на каждом сопротивлении выделяется одинаковое количество теплоты 
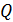. Определите внутреннее сопротивление 
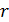источника тока.
Установочные лекции
Таблица 2
| Номер лекции | Тема занятия | Программные вопросы |
| 1 | Кинематика поступательного и вращательного движения | 1 – 5 |
| 1, 2 | Динамика поступательного и вращательного движения | 6 – 11 |
| 2, 3 | Работа. Энергия. Законы сохранения | 12–17 |
| 3 | Молекулярная физика. Явление переноса | 27, 30–33 |
| 4 | Термодинамика. I и II начала термодинамики. Энтропия. Циклы | 34– 44 |
| 5 | Электрическое поле – напряженность и потенциал. Теорема Остроградского – Гаусса. Работа сил электрического поля | 48–52 |
| 5 | Проводники и диэлектрики в электрическом поле. Электроемкость. Энергия электрического поля | 53–60 |
| 6 | Постоянный электрический ток | 61–65 |
1. 4 . Самостоятельная работа студентов
В самостоятельную работу студентов (СРС) включается следующее:
1) выполнение контрольной работы №1;
2) подготовка к выполнению лабораторных работ (см. раздел 3);
3) подготовка к экзамену (по программным вопросам и задачам);
4) изучение по рекомендуемой литературе тем, представленных в табл. 3.
Таблица 3
| Номер темы | Тема | Программные вопросы |
| 1 | Неинерциальные системы отсчета | 18–19 |
| 2 | Механические колебания | 20–24 |
| 3 | Специальная теория относительности | 25–26 |
| 4 | Распределение молекул по скоростям и в потенциальном силовом поле | 28–29 |
| 5 | Реальный газ | 45–46 |
1.5.Требования к оформлению решения задач контрольной работы
1. Приводите в своей тетради полный текст задачи, а затем краткое условие задачи, выписывая заданные и определяемые величины в общепринятых обозначениях.
2. Внимательно отнеситесь к каждому слову в формулировке задачи, чтобы выделить в ней все, в том числе и неявно заданные величины. Например: «…Найти путь, пройденный телом до остановки». Здесь неявно задана конечная скорость, равная нулю. Или в задаче говорится о газе, находящемся при нормальных условиях. Это означает, что заданы давление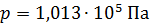 
и температура 
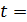0 
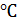, или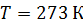 
, и т. д.
3. В решении задачи приводите рисунок, график или схему.
4. Решение задачи сопровождайте краткими, но исчерпывающими пояснениями: а) называйте используемый для решения закон, б) приводите его словесную или математическую формулировку в общем виде, в) объясняйте правомерность применения закона, уточняя формулу закона в условиях данной задачи, г) называйте величины, входящие в формулы, в том числе физические постоянные.
5. Каждую задачу стремитесь решать в общем виде, не делая промежуточных вычислений; решение задачи завершайте расчетной формулой определяемой величины.
6. Вычисляя, в расчетную формулу обязательно подставляйте значения данных и табличных величин, в единицах системы СИ.
Рекомендации к решению физических задач
1. Текст задачи следует внимательно прочитать, чтобы выяснить, какое движение (поступательное, вращательное, качение) или физическое явление рассматривается в задаче. Полезно сделать схематический чертеж или рисунок.
2. На сайте ЗИЭФ (по адресу http://zief.susu.ac.ru.), в разделе 1 – «Теоретическая часть» изучите сведения о явлении, рассматриваемом в задаче: ознакомьтесь с основными формулами и величинами. Выясните, нельзя ли применить законы сохранения (ЗСИ, ЗСМИ, ЗСМЭ) – для этого проверьте, выполняются ли в задаче условия применения закона сохранения (замкнутость механической системы, консервативность сил). Выпишите законы и формулы, которые можно использовать при решении данной задачи.
3. Запишите краткое условие задачи, выбирая для обозначения заданных и искомых величин символы, которые использованы в формулах.
4. Задачу следует решать, как правило, в общем виде, т. е. получить расчетную формулу определяемой величины, содержащую символы заданных величин и физических постоянных.
5. Вычисление определяемой величины начинайте с подстановки в расчетную формулу значений величин. При этом следует помнить, что большинство физических величин имеют свои единицы измерения. Полезно записывать их при подстановке в формулу, чтобы убедиться, что все величины взяты в единицах СИ. Только при вычислении отношений, например,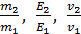 
и т. п. можно подставлять величины в любых, но одинаковых единицах, т. е. не обязательно в СИ. Если определяемых величин несколько, то вывод расчетной формулы для следующей начинайте, закончив вычисление предыдущей определяемой величины.
6. Полезно выполнять проверку расчетной формулы на совпадение единиц измерения левой и правой части равенства. Несовпадение единиц указывает на ошибку в расчетной формуле.
7. Вычисления и запись результата делайте с точностью до двух или трех (не более) значащих цифр. Незначащие нули записывайте в виде сомножителя 
. При этом, если показатель степени n соответствует приставке, то используйте её: например,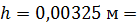 
; 
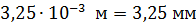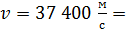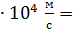3,74 
37,4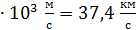 
.
Примечание: значащими цифрами числа являются все его цифры, кроме нулей, стоящих перед первой, не равной нулю цифрой (значащие цифры могут располагаться как перед, так и после запятой). Приведем примеры чисел, содержащих три значащих цифры: 23,5; 0,0314; 40,0.
8. Помните, что точность результата вычислений не может быть выше, чем точность исходных данных. Это означает, что в полученном результате следует оставить столько значащих цифр, сколько их содержится в наименее точном числе исходных данных задачи.
Рекомендации по выполнению расчетов при решении задач
1. Полученную расчетную формулу проверьте на совпадение единиц измерения искомой величины (в левой и правой части формулы). Это можно сделать как перед вычислениями (в случае получения расчетной формулы долгим путем, в котором велика вероятность появления ошибки), так и непосредственно при подстановке величин в расчетную формулу.
2. Выполняя вычисления, в расчетную формулу подставляйте значения величин с указанием их единиц (независимо от того, была ли сделана предварительная проверка формулы по единицам величин, или нет). Это необходимо делать для того, чтобы убедиться, что все исходные данные взяты в единицах одной системы – системы СИ. При подстановке величин кратные и дольные приставки к единицам (кило-, милли-, нано- и др.) заменяйте соответствующими сомножителями .
3. Отдельно вычислите произведение чисел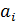 
, стоящих перед сомножителями , и полученный результат (величину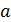 
) сразу (при записи с экрана микрокалькулятора) округлите до 3-х значащих цифр. Затем отдельно вычислите произведение сомножителей . Напомним правила работы с показателями степеней.
При перемножении чисел показатели степеней складываются (так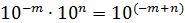 
).
При делении чисел показатели вычитаются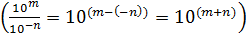 
.
При возведении числа в степень показатели степени перемножаются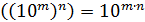 
, например, 
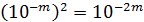, или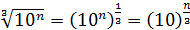 
.
Замечание: при возведении в дробную степень (например, при извлечении корня), чтобы получить целочисленный показатель степени, следует предварительно сделать показатель степени подкоренного выражения кратным 2 (для квадратного корня) или 3 (в случае кубического корня). Например,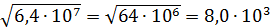 
; или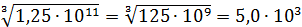 
.
4. Число, полученное при вычислениях в виде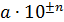 
, приведите а) к общепринятому виду, в котором сомножитель 
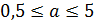, либо б) к виду, удобному для введения приставки к единице измерения искомой величины. Так 
; 
.
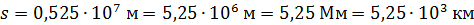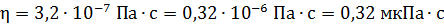Приведем примеры.
1. В решении задачи получена расчетная формула для определения момента инерции маховика динамическим методом:
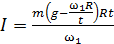, или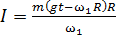 
.
Проверим формулу по единицам измерения величин:
.
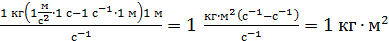Получили единицу измерения момента инерции I, следовательно, расчетная формула верна. Вычисляем по ней момент инерции маховика
.
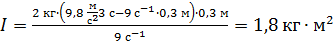2. При решении одной из задач получена следующая расчетная формула для высоты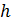 
, на которую поднимется поршень в изобарическом процессе расширения газа
.
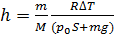Вычислим перемещение поршня при нагреве газа по формуле (6):
.
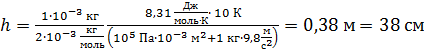Примечание:
Результат вычисления записывайте с точностью до двух или трех (не более) значащих цифр. Значащими являются все верные цифры числа, кроме нулей, стоящих перед первой ненулевой цифрой (заметим, что значащие цифры могут быть записаны как до запятой, отделяющей целую часть от дробной, так и после нее). Приведем примеры чисел, содержащих три значащих цифры: 123; 3,45; 0,0216; 20,0 и т. п.
Незначащие нули записывайте в виде сомножителя . При этом, если показатель степени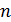 
соответствует приставке, то используйте её: например, 
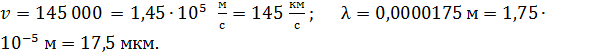Помните, что точность результата вычислений не может быть выше, чем точность исходных данных: если величины в условии задачи содержат 2 значащие цифры, то в результате вычислений верными будут только 2 значащие цифры (остальные будут ложными и поэтому их не указывают).
В случае затруднений при использовании приставок (они указаны в табл. 1 приложения) или при работе с множителями , постарайтесь усвоить следующие простые правила.
Разбивая число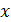 
на два сомножителя: 
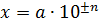, – величину 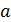выбирают в интервале (0,5…5,0), при этом показатель степени 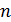показывает порядок величины числа 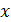. Если же для искомой физической величины традиционно используют приставки (например, длину волны света 
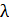принято выражать в микрометрах (мкм)), то выбирайте значение 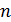соответствующим ближайшей приставке, которая обычно кратна трем, –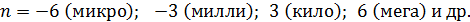 
Если при таком пересчете множитель пришлось уменьшить в 10 раз, то необходимо увеличить в 10 раз второй сомножитель – 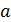, чтобы число 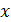не изменилось; и наоборот: увеличивая множитель , например, в 100 раз, уменьшайте в 100 раз сомножитель .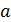
Приведем примеры: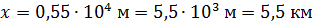 
; 
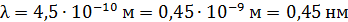. Запись величины 
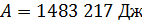является неграмотной, так как показывает, что величина работы 
определена с точностью до 7 значащих цифр; не менее ошибочна и запись этой величины в виде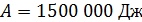 
, так как округление величины не уменьшило число значащих цифр (5 нулей являются значащими). Правильной является запись 
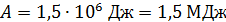(если в исходных данных две значащих цифры), либо 
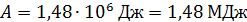, если при вычислении величины использовали данные с тремя значащими цифрами.
Приведем пример решения и оформления задачи при выполнении контрольной работы.
1.8. Пример решения и оформления задачи контрольной работы
Задача 102. Материальная точка вращается вокруг неподвижной оси по закону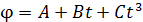 
, где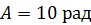 
, 
, 
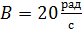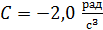. Определите полное ускорение точки, находящейся на расстоянии 
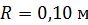от оси вращения, для момента времени 
.
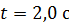Дано
;
;
;
;
;
.
| ||
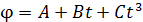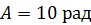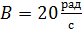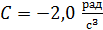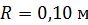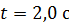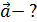
Решение
Вращающаяся точка движется по окружности; при этом ее полное ускорение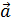 
равно сумме векторов ускорений – тангенциального 
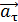, направленного по касательной к траектории, и нормального ускорения 
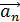, направленного к центру кривизны траектории:
.
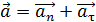Так как векторы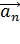 
и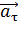 
взаимно перпендикулярны, то модуль ускорения
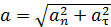. (1)
Линейные ускорения материальной точки: нормальное и тангенциальное, – связаны с угловыми величинами следующими формулами:
; 
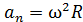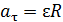, (2)
где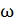 
– угловая скорость точки; 
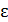– ее угловое ускорение.
Подставляя выражения (2) в формулу (1), получаем расчетную формулу в виде:
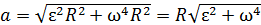. (3)
|
|
|
|
|
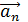
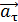
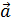
Угловую скорость 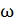находим, как первую производную от угла поворота по времени:
.
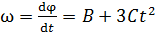В момент времени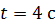 
модуль угловой скорости
.
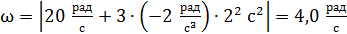Угловое ускорение равно первой производной от угловой скорости по времени:
.
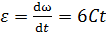Его модуль в момент времени :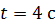
.
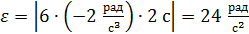Подставляя значения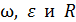 
в формулу (3) вычисляем линейное ускорение материальной точки:
.
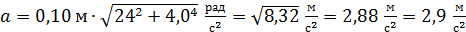Библиографический список
1. Трофимова, Т.И. Курс физики: учебное пособие для инженерно-технических специальностей вузов / Т.И. Трофимова. – М.: Академия, 2010. – 557 с.
2. Писарев, Н.М. Физика: Курс лекций для студентов инженерных специальностей вузов / Н.М. Писарев; под ред. Г.П. Вяткина. – Челябинск: Изд-во ЧГТУ, 1997. – Ч.1. – 171 с. Ч.2. – 299 с.
3. Детлаф, А.А. Курс физики: учебное пособие для втузов / А.А. Детлаф, Б.М. Яворский. – М.: Академия, 2008. – 719 с.
4. Савельев, И.В. Курс физики Т.1: Механика. Т.2: Электричество и магнетизм. Т.3: Молекулярная физика: учебное пособие для втузов: в 5 т. / И.В. Савельев. – СПб. и др.: Лань, 2011. – 342 с.
5. Савельев, И.В. Курс физики Т.3: Молекулярная физика: учебное пособие для втузов: в 5 т. / И.В. Савельев. – СПб. и др.: Лань, 2008. – 208 с.
6. Механика и молекулярная физика. Руководство к решению задач: учебное пособие для студентов вузов / В.К. Герасимов, Т.О. Миронова, Ю.Б. Пейсахов, Т.П. Привалова. – Челябинск: Издательский центр ЮУрГУ, 2014. – 83 с. http://physics.susu.ac.ru/data/ mechanics.pdf.
7. Чертов, А.Г. Задачник по физике: учебное пособие для втузов / А.Г. Чертов, А.А. Воробьев. – М.: Издательство Физматлит, 2008. – 640 с.
8. Иродов, И.Е. Задачи по общей физике: учебное пособие для втузов / И.Е. Иродов. – СПб. и др.: Лань, 2009. – 431 с.
9. Фирганг, Е.В. Руководство к решению задач по курсу общей физики: учебное пособие для втузов по техническим и технологическим направлениям / Е.В. Фирганг. – СПб. и др.: Лань, 2009. – 347 с.
10. Механика и молекулярная физика: учебное пособие к выполнению лабораторных работ / В.К. Герасимов, А.Е. Гришкевич, С.И. Морозов и др.; под ред. В.П. Бескачко. – Челябинск: Изд-во ЮУрГУ, 2008. – 95 с.
11. Механика и молекулярная физика: учебное пособие к выполнению лабораторных работ / В.К. Герасимов, А.Е. Гришкевич, С.И. Морозов и др.; под ред. В.П. Бескачко. – Челябинск: Изд-во ЮУрГУ, 2008. – 95 с. http://physics.susu.ac.ru/data/mechanics.pdf.
12. Герасимов, В.К. Физика. Т.1: Механика и молекулярная физика. Учебное пособие по физике: выполнение контрольных и лабораторных работ; в 3 т. / В.К. Герасимов, Т.О. Миронова, Ю.Б. Пейсахов, Т.П. Привалова. – 125 с. Сайт ЗИЭФ ЮУрГУ – http://zief.susu.ac.ru.
13. Герасимов, В.К. Физика. Т.2: Электромагнетизм. Учебное пособие по физике: выполнение контрольных и лабораторных работ; в 3 т. / В.К. Герасимов, Т.О. Миронова, Ю.Б. Пейсахов, Т.П. Привалова. – 140 с. Сайт ЗИЭФ ЮУрГУ – http://zief.susu.ac.ru.
КОНТРОЛЬНАЯ РАБОТА № 1
Студент ЗИЭФ решает 6 задач своего варианта, номер которого совпадает с последней цифрой его шифра. Номера задач каждого варианта представлены в табл. 4.
2.1. Таблица вариантов контрольной работы № 1
Таблица 4
| Вариант | Номера задач | |||||
| 0 | 110 | 120 | 130 | 140 | 150 | 160 |
| 1 | 101 | 111 | 121 | 131 | 141 | 151 |
| 2 | 102 | 112 | 122 | 132 | 142 | 152 |
| 3 | 103 | 113 | 123 | 133 | 143 | 153 |
| 4 | 104 | 114 | 124 | 134 | 144 | 154 |
| 5 | 105 | 115 | 125 | 135 | 145 | 155 |
| 6 | 106 | 116 | 126 | 136 | 146 | 156 |
| 7 | 107 | 117 | 127 | 137 | 147 | 157 |
| 8 | 108 | 118 | 128 | 138 | 148 | 158 |
| 9 | 109 | 119 | 129 | 139 | 149 | 159 |
Дата: 2019-11-01, просмотров: 214.
