| А |
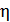 неупругого удара бойка массой
неупругого удара бойка массой 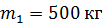 , падающего на сваю массой
, падающего на сваю массой 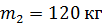 . Полезной считайте энергию, пошедшую на вбивание сваи.
. Полезной считайте энергию, пошедшую на вбивание сваи.
11. Шар массой 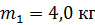 движется со скоростью
движется со скоростью 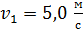 и сталкивается с шаром массой
и сталкивается с шаром массой 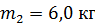 , который движется ему навстречу со скоростью
, который движется ему навстречу со скоростью 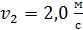 . Считая удар прямым и центральным, а шары абсолютно упругими, найдите их скорости
. Считая удар прямым и центральным, а шары абсолютно упругими, найдите их скорости 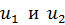 после удара.
после удара.
12. Орудие, закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом 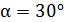 к линии горизонта. Определите скорость
к линии горизонта. Определите скорость 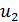 отката платформы, если снаряд вылетает со скоростью
отката платформы, если снаряд вылетает со скоростью 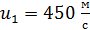 . Масса платформы с орудием и снарядами
. Масса платформы с орудием и снарядами 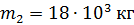 , масса снаряда
, масса снаряда 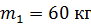 .
.
13. Шарик массой 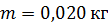 , движущийся со скоростью
, движущийся со скоростью 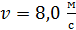 под углом
под углом 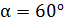 к плоскости стенки, упруго ударяется о стенку. Определите импульс
к плоскости стенки, упруго ударяется о стенку. Определите импульс 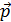 , полученный стенкой при ударе шарика.
, полученный стенкой при ударе шарика.
14. Снаряд массой 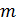 , летевший со скоростью
, летевший со скоростью 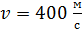 , разорвался на два осколка. Меньший осколок, масса которого
, разорвался на два осколка. Меньший осколок, масса которого 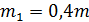 , полетел в противоположном направлении со скоростью
, полетел в противоположном направлении со скоростью 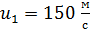 . Определите скорость
. Определите скорость 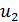 большего осколка.
большего осколка.
15. В деревянный шар массой 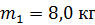 , подвешенный на нити длиной
, подвешенный на нити длиной 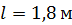 , попадает горизонтально летящая пуля массой
, попадает горизонтально летящая пуля массой 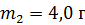 . С какой скоростью
. С какой скоростью 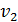 летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол
летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол 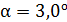 ? Размером шара можно пренебречь. Удар пули считайте прямым и центральным.
? Размером шара можно пренебречь. Удар пули считайте прямым и центральным.
16. По небольшому куску мягкого железа, лежащему на наковальне массой 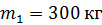 , ударяет молот массой
, ударяет молот массой 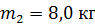 . Определите КПД удара
. Определите КПД удара 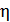 , если удар неупругий. Полезной считайте энергию, пошедшую на деформацию куска железа.
, если удар неупругий. Полезной считайте энергию, пошедшую на деформацию куска железа.
17. Шар массой 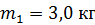 движется со скоростью
движется со скоростью 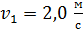 и соударяется с покоящимся шаром массой
и соударяется с покоящимся шаром массой 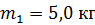 . Какая работа совершается при деформации шаров? Удар считайте абсолютно неупругим, прямым и центральным.
. Какая работа совершается при деформации шаров? Удар считайте абсолютно неупругим, прямым и центральным.
18. Конькобежец массой 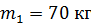 , стоя на коньках на льду, бросает в горизонтальном направлении камень массой
, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 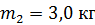 со скоростью
со скоростью 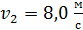 . Определите скорость
. Определите скорость 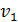 конькобежца после броска, работу
конькобежца после броска, работу  , совершенную им при броске, и расстояние
, совершенную им при броске, и расстояние 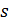 , на которое он откатился, если коэффициент трения коньков о лед
, на которое он откатился, если коэффициент трения коньков о лед 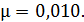
19. Вентилятор вращается с частотой 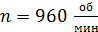 . После выключения мотора вентилятор, вращаясь равнозамедленно, сделал до остановки
. После выключения мотора вентилятор, вращаясь равнозамедленно, сделал до остановки 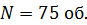 Работа сил торможения
Работа сил торможения 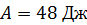 . Определите: 1) угловое ускорение вентилятора
. Определите: 1) угловое ускорение вентилятора 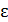 ; 2) момент силы торможения
; 2) момент силы торможения 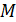 и 3) момент инерции вентилятора
и 3) момент инерции вентилятора 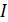 .
.
20. С какой наименьшей высоты 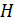 должен съехать велосипедист, чтобы по инерции (без трения) проехать дорожку, имеющую форму «мертвой петли» радиусом
должен съехать велосипедист, чтобы по инерции (без трения) проехать дорожку, имеющую форму «мертвой петли» радиусом 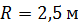 , и не оторваться от дорожки в верхней точке петли? Масса велосипедиста вместе с велосипедом
, и не оторваться от дорожки в верхней точке петли? Масса велосипедиста вместе с велосипедом 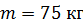 , включая массу колес
, включая массу колес 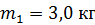 . Колеса велосипеда считайте обручами.
. Колеса велосипеда считайте обручами.
21. Определите линейное ускорение 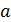 движения центра тяжести шара, скатывающегося с наклонной плоскости. Угол наклона плоскости
движения центра тяжести шара, скатывающегося с наклонной плоскости. Угол наклона плоскости 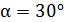 , начальная скорость шара равна нулю.
, начальная скорость шара равна нулю.
22. Два шара, подвешенные на параллельных нитях одинаковой длины, соприкасаются. Масса первого шара 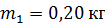 , масса второго
, масса второго 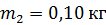 . Первый шар отклонили так, что его центр тяжести оказался на высоте
. Первый шар отклонили так, что его центр тяжести оказался на высоте 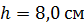 , и отпустили. На какую высоту
, и отпустили. На какую высоту 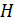 поднимутся шары после их неупругого соударения? Определите изменение энергии
поднимутся шары после их неупругого соударения? Определите изменение энергии 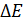 шаров при ударе.
шаров при ударе.
23. Стержень длиной 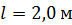 , подвешенный на горизонтальной оси, проходящей через верхний конец стержня, отклонили от вертикали на угол
, подвешенный на горизонтальной оси, проходящей через верхний конец стержня, отклонили от вертикали на угол 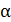 и отпустили. Определите угол
и отпустили. Определите угол 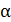 , при котором скорость конца стержня при прохождении им положения равновесия
, при котором скорость конца стержня при прохождении им положения равновесия 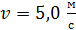 .
.
24. Тело скользит по наклонной плоскости, составляющей с горизонтом угол 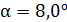 , а затем по горизонтальной поверхности. Найдите коэффициент трения
, а затем по горизонтальной поверхности. Найдите коэффициент трения 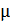 (он одинаков на обоих участках пути), если известно, что тело проходит по горизонтали такое же расстояние
(он одинаков на обоих участках пути), если известно, что тело проходит по горизонтали такое же расстояние 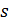 , как и по наклонной плоскости.
, как и по наклонной плоскости.
25. Мальчик катит обруч по горизонтальной поверхности со скоростью 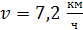 . На какое расстояние
. На какое расстояние 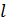 может вкатиться обруч на горку за счет своей кинетической энергии, если уклон горки составляет
может вкатиться обруч на горку за счет своей кинетической энергии, если уклон горки составляет 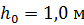 на пути
на пути 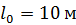 .
.
Закон сохранения момента импульса (ЗСМИ)
26. Горизонтальная платформа массой 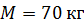 и радиусом
и радиусом 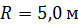 вращается свободно относительно вертикальной оси с частотой
вращается свободно относительно вертикальной оси с частотой 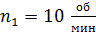 . Человек массой
. Человек массой 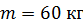 стоит на краю платформы. С какой частотой
стоит на краю платформы. С какой частотой 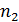 будет вращаться платформа, если человек перейдет от края платформы к ее центру? Какую работу
будет вращаться платформа, если человек перейдет от края платформы к ее центру? Какую работу  совершит человек при переходе? Момент инерции платформы рассчитайте, как диска, а человека – как материальной точки.
совершит человек при переходе? Момент инерции платформы рассчитайте, как диска, а человека – как материальной точки.
27. Диск радиусом 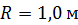 и массой
и массой 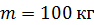 вращается с частотой
вращается с частотой 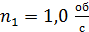 . В центре диска стоит человек и держит гири в вытянутых в стороны руках. Определите угловую скорость
. В центре диска стоит человек и держит гири в вытянутых в стороны руках. Определите угловую скорость 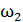 вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от величины
вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от величины 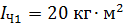 до
до 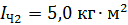 . Какую работу
. Какую работу  совершит человек?
совершит человек?
28. Платформа (диск) радиусом 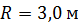 и массой
и массой 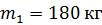 может вращаться без трения вокруг вертикальной оси. С какой угловой скоростью
может вращаться без трения вокруг вертикальной оси. С какой угловой скоростью 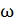 будет вращаться платформа, если по ее краю пойдет человек массой
будет вращаться платформа, если по ее краю пойдет человек массой 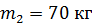 со скоростью
со скоростью 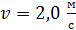 относительно платформы?
относительно платформы?
29. На неподвижной скамье Жуковского стоит человек и ловит рукой мяч массой 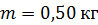 , который летит горизонтально со скоростью
, который летит горизонтально со скоростью 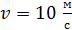 . С какой угловой скоростью
. С какой угловой скоростью 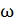 будет вращаться скамья с человеком, поймавшим мяч? Расстояние мяча от оси вращения скамьи
будет вращаться скамья с человеком, поймавшим мяч? Расстояние мяча от оси вращения скамьи 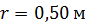 . Момент инерции скамьи с человеком
. Момент инерции скамьи с человеком 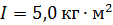 .
.
30. Человек стоит в центре скамьи Жуковского и держит в руках стержень, расположенный вертикально вдоль оси вращения скамьи. Скамья с человеком вращается с угловой скоростью 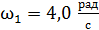 . С какой угловой скоростью
. С какой угловой скоростью 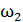 будет вращаться скамья с человеком, если он расположит стержень горизонтально так, что его центр масс будет на оси скамьи. Момент инерции скамьи с человеком
будет вращаться скамья с человеком, если он расположит стержень горизонтально так, что его центр масс будет на оси скамьи. Момент инерции скамьи с человеком 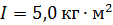 . Длина стержня
. Длина стержня 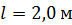 , его масса
, его масса 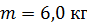 .
.
31. Диск радиусом 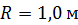 и массой
и массой 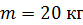 вращается с угловой скоростью
вращается с угловой скоростью 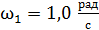 . В центре диска стоит человек и держит в вытянутых в стороны руках гири массой
. В центре диска стоит человек и держит в вытянутых в стороны руках гири массой 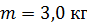 каждая; расстояние гирь от оси вращения
каждая; расстояние гирь от оси вращения 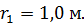 Определите угловую скорость
Определите угловую скорость 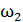 вращения платформы, если человек, опустив руки, уменьшит расстояние гирь от оси до
вращения платформы, если человек, опустив руки, уменьшит расстояние гирь от оси до 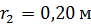 . Момент инерции человека относительно оси вращения
. Момент инерции человека относительно оси вращения 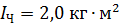 . Какую работу
. Какую работу  совершит человек?
совершит человек?
32. Человек стоит на неподвижной скамье Жуковского и держит стержень, расположенный вертикально вдоль оси вращения скамьи. На конце стержня вращается колесо с частотой 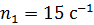 . Определите угловую скорость вращения скамьи
. Определите угловую скорость вращения скамьи 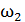 , когда человек повернет стержень с колесом на угол
, когда человек повернет стержень с колесом на угол 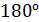 . Суммарный момент инерции скамьи с человеком
. Суммарный момент инерции скамьи с человеком 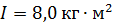 . Радиус колеса
. Радиус колеса 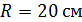 , а его масса
, а его масса 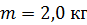 равномерно распределена по ободу.
равномерно распределена по ободу.
Механические колебания
33. Пружинный маятник жесткостью 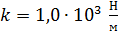 совершает гармонические колебания. Масса груза
совершает гармонические колебания. Масса груза 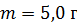 , его максимальная скорость
, его максимальная скорость 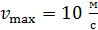 . Определите циклическую частоту
. Определите циклическую частоту 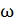 и период колебаний груза
и период колебаний груза 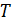 , а также амплитуду колебаний
, а также амплитуду колебаний  .
.
34. Частица массой 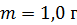 совершает гармонические колебания по закону
совершает гармонические колебания по закону 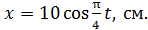 Определите циклическую частоту
Определите циклическую частоту 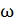 , период колебаний
, период колебаний 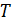 , максимальную скорость частицы
, максимальную скорость частицы 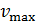 и ее полную механическую энергию
и ее полную механическую энергию 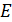 .
.
35. Материальная точка (МТ) массой 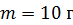 совершает колебания по гармоническому закону
совершает колебания по гармоническому закону 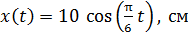 . Определите амплитуду
. Определите амплитуду  и период
и период 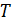 колебаний МТ, а также модуль ее скорости
колебаний МТ, а также модуль ее скорости 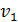 в момент времени
в момент времени 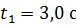 .
.
Дата: 2019-11-01, просмотров: 347.