Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Сравнение с теорией. Функциональные шкалы

Для проверки теоретической зависимости на график наносят опытные точки (нередко с указанием их погрешности в виде –D_Y), а теоретическую кривую проводят через точки, рассчитанные по уравнению. Если теория дает лишь вид зависимости, а параметры ее неизвестны и их надлежит определить из опыта, то экспериментальную зависимость стараются привести к линейному виду (так как параметры прямой найти проще). С этой целью при построении графика по осям откладывают не сами измеренные величины, а такие функции этих величин, которые позволяют линеаризовать зависимость. Рассмотрим пример.

Опыт показывает, что электрическое сопротивление полупроводника снижается с ростом температуры нелинейно. Чтобы выбрать координаты, в которых зависимость линеаризуется, обратимся к теории. Согласно квантовой теории твердого тела сопротивление истинного полупроводника меняется с температурой по закону 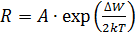. Логарифмируя это уравнение, получаем зависимость 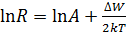, которая представится на графике в виде прямой 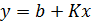, если обозначить 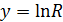, 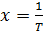. Определяя параметры этой прямо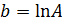й  и 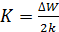, можно найти характеристики полупроводника .

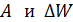Определение параметров линейной зависимости

  Известны два наиболее распространенных метода:

– приближенный метод определения параметров прямой, использующий отрезки, отсчитанные по шкале на осях графика;

– метод наименьших квадратов (МНК).

Приближенный метод

  Пусть измеренные величины 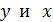 связаны линейной зависимостью вида  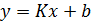  и   требуется определить ее параметры .

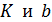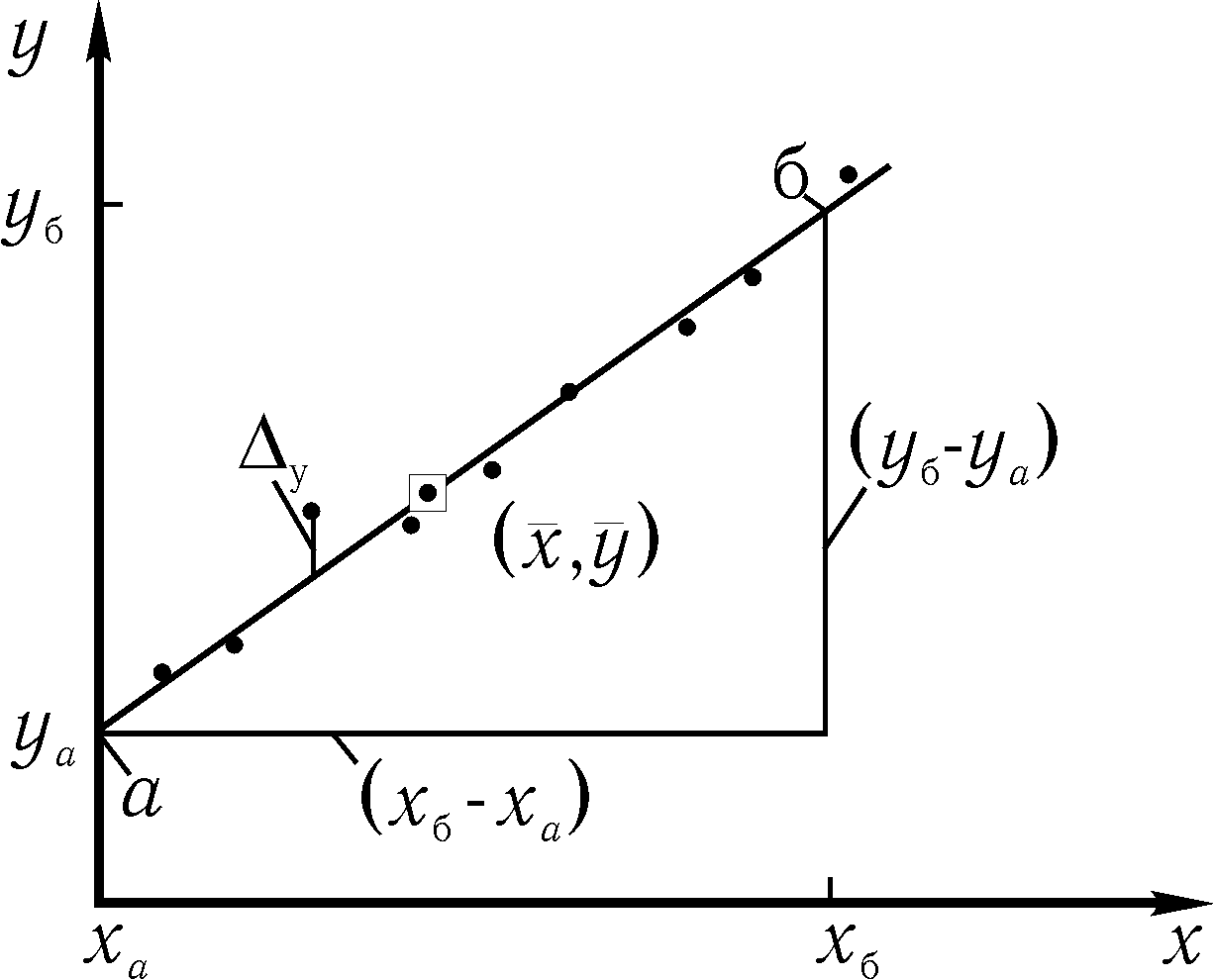Рис. 4. Определение параметров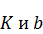

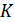  Для этого опытные точки наносят на график и проводят прямую линию, руководствуясь правилами построения графика. На концах линии выбирают две произвольные точки a и б,удобные для расчета. Чтобы снизить погрешность отсчета по графику и упростить расчет углового коэффициента , удобно точку а взять на одной из осей, а точку б – так, чтобы отрезок  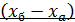выражался целым числом.

  Среднее значение углового коэффициента 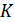 вычисляют как отношение, определяющее наклон прямой:

.

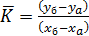  Параметр b линейной зависимости находят по графику как ординату точки пересечения прямой с осью 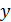. Величину  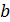можно найти и по уравнению прямой, подставляя координаты средней точки графика:

.

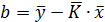  Случайные погрешности параметров определяются разбросом опытных точек по отношению к проведенной прямой. Для простейшей оценки этих погрешностей достаточно найти на графике величину 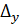 – отклонение наиболее удаленной точки от прямой линии, и  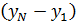– интервал, в котором сделаны измерения (длина оси ).

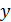  Абсолютная случайная погрешность параметра b: .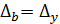

  Для углового коэффициента прямой линии 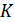 сначала вычисляют относительную погрешность:

.

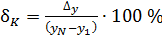Эта формула привлекает тем, что при расчете отношения величин одного рода можно взять их в любых единицах (всего удобнее – в малых делениях шкалы оси 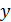). Напомним, что в величине погрешности имеет значение, как правило, одна цифра, а потому достаточная точность отсчета отрезка  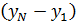– "круглое число", например, 90, 100 или 120 мм (или 10 – 15 клеток масштабной бумаги).

  Затем находят абсолютную погрешность средней величины :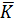

,

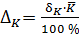чтобы записать доверительный интервал для искомого параметра :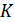

.

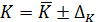  Доверительная вероятность 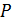 в описанном методе оценки погрешностей (по максимальному отклонению 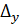) зависит от числа опытных точек  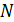– чем больше число 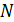, тем выше надежность результата:

.

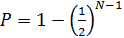Темы лабораторных работ

Таблица 5

Название работы	Номер работы в  учебном пособии
1. Изучение динамики вращательного движения	3
2. Определение ускорения свободного падения с помощью оборотного и математического маятников	7
3. Определение отношения теплоемкостей воздуха	12

Подготовка к выполнению лабораторных работ

  Методические указания к выполнению лабораторных работ: описание метода измерений, лабораторного стенда, порядок выполнения ЛР и обработки результатов измерений, – содержатся в следующем учебном пособии:

Механика и молекулярная физика: учебное пособие к выполнению лабораторных работ / В.К. Герасимов, А.Е. Гришкевич, С.И. Морозов и др.; под ред. В.П. Бескачко. – Челябинск: Изд-во ЮУрГУ, 2008. – 95 с.  

  Данное учебное пособие можно найти по следующему электронному адресу: http :// physics . susu . ac . ru / data / mechanics . pdf .

  При подготовке к занятию в лаборатории настоятельно рекомендуем по каждой выполняемой ЛР заполнить некоторые разделы бланка отчета  (до таблиц опытных данных): цель работы, описание установки и метода измерений (включая название величин, входящих в расчетные формулы). Это позволит Вам получить представление о лабораторной работе и, благодаря этому, избежать ненужных ошибок при проведении эксперимента в физической лаборатории.

  Перед выполнением лабораторных работ необходимо изучить раздел 3.1 «Введение в лабораторный практикум по физике» (с. 40-47) – п. п. 3.1.1. Проведение лабораторного эксперимента и 3.1.2. Графическое представление и обработка результатов измерений.

3.3.1. Рекомендации к выполнению лабораторных работ