Результаты измерений представляют в виде таблиц, графиков и уравнений. В каждом эксперименте необходимо сразу же записывать результаты измерений аккуратно в заранее заготовленные таблицы. Записи в таблице должны быть удобны для чтения и обработки, что достигается выполнением ряда правил.
1. Значения каждой величины записывайте в соответствующий столбец одно под другим так, чтобы одинаковые разряды чисел и запятые располагались на одной вертикали: так легче сопоставить числа. Избегайте исправления цифр: это затрудняет чтение. Лучше зачеркнуть неверные цифры, а правильные написать рядом.
2. В заголовке таблицы для каждого столбца указывают обозначение величины и через запятую её единицу. Не нужно писать единицы величин в каждой строке таблицы: это потеря времени и загромождение записи. Данные прямых измерений и приборные погрешности записывают в единицах шкалы приборов, а результаты расчёта приводят обычно в единицах СИ.
3. Для сокращения записи чисел используют десятичный множитель  . Его величину часто берут соответствующей краткой приставке (микро-, мили-, кило- и т. п.). Этот множитель, общий для всех значений в столбце, указывают вместе с единицей величины в заголовке таблицы. При этом используют два разных варианта записи множителя. Примеры приведены в таблице, где записана вязкость газов двумя способами.
. Его величину часто берут соответствующей краткой приставке (микро-, мили-, кило- и т. п.). Этот множитель, общий для всех значений в столбце, указывают вместе с единицей величины в заголовке таблицы. При этом используют два разных варианта записи множителя. Примеры приведены в таблице, где записана вязкость газов двумя способами.
Первый способ, при котором после символа величины ставят запятую, а множитель относят к единице величины ( 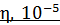 Па × с), воспринимается естественно и является предпочтительным.
Па × с), воспринимается естественно и является предпочтительным.
Второй способ нередко встречается в справочных таблицах, и при их чтении нужно обращать внимание, нет ли знака умножения. Так, запись 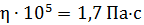 означает, что
означает, что 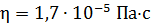 .
.
| Газ | Вязкость
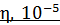 Па × с Па × с
| Вязкость
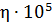 , Па×с , Па×с
| |
|
Воздух Водород | 1,72 0,84 | 1,72 0,84 |
Графическое представление и обработка результатов измерений
Построение графиков
Назначение графика – наглядно представить результаты опыта при изучении зависимости одной величины от другой. График позволяет увидеть особенности исследуемой зависимости, выявить ее характер (линейная, квадратичная или экспоненциальная) и определить параметры. Все это становится доступным при грамотном применении графического метода, а для этого необходимо следовать определенным правилам построения графиков и использовать методы их обработки.
1. Выбор координатных осей. График выполняют на листе миллиметровой бумаги размером 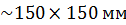 ; координатные оси берут примерно равной длины. Горизонтальная ось отводится аргументу, т. е. величине, значение которой задает сам экспериментатор, а вертикальная ось – функции. В конце каждой оси указывают символ величины, десятичный множитель и единицу величины. При этом десятичный множитель
; координатные оси берут примерно равной длины. Горизонтальная ось отводится аргументу, т. е. величине, значение которой задает сам экспериментатор, а вертикальная ось – функции. В конце каждой оси указывают символ величины, десятичный множитель и единицу величины. При этом десятичный множитель 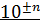 позволяет опустить нули при нанесении шкалы, например, писать 1; 2; 3 ... вместо 0,001; 0,002 и т.д.
позволяет опустить нули при нанесении шкалы, например, писать 1; 2; 3 ... вместо 0,001; 0,002 и т.д.
2. Выбор интервалов. Интервалы чисел на каждой оси выбирают независимо друг от друга, причем такие, чтобы кривая заняла все поле чертежа. Для этого границы интервалов берут близкими к наименьшему и наибольшему среди измеренных значений. Подчеркнем, что начало отсчета часто начинают не с нуля. Нулевую точку помещают на график лишь в том случае, если она близка к экспериментально исследованной области или необходима экстраполяция на нулевое значение.
3. Выбор масштабов и шкалы. Масштаб должен быть простым и удобным для нанесения точек на график. За единицу масштаба принимают отрезок оси, кратный 5, 10, 50 или 100 мм, что позволяет легко отсчитывать доли отрезка. Такому отрезку соотносят "круглое" число (1, 2, 5) единиц измеряемой величины. Деления шкалы на каждой оси подбирают независимо, в соответствии с масштабом, причем надписи делений наносят вдоль всей оси. Чтобы шкала легко читалась, достаточно указать на оси 3–5 чисел.
4. Нанесение точек. Опытные данные наносят на поле графика в виде четких значков, не подписывая их численные значения – они приводятся только в таблице. Разные значки (светлые и темные кружки, треугольники и др.) используют для обозначения данных, относящихся к различным условиям.
5. Проведение экспериментальной кривой. Кривую проводят плавной, непрерывной линией (таковы обычно физические зависимости) так, чтобы точки находились равномерно по обе стороны кривой как можно ближе к ней. Если вид зависимости известен заранее, то проводят эту теоретическую кривую.
Для линейной зависимости: прямую проводят через среднюю точку, координаты которой определяют по следующим формулам:
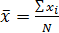 ;
; 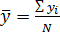 .
.
Здесь записаны суммы 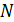 слагаемых измеренных величин;
слагаемых измеренных величин; 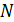 – общее число точек на графике.
– общее число точек на графике.
6. Заголовок графика. График сопровождают названием зависимости, в котором называют символы величин, указанные в конце осей. Кроме того, в подписи к графику разъясняют обозначения опытных точек и кривых, если их несколько. Заголовок принято располагать выше графика, либо под графиком.
Дата: 2019-11-01, просмотров: 361.