ФИЗИКА
Практическое руководство для самостоятельной работы
студентов заочной формы обучения ПИ ЮУрГУ
Челябинск
Издательский центр ЮУрГУ
2018
УДК 530.1(075.8)
М641
Одобрено
учебно-методической комиссией Института
естественных и точных наук
Рецензенты:
Л.А. Песин, В.К. Усачев
Миронова Т.О.
М.641 Физика: практическое руководство для самостоятельной работы студентов заочной формы обучения ПИ ЮУрГУ / Т.О. Миронова, Ю.Б. Пейсахов, Т.П. Привалова. – Челябинск: Издательский центр ЮУрГУ, 2018. – 124 с.
Основное назначение учебного пособия – оказать помощь по изучению курса общей физики студентам заочной формы обучения. Учебное пособие является руководством в организации работы студентов в течение двух семестров. В пособии даны программные вопросы по курсу физики, варианты и задачи контрольных работ, изложены требования к выполнению контрольных работ и к оформлению решений задач, а также содержатся методические материалы для выполнения лабораторных работ и рекомендации по оформлению отчетов.
Учебное издание предназначено для студентов, обучающихся по укрупненным группам специальностей и направлений подготовки в области образования «инженерное дело, технологии и технические науки».
УДК 530.1(075.8)
© Издательский центр ЮУрГУ, 2018
ОГЛАВЛЕНИЕ
Введение ….…………………………………………………………… . . . . 5
Часть I
МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА.
ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
(3-й семестр обучения)
1.1. Программные (экзаменационные) вопросы . …………………………7
1.2. Типовые задачи (экзаменационные) ..………………………………..11
1.3. Установочные лекции ..……………………………….. ..…………….24
1.4. Самостоятельная работа студентов . . . . . . …………………………...24
1.5. Требования к оформлению решения задач контрольной работы ......25
1.6. Рекомендации к решению физических задач ...……………………26
1.7. Рекомендации по выполнению расчетов при решении задач ………27
1.8. Пример решения и оформления задачи контрольной работы ..……29
Библиографический список …..……………………….…………………..31
2. КОНТРОЛЬНАЯ РАБОТА № 1 ….……………………………………32
2.1. Таблица вариантов контрольной работы № 1 ……………………….32
2.2. Задачи контрольной работы № 1 ....………………………………..…32
3. ЛАБОРАТОРНЫЕ РАБОТЫ ПО МЕХАНИКЕ, МФ И ТД
3.1. Введение в лабораторный практикум по физике
3.1.1. Проведение лабораторного эксперимента
Результат измерения и погрешности …………………………………40
Систематические и случайные погрешности ………………………..40
Приборная погрешность ………………………………………………41
Вычисления и запись результата ……………………………………..42
Представление результатов измерений в виде таблиц ………………43
Графическое представление и обработка результатов измерений
Построение графиков …………………………………………………44
Графический анализ опытных данных. Сравнение с теорией.
Функциональные шкалы . . . . ………...………………………………45
Определение параметров линейной зависимости …………………..45
3.2. Темы лабораторных работ …………………………………………….47 3.3. Подготовка к выполнению лабораторных работ ……………………..47
3.3.1. Рекомендации к выполнению лабораторных работ ……………….48
3.3.2. Рекомендации к оформлению отчета по лабораторной работе …..48
3.3.3. Бланки отчетов по лабораторным работам ………………………..49
Часть II
ЭЛЕКТРОМАГНЕТИЗМ. ОПТИКА. ФИЗИКА АТОМА И ЯДЕРНАЯ ФИЗИКА
(4-й семестр обучения)
4.1. программные (экзаменационные) вопросы ..…………………………62
4.2. Типовые задачи (экзаменационные) ..………………………………..66
4.3. Установочные лекции ……………………………………………….80
4.4. Самостоятельная работа студентов ………………………………….81
Библиографический список ………….……………….….……………….81
5. КОНТРОЛЬНАЯ РАБОТА № 2 ………………………………………..82
5.1. Таблица вариантов контрольной работы № 2 .…………………….82
5.2. Рекомендации к решению задач по разделу «Электромагнетизм» …83
5.3. Задачи контрольной работы № 2 ...………………………………….83
6. КОНТРОЛЬНАЯ РАБОТА № 3 ………………………………………91
6.1. Таблица вариантов контрольной работы № 3 ………………………91
6.2. Рекомендации к решению задач по разделу «Оптика» ...……………91
6.3. Рекомендации к решению задач по разделу «Атомная и ядерная
физика» ....………………………………………………………………92
6.4. Задачи контрольной работы № 3 ………………………………….... 93
7. ЛАБОРАТОРНЫЕ РАБОТЫ ПО ЭЛЕКТРОМАГНЕТИЗМУ
7.1. Темы лабораторных работ ....………………………………………….99
7.2. Подготовка к выполнению лабораторных работ ...…………………..99
7.3. Бланки отчетов по лабораторным работам ..………………………100
ПРИЛОЖЕНИЯ
Приложение 1. Справочные данные по математике и физике
О приближенных вычислениях ….....……………………………………111
Некоторые формулы алгебры и тригонометрии …....…………………111
Основные формулы дифференцирования и интегрирования …......…..111
Формулы приближенных вычислений .………………………………...112
Единицы физических величин в СИ ..…………………………………...113
Множители и приставки для образования кратных и дольных единиц ...116
Приложение 2. Таблицы физических величин (справочные) ………....117
ВВЕДЕНИЕ
Методические указания адресованы студентам заочного факультета (ЗИЭФ) политехнического института ЮУрГУ для организации работы по изучению курса общей физики.
Курс физики составляет основу теоретической подготовки бакалавров и инженеров и является фундаментальной физико-математической базой, необходимой для успешной деятельности инженера любого профиля.
В результате изучения курса физики студент обязан:
– изучить основные физические явления;
– овладеть понятиями, законами и теориями классической и современной физики;
– овладеть методами физического исследования;
– уметь применять достижения физики в практической деятельности;
– ознакомиться с современной научной аппаратурой;
– приобрести навыки проведения физического эксперимента и умение применять физические законы в прикладных задачах выбранной специальности.
Дисциплина «физика» изучается в течение двух семестров: в 3-м семестре – часть I, в 4-м семестре – часть II. С целью проверки усвоения материала студентами, в каждом семестре применяются следующие виды контроля:
– выполнение двух контрольных работ;
– выполнение лабораторных работ (ЛР) и защита отчетов по ним.
Все виды контроля представлены в табл. 1.
Таблица 1
| № части курса | |||
Виды контроля
Примечание: КР – контрольная работа, СРС – самостоятельная работа студентов, ВЛР – выполнение лабораторных работ.
К экзамену допускаются только студенты, имеющие
1) зачет по ЛР в зачетной книжке,
2) контрольные работы, проверенные и зачтенные.
Студенты ЗИЭФ начинают изучать физику в третьем семестре. Приведем несколько советов по правилам выполнения и оформления контрольных работ (КР) по курсу физики.
С первых дней учебного семестра приступайте к решению задач своей контрольной работы. Необходимый для этого материал представлен на сайте ЗИЭФ по адресу http://zief.susu.ac.ru., а также в учебниках и в учебных пособиях. Сдавать КР необходимо в течение семестра, не позднее одной недели до начала сессии. На титульном листе КР проставляйте номер своего шифра, определяющий номер варианта КР. В конце каждой КР приводите перечень используемой литературы: учебной и методической, – после этого поставьте дату и свою подпись.
Возвращенную не зачтенную КР исправляйте в этой же тетради на оставшихся чистых листах, начиная с заголовка «Работа над ошибками». Отнеситесь к исправлениям серьезно, учитывая все замечания и вопросы, поставленные рецензентом. Обязательно указывайте номер исправленной задачи, не приводя повторно ее текста.
Тетрадь с зачтенной контрольной работой необходимо принести на экзамен.
Часть I
Механические колебания
33. Пружинный маятник жесткостью 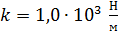 совершает гармонические колебания. Масса груза
совершает гармонические колебания. Масса груза 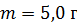 , его максимальная скорость
, его максимальная скорость 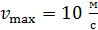 . Определите циклическую частоту
. Определите циклическую частоту 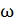 и период колебаний груза
и период колебаний груза 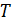 , а также амплитуду колебаний
, а также амплитуду колебаний  .
.
34. Частица массой 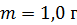 совершает гармонические колебания по закону
совершает гармонические колебания по закону 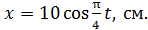 Определите циклическую частоту
Определите циклическую частоту 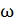 , период колебаний
, период колебаний 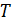 , максимальную скорость частицы
, максимальную скорость частицы 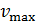 и ее полную механическую энергию
и ее полную механическую энергию 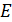 .
.
35. Материальная точка (МТ) массой 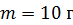 совершает колебания по гармоническому закону
совершает колебания по гармоническому закону 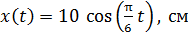 . Определите амплитуду
. Определите амплитуду  и период
и период 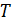 колебаний МТ, а также модуль ее скорости
колебаний МТ, а также модуль ее скорости 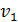 в момент времени
в момент времени 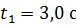 .
.
Термодинамика: цикл Карно
63. Идеальный газ совершает цикл Карно. Температура теплоотдатчика 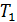 в четыре раза больше температуры теплоприемника
в четыре раза больше температуры теплоприемника 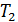 . Определите термический КПД цикла
. Определите термический КПД цикла 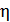 и долю
и долю 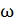 количества теплоты, полученного за один цикл от теплоотдатчика, которую газ отдает теплоприемнику
количества теплоты, полученного за один цикл от теплоотдатчика, которую газ отдает теплоприемнику 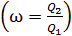 ?
?
64. Определите работу 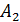 изотермического сжатия газа, совершающего цикл Карно, КПД которого
изотермического сжатия газа, совершающего цикл Карно, КПД которого 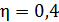 , если работа изотермического расширения газа
, если работа изотермического расширения газа 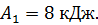
65. Газ, совершающий цикл Карно, отдал теплоприемнику теплоту 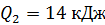 . Определите термический КПД цикла
. Определите термический КПД цикла 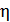 и температуру теплоотдатчика
и температуру теплоотдатчика 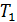 , если при температуре теплоприемника
, если при температуре теплоприемника 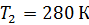 работа газа за цикл
работа газа за цикл 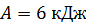 .
.
66. Газ, совершающий цикл Карно, отдал теплоприемнику 67 % теплоты, полученной от теплоотдатчика. Определите термический КПД цикла 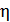 и температуру теплоприемника
и температуру теплоприемника 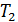 , если температура теплоотдатчика
, если температура теплоотдатчика 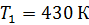 .
.
Конденсаторы
89. Конденсатор емкостью 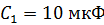 заряжен до напряжения
заряжен до напряжения 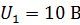 . Определите заряд на обкладках этого конденсатора после того, как параллельно ему подключили незаряженный конденсатор, емкость которого
. Определите заряд на обкладках этого конденсатора после того, как параллельно ему подключили незаряженный конденсатор, емкость которого 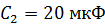 .
.
90. Два конденсатора емкостями 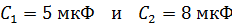 соединены последовательно и подключены к батарее с ЭДС
соединены последовательно и подключены к батарее с ЭДС 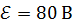 . Определите заряды
. Определите заряды 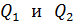 конденсаторов и разности потенциалов
конденсаторов и разности потенциалов 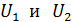 между их обкладками.
между их обкладками.
91. Два заряженных металлических шара, первый радиусом 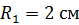 , имеющий заряд
, имеющий заряд 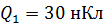 , а второй – радиусом
, а второй – радиусом 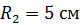 , имеющий потенциал
, имеющий потенциал 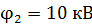 , соединили проводником, емкостью которого можно пренебречь. Определите 1) заряд второго шара до соединения шаров, 2) потенциал шаров
, соединили проводником, емкостью которого можно пренебречь. Определите 1) заряд второго шара до соединения шаров, 2) потенциал шаров 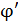 после их соединения, 3) энергии
после их соединения, 3) энергии 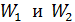 каждого шара до соединения.
каждого шара до соединения.
92. Между обкладками заряженного конденсатора плотно вдвигается пластина диэлектрика с диэлектрической проницаемостью 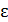 . Сравните емкости конденсатора
. Сравните емкости конденсатора 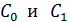 , заряды обкладок
, заряды обкладок 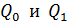 и разности потенциалов между обкладками
и разности потенциалов между обкладками 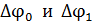 до и после внесения пластины диэлектрика. Рассмотрите два случая: а) конденсатор отключен от источника тока; б) конденсатор подсоединен к источнику тока.
до и после внесения пластины диэлектрика. Рассмотрите два случая: а) конденсатор отключен от источника тока; б) конденсатор подсоединен к источнику тока.
Установочные лекции
Таблица 2
| Номер лекции | Тема занятия | Программные вопросы |
| 1 | Кинематика поступательного и вращательного движения | 1 – 5 |
| 1, 2 | Динамика поступательного и вращательного движения | 6 – 11 |
| 2, 3 | Работа. Энергия. Законы сохранения | 12–17 |
| 3 | Молекулярная физика. Явление переноса | 27, 30–33 |
| 4 | Термодинамика. I и II начала термодинамики. Энтропия. Циклы | 34– 44 |
| 5 | Электрическое поле – напряженность и потенциал. Теорема Остроградского – Гаусса. Работа сил электрического поля | 48–52 |
| 5 | Проводники и диэлектрики в электрическом поле. Электроемкость. Энергия электрического поля | 53–60 |
| 6 | Постоянный электрический ток | 61–65 |
1. 4 . Самостоятельная работа студентов
В самостоятельную работу студентов (СРС) включается следующее:
1) выполнение контрольной работы №1;
2) подготовка к выполнению лабораторных работ (см. раздел 3);
3) подготовка к экзамену (по программным вопросам и задачам);
4) изучение по рекомендуемой литературе тем, представленных в табл. 3.
Таблица 3
| Номер темы | Тема | Программные вопросы |
| 1 | Неинерциальные системы отсчета | 18–19 |
| 2 | Механические колебания | 20–24 |
| 3 | Специальная теория относительности | 25–26 |
| 4 | Распределение молекул по скоростям и в потенциальном силовом поле | 28–29 |
| 5 | Реальный газ | 45–46 |
1.5.Требования к оформлению решения задач контрольной работы
1. Приводите в своей тетради полный текст задачи, а затем краткое условие задачи, выписывая заданные и определяемые величины в общепринятых обозначениях.
2. Внимательно отнеситесь к каждому слову в формулировке задачи, чтобы выделить в ней все, в том числе и неявно заданные величины. Например: «…Найти путь, пройденный телом до остановки». Здесь неявно задана конечная скорость, равная нулю. Или в задаче говорится о газе, находящемся при нормальных условиях. Это означает, что заданы давление 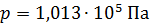 и температура
и температура 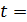 0
0 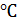 , или
, или 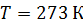 , и т. д.
, и т. д.
3. В решении задачи приводите рисунок, график или схему.
4. Решение задачи сопровождайте краткими, но исчерпывающими пояснениями: а) называйте используемый для решения закон, б) приводите его словесную или математическую формулировку в общем виде, в) объясняйте правомерность применения закона, уточняя формулу закона в условиях данной задачи, г) называйте величины, входящие в формулы, в том числе физические постоянные.
5. Каждую задачу стремитесь решать в общем виде, не делая промежуточных вычислений; решение задачи завершайте расчетной формулой определяемой величины.
6. Вычисляя, в расчетную формулу обязательно подставляйте значения данных и табличных величин, в единицах системы СИ.
Рекомендации к решению физических задач
1. Текст задачи следует внимательно прочитать, чтобы выяснить, какое движение (поступательное, вращательное, качение) или физическое явление рассматривается в задаче. Полезно сделать схематический чертеж или рисунок.
2. На сайте ЗИЭФ (по адресу http://zief.susu.ac.ru.), в разделе 1 – «Теоретическая часть» изучите сведения о явлении, рассматриваемом в задаче: ознакомьтесь с основными формулами и величинами. Выясните, нельзя ли применить законы сохранения (ЗСИ, ЗСМИ, ЗСМЭ) – для этого проверьте, выполняются ли в задаче условия применения закона сохранения (замкнутость механической системы, консервативность сил). Выпишите законы и формулы, которые можно использовать при решении данной задачи.
3. Запишите краткое условие задачи, выбирая для обозначения заданных и искомых величин символы, которые использованы в формулах.
4. Задачу следует решать, как правило, в общем виде, т. е. получить расчетную формулу определяемой величины, содержащую символы заданных величин и физических постоянных.
5. Вычисление определяемой величины начинайте с подстановки в расчетную формулу значений величин. При этом следует помнить, что большинство физических величин имеют свои единицы измерения. Полезно записывать их при подстановке в формулу, чтобы убедиться, что все величины взяты в единицах СИ. Только при вычислении отношений, например, 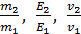 и т. п. можно подставлять величины в любых, но одинаковых единицах, т. е. не обязательно в СИ. Если определяемых величин несколько, то вывод расчетной формулы для следующей начинайте, закончив вычисление предыдущей определяемой величины.
и т. п. можно подставлять величины в любых, но одинаковых единицах, т. е. не обязательно в СИ. Если определяемых величин несколько, то вывод расчетной формулы для следующей начинайте, закончив вычисление предыдущей определяемой величины.
6. Полезно выполнять проверку расчетной формулы на совпадение единиц измерения левой и правой части равенства. Несовпадение единиц указывает на ошибку в расчетной формуле.
7. Вычисления и запись результата делайте с точностью до двух или трех (не более) значащих цифр. Незначащие нули записывайте в виде сомножителя  . При этом, если показатель степени n соответствует приставке, то используйте её: например,
. При этом, если показатель степени n соответствует приставке, то используйте её: например, 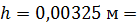
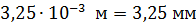 ;
; 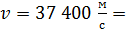 3,74
3,74 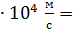 37,4
37,4 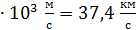 .
.
Примечание: значащими цифрами числа являются все его цифры, кроме нулей, стоящих перед первой, не равной нулю цифрой (значащие цифры могут располагаться как перед, так и после запятой). Приведем примеры чисел, содержащих три значащих цифры: 23,5; 0,0314; 40,0.
8. Помните, что точность результата вычислений не может быть выше, чем точность исходных данных. Это означает, что в полученном результате следует оставить столько значащих цифр, сколько их содержится в наименее точном числе исходных данных задачи.
Рекомендации по выполнению расчетов при решении задач
1. Полученную расчетную формулу проверьте на совпадение единиц измерения искомой величины (в левой и правой части формулы). Это можно сделать как перед вычислениями (в случае получения расчетной формулы долгим путем, в котором велика вероятность появления ошибки), так и непосредственно при подстановке величин в расчетную формулу.
2. Выполняя вычисления, в расчетную формулу подставляйте значения величин с указанием их единиц (независимо от того, была ли сделана предварительная проверка формулы по единицам величин, или нет). Это необходимо делать для того, чтобы убедиться, что все исходные данные взяты в единицах одной системы – системы СИ. При подстановке величин кратные и дольные приставки к единицам (кило-, милли-, нано- и др.) заменяйте соответствующими сомножителями  .
.
3. Отдельно вычислите произведение чисел 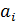 , стоящих перед сомножителями
, стоящих перед сомножителями  , и полученный результат (величину
, и полученный результат (величину 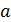 ) сразу (при записи с экрана микрокалькулятора) округлите до 3-х значащих цифр. Затем отдельно вычислите произведение сомножителей
) сразу (при записи с экрана микрокалькулятора) округлите до 3-х значащих цифр. Затем отдельно вычислите произведение сомножителей  . Напомним правила работы с показателями степеней.
. Напомним правила работы с показателями степеней.
При перемножении чисел  показатели степеней складываются (так
показатели степеней складываются (так 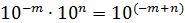 ).
).
При делении чисел показатели вычитаются 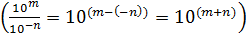 .
.
При возведении числа  в степень показатели степени перемножаются
в степень показатели степени перемножаются 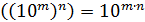 , например,
, например, 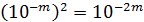 , или
, или 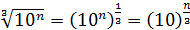 .
.
Замечание: при возведении в дробную степень (например, при извлечении корня), чтобы получить целочисленный показатель степени, следует предварительно сделать показатель степени подкоренного выражения кратным 2 (для квадратного корня) или 3 (в случае кубического корня). Например, 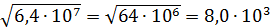 ; или
; или 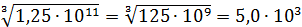 .
.
4. Число, полученное при вычислениях в виде 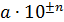 , приведите а) к общепринятому виду, в котором сомножитель
, приведите а) к общепринятому виду, в котором сомножитель 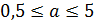 , либо б) к виду, удобному для введения приставки к единице измерения искомой величины. Так
, либо б) к виду, удобному для введения приставки к единице измерения искомой величины. Так 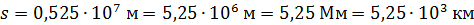 ;
; 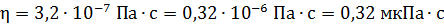 .
.
Приведем примеры.
1. В решении задачи получена расчетная формула для определения момента инерции маховика динамическим методом:
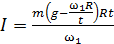 , или
, или 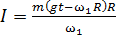 .
.
Проверим формулу по единицам измерения величин:
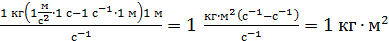 .
.
Получили единицу измерения момента инерции I, следовательно, расчетная формула верна. Вычисляем по ней момент инерции маховика
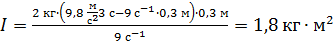 .
.
2. При решении одной из задач получена следующая расчетная формула для высоты 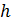 , на которую поднимется поршень в изобарическом процессе расширения газа
, на которую поднимется поршень в изобарическом процессе расширения газа
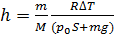 .
.
Вычислим перемещение поршня при нагреве газа по формуле (6):
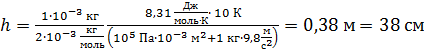 .
.
Примечание:
Результат вычисления записывайте с точностью до двух или трех (не более) значащих цифр. Значащими являются все верные цифры числа, кроме нулей, стоящих перед первой ненулевой цифрой (заметим, что значащие цифры могут быть записаны как до запятой, отделяющей целую часть от дробной, так и после нее). Приведем примеры чисел, содержащих три значащих цифры: 123; 3,45; 0,0216; 20,0 и т. п.
Незначащие нули записывайте в виде сомножителя  . При этом, если показатель степени
. При этом, если показатель степени 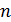 соответствует приставке, то используйте её: например,
соответствует приставке, то используйте её: например, 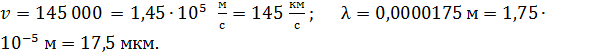 Помните, что точность результата вычислений не может быть выше, чем точность исходных данных: если величины в условии задачи содержат 2 значащие цифры, то в результате вычислений верными будут только 2 значащие цифры (остальные будут ложными и поэтому их не указывают).
Помните, что точность результата вычислений не может быть выше, чем точность исходных данных: если величины в условии задачи содержат 2 значащие цифры, то в результате вычислений верными будут только 2 значащие цифры (остальные будут ложными и поэтому их не указывают).
В случае затруднений при использовании приставок (они указаны в табл. 1 приложения) или при работе с множителями  , постарайтесь усвоить следующие простые правила.
, постарайтесь усвоить следующие простые правила.
Разбивая число 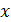 на два сомножителя:
на два сомножителя: 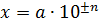 , – величину
, – величину 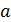 выбирают в интервале (0,5…5,0), при этом показатель степени
выбирают в интервале (0,5…5,0), при этом показатель степени 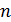 показывает порядок величины числа
показывает порядок величины числа 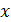 . Если же для искомой физической величины традиционно используют приставки (например, длину волны света
. Если же для искомой физической величины традиционно используют приставки (например, длину волны света 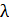 принято выражать в микрометрах (мкм)), то выбирайте значение
принято выражать в микрометрах (мкм)), то выбирайте значение 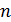 соответствующим ближайшей приставке, которая обычно кратна трем, –
соответствующим ближайшей приставке, которая обычно кратна трем, – 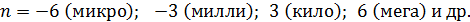
Если при таком пересчете множитель  пришлось уменьшить в 10 раз, то необходимо увеличить в 10 раз второй сомножитель –
пришлось уменьшить в 10 раз, то необходимо увеличить в 10 раз второй сомножитель – 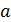 , чтобы число
, чтобы число 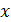 не изменилось; и наоборот: увеличивая множитель
не изменилось; и наоборот: увеличивая множитель  , например, в 100 раз, уменьшайте в 100 раз сомножитель
, например, в 100 раз, уменьшайте в 100 раз сомножитель 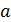 .
.
Приведем примеры: 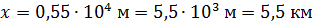 ;
; 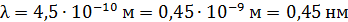 . Запись величины
. Запись величины 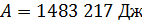 является неграмотной, так как показывает, что величина работы
является неграмотной, так как показывает, что величина работы  определена с точностью до 7 значащих цифр; не менее ошибочна и запись этой величины в виде
определена с точностью до 7 значащих цифр; не менее ошибочна и запись этой величины в виде 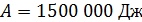 , так как округление величины не уменьшило число значащих цифр (5 нулей являются значащими). Правильной является запись
, так как округление величины не уменьшило число значащих цифр (5 нулей являются значащими). Правильной является запись 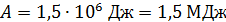 (если в исходных данных две значащих цифры), либо
(если в исходных данных две значащих цифры), либо 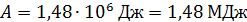 , если при вычислении величины
, если при вычислении величины  использовали данные с тремя значащими цифрами.
использовали данные с тремя значащими цифрами.
Приведем пример решения и оформления задачи при выполнении контрольной работы.
1.8. Пример решения и оформления задачи контрольной работы
Задача 102. Материальная точка вращается вокруг неподвижной оси по закону 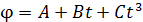 , где
, где 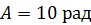 ,
, 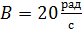 ,
, 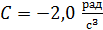 . Определите полное ускорение точки, находящейся на расстоянии
. Определите полное ускорение точки, находящейся на расстоянии 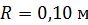 от оси вращения, для момента времени
от оси вращения, для момента времени 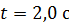 .
.
Дано
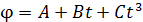 ; ;
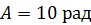 ; ;
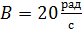 ; ;
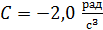 ; ;
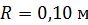 ; ;
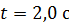 . .
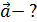
| ||
Решение
Вращающаяся точка движется по окружности; при этом ее полное ускорение 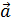 равно сумме векторов ускорений – тангенциального
равно сумме векторов ускорений – тангенциального 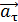 , направленного по касательной к траектории, и нормального ускорения
, направленного по касательной к траектории, и нормального ускорения 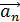 , направленного к центру кривизны траектории:
, направленного к центру кривизны траектории:
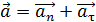 .
.
Так как векторы 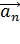 и
и 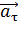 взаимно перпендикулярны, то модуль ускорения
взаимно перпендикулярны, то модуль ускорения
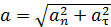 . (1)
. (1)
Линейные ускорения материальной точки: нормальное и тангенциальное, – связаны с угловыми величинами следующими формулами:
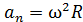 ;
; 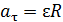 , (2)
, (2)
где 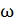 – угловая скорость точки;
– угловая скорость точки; 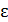 – ее угловое ускорение.
– ее угловое ускорение.
Подставляя выражения (2) в формулу (1), получаем расчетную формулу в виде:
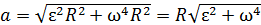 . (3)
. (3)
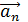
|
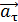
|
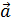
|
Угловую скорость 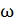 находим, как первую производную от угла поворота по времени:
находим, как первую производную от угла поворота по времени:
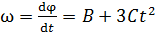 .
.
В момент времени 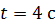 модуль угловой скорости
модуль угловой скорости
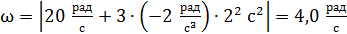 .
.
Угловое ускорение равно первой производной от угловой скорости по времени:
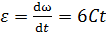 .
.
Его модуль в момент времени 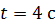 :
:
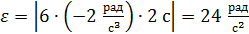 .
.
Подставляя значения 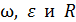 в формулу (3) вычисляем линейное ускорение материальной точки:
в формулу (3) вычисляем линейное ускорение материальной точки:
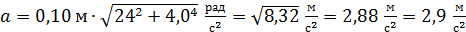 .
.
Библиографический список
1. Трофимова, Т.И. Курс физики: учебное пособие для инженерно-технических специальностей вузов / Т.И. Трофимова. – М.: Академия, 2010. – 557 с.
2. Писарев, Н.М. Физика: Курс лекций для студентов инженерных специальностей вузов / Н.М. Писарев; под ред. Г.П. Вяткина. – Челябинск: Изд-во ЧГТУ, 1997. – Ч.1. – 171 с. Ч.2. – 299 с.
3. Детлаф, А.А. Курс физики: учебное пособие для втузов / А.А. Детлаф, Б.М. Яворский. – М.: Академия, 2008. – 719 с.
4. Савельев, И.В. Курс физики Т.1: Механика. Т.2: Электричество и магнетизм. Т.3: Молекулярная физика: учебное пособие для втузов: в 5 т. / И.В. Савельев. – СПб. и др.: Лань, 2011. – 342 с.
5. Савельев, И.В. Курс физики Т.3: Молекулярная физика: учебное пособие для втузов: в 5 т. / И.В. Савельев. – СПб. и др.: Лань, 2008. – 208 с.
6. Механика и молекулярная физика. Руководство к решению задач: учебное пособие для студентов вузов / В.К. Герасимов, Т.О. Миронова, Ю.Б. Пейсахов, Т.П. Привалова. – Челябинск: Издательский центр ЮУрГУ, 2014. – 83 с. http://physics.susu.ac.ru/data/ mechanics.pdf.
7. Чертов, А.Г. Задачник по физике: учебное пособие для втузов / А.Г. Чертов, А.А. Воробьев. – М.: Издательство Физматлит, 2008. – 640 с.
8. Иродов, И.Е. Задачи по общей физике: учебное пособие для втузов / И.Е. Иродов. – СПб. и др.: Лань, 2009. – 431 с.
9. Фирганг, Е.В. Руководство к решению задач по курсу общей физики: учебное пособие для втузов по техническим и технологическим направлениям / Е.В. Фирганг. – СПб. и др.: Лань, 2009. – 347 с.
10. Механика и молекулярная физика: учебное пособие к выполнению лабораторных работ / В.К. Герасимов, А.Е. Гришкевич, С.И. Морозов и др.; под ред. В.П. Бескачко. – Челябинск: Изд-во ЮУрГУ, 2008. – 95 с.
11. Механика и молекулярная физика: учебное пособие к выполнению лабораторных работ / В.К. Герасимов, А.Е. Гришкевич, С.И. Морозов и др.; под ред. В.П. Бескачко. – Челябинск: Изд-во ЮУрГУ, 2008. – 95 с. http://physics.susu.ac.ru/data/mechanics.pdf.
12. Герасимов, В.К. Физика. Т.1: Механика и молекулярная физика. Учебное пособие по физике: выполнение контрольных и лабораторных работ; в 3 т. / В.К. Герасимов, Т.О. Миронова, Ю.Б. Пейсахов, Т.П. Привалова. – 125 с. Сайт ЗИЭФ ЮУрГУ – http://zief.susu.ac.ru.
13. Герасимов, В.К. Физика. Т.2: Электромагнетизм. Учебное пособие по физике: выполнение контрольных и лабораторных работ; в 3 т. / В.К. Герасимов, Т.О. Миронова, Ю.Б. Пейсахов, Т.П. Привалова. – 140 с. Сайт ЗИЭФ ЮУрГУ – http://zief.susu.ac.ru.
КОНТРОЛЬНАЯ РАБОТА № 1
Студент ЗИЭФ решает 6 задач своего варианта, номер которого совпадает с последней цифрой его шифра. Номера задач каждого варианта представлены в табл. 4.
2.1. Таблица вариантов контрольной работы № 1
Таблица 4
| Вариант | Номера задач | |||||
| 0 | 110 | 120 | 130 | 140 | 150 | 160 |
| 1 | 101 | 111 | 121 | 131 | 141 | 151 |
| 2 | 102 | 112 | 122 | 132 | 142 | 152 |
| 3 | 103 | 113 | 123 | 133 | 143 | 153 |
| 4 | 104 | 114 | 124 | 134 | 144 | 154 |
| 5 | 105 | 115 | 125 | 135 | 145 | 155 |
| 6 | 106 | 116 | 126 | 136 | 146 | 156 |
| 7 | 107 | 117 | 127 | 137 | 147 | 157 |
| 8 | 108 | 118 | 128 | 138 | 148 | 158 |
| 9 | 109 | 119 | 129 | 139 | 149 | 159 |
Построение графиков
Назначение графика – наглядно представить результаты опыта при изучении зависимости одной величины от другой. График позволяет увидеть особенности исследуемой зависимости, выявить ее характер (линейная, квадратичная или экспоненциальная) и определить параметры. Все это становится доступным при грамотном применении графического метода, а для этого необходимо следовать определенным правилам построения графиков и использовать методы их обработки.
1. Выбор координатных осей. График выполняют на листе миллиметровой бумаги размером 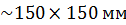 ; координатные оси берут примерно равной длины. Горизонтальная ось отводится аргументу, т. е. величине, значение которой задает сам экспериментатор, а вертикальная ось – функции. В конце каждой оси указывают символ величины, десятичный множитель и единицу величины. При этом десятичный множитель
; координатные оси берут примерно равной длины. Горизонтальная ось отводится аргументу, т. е. величине, значение которой задает сам экспериментатор, а вертикальная ось – функции. В конце каждой оси указывают символ величины, десятичный множитель и единицу величины. При этом десятичный множитель 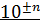 позволяет опустить нули при нанесении шкалы, например, писать 1; 2; 3 ... вместо 0,001; 0,002 и т.д.
позволяет опустить нули при нанесении шкалы, например, писать 1; 2; 3 ... вместо 0,001; 0,002 и т.д.
2. Выбор интервалов. Интервалы чисел на каждой оси выбирают независимо друг от друга, причем такие, чтобы кривая заняла все поле чертежа. Для этого границы интервалов берут близкими к наименьшему и наибольшему среди измеренных значений. Подчеркнем, что начало отсчета часто начинают не с нуля. Нулевую точку помещают на график лишь в том случае, если она близка к экспериментально исследованной области или необходима экстраполяция на нулевое значение.
3. Выбор масштабов и шкалы. Масштаб должен быть простым и удобным для нанесения точек на график. За единицу масштаба принимают отрезок оси, кратный 5, 10, 50 или 100 мм, что позволяет легко отсчитывать доли отрезка. Такому отрезку соотносят "круглое" число (1, 2, 5) единиц измеряемой величины. Деления шкалы на каждой оси подбирают независимо, в соответствии с масштабом, причем надписи делений наносят вдоль всей оси. Чтобы шкала легко читалась, достаточно указать на оси 3–5 чисел.
4. Нанесение точек. Опытные данные наносят на поле графика в виде четких значков, не подписывая их численные значения – они приводятся только в таблице. Разные значки (светлые и темные кружки, треугольники и др.) используют для обозначения данных, относящихся к различным условиям.
5. Проведение экспериментальной кривой. Кривую проводят плавной, непрерывной линией (таковы обычно физические зависимости) так, чтобы точки находились равномерно по обе стороны кривой как можно ближе к ней. Если вид зависимости известен заранее, то проводят эту теоретическую кривую.
Для линейной зависимости: прямую проводят через среднюю точку, координаты которой определяют по следующим формулам:
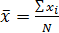 ;
; 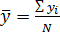 .
.
Здесь записаны суммы 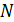 слагаемых измеренных величин;
слагаемых измеренных величин; 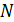 – общее число точек на графике.
– общее число точек на графике.
6. Заголовок графика. График сопровождают названием зависимости, в котором называют символы величин, указанные в конце осей. Кроме того, в подписи к графику разъясняют обозначения опытных точек и кривых, если их несколько. Заголовок принято располагать выше графика, либо под графиком.
Приближенный метод
Пусть измеренные величины 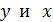 связаны линейной зависимостью вида
связаны линейной зависимостью вида 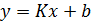 и требуется определить ее параметры
и требуется определить ее параметры 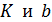 .
.
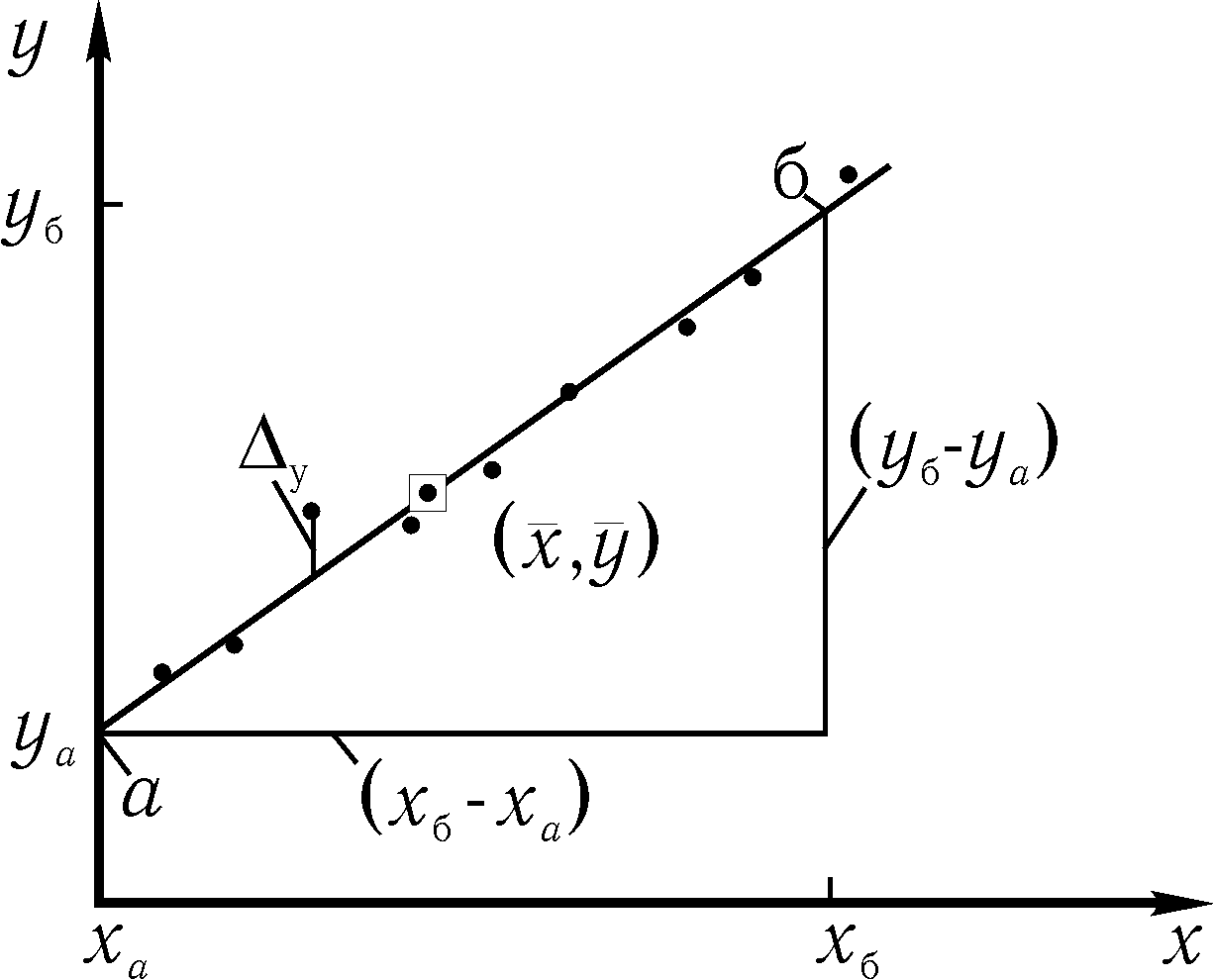 Рис. 4. Определение параметров
Рис. 4. Определение параметров 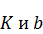
|
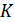 , удобно точку а взять на одной из осей, а точку б – так, чтобы отрезок
, удобно точку а взять на одной из осей, а точку б – так, чтобы отрезок 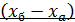 выражался целым числом.
выражался целым числом.
Среднее значение углового коэффициента 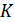 вычисляют как отношение, определяющее наклон прямой:
вычисляют как отношение, определяющее наклон прямой:
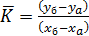 .
.
Параметр b линейной зависимости находят по графику как ординату точки пересечения прямой с осью 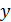 . Величину
. Величину 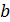 можно найти и по уравнению прямой, подставляя координаты средней точки графика:
можно найти и по уравнению прямой, подставляя координаты средней точки графика:
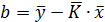 .
.
Случайные погрешности параметров определяются разбросом опытных точек по отношению к проведенной прямой. Для простейшей оценки этих погрешностей достаточно найти на графике величину 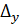 – отклонение наиболее удаленной точки от прямой линии, и
– отклонение наиболее удаленной точки от прямой линии, и 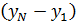 – интервал, в котором сделаны измерения (длина оси
– интервал, в котором сделаны измерения (длина оси 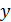 ).
).
Абсолютная случайная погрешность параметра b: 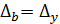 .
.
Для углового коэффициента прямой линии 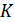 сначала вычисляют относительную погрешность:
сначала вычисляют относительную погрешность:
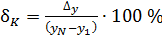 .
.
Эта формула привлекает тем, что при расчете отношения величин одного рода можно взять их в любых единицах (всего удобнее – в малых делениях шкалы оси 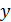 ). Напомним, что в величине погрешности имеет значение, как правило, одна цифра, а потому достаточная точность отсчета отрезка
). Напомним, что в величине погрешности имеет значение, как правило, одна цифра, а потому достаточная точность отсчета отрезка 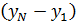 – "круглое число", например, 90, 100 или 120 мм (или 10 – 15 клеток масштабной бумаги).
– "круглое число", например, 90, 100 или 120 мм (или 10 – 15 клеток масштабной бумаги).
Затем находят абсолютную погрешность средней величины 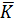 :
:
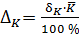 ,
,
чтобы записать доверительный интервал для искомого параметра 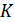 :
:
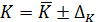 .
.
Доверительная вероятность 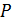 в описанном методе оценки погрешностей (по максимальному отклонению
в описанном методе оценки погрешностей (по максимальному отклонению 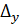 ) зависит от числа опытных точек
) зависит от числа опытных точек 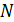 – чем больше число
– чем больше число 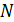 , тем выше надежность результата:
, тем выше надежность результата:
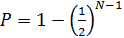 .
.
Темы лабораторных работ
Таблица 5
| Название работы | Номер работы в учебном пособии |
| 1. Изучение динамики вращательного движения | 3 |
| 2. Определение ускорения свободного падения с помощью оборотного и математического маятников | 7 |
| 3. Определение отношения теплоемкостей воздуха | 12 |
Подготовка к выполнению лабораторных работ
Методические указания к выполнению лабораторных работ: описание метода измерений, лабораторного стенда, порядок выполнения ЛР и обработки результатов измерений, – содержатся в следующем учебном пособии:
Механика и молекулярная физика: учебное пособие к выполнению лабораторных работ / В.К. Герасимов, А.Е. Гришкевич, С.И. Морозов и др.; под ред. В.П. Бескачко. – Челябинск: Изд-во ЮУрГУ, 2008. – 95 с.
Данное учебное пособие можно найти по следующему электронному адресу: http :// physics . susu . ac . ru / data / mechanics . pdf .
При подготовке к занятию в лаборатории настоятельно рекомендуем по каждой выполняемой ЛР заполнить некоторые разделы бланка отчета (до таблиц опытных данных): цель работы, описание установки и метода измерений (включая название величин, входящих в расчетные формулы). Это позволит Вам получить представление о лабораторной работе и, благодаря этому, избежать ненужных ошибок при проведении эксперимента в физической лаборатории.
Перед выполнением лабораторных работ необходимо изучить раздел 3.1 «Введение в лабораторный практикум по физике» (с. 40-47) – п. п. 3.1.1. Проведение лабораторного эксперимента и 3.1.2. Графическое представление и обработка результатов измерений.
3.3.1. Рекомендации к выполнению лабораторных работ
ИЗУЧЕНИЕ ЗАКОНА ДИНАМИКИ
ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА
Bыполнил(а)_______________
гр. _________ “_____”__________20___г.
Проверил _________________
“______”________20___г.
ЦЕЛЬ РАБОТЫ:
СХЕМА УСТАНОВКИ
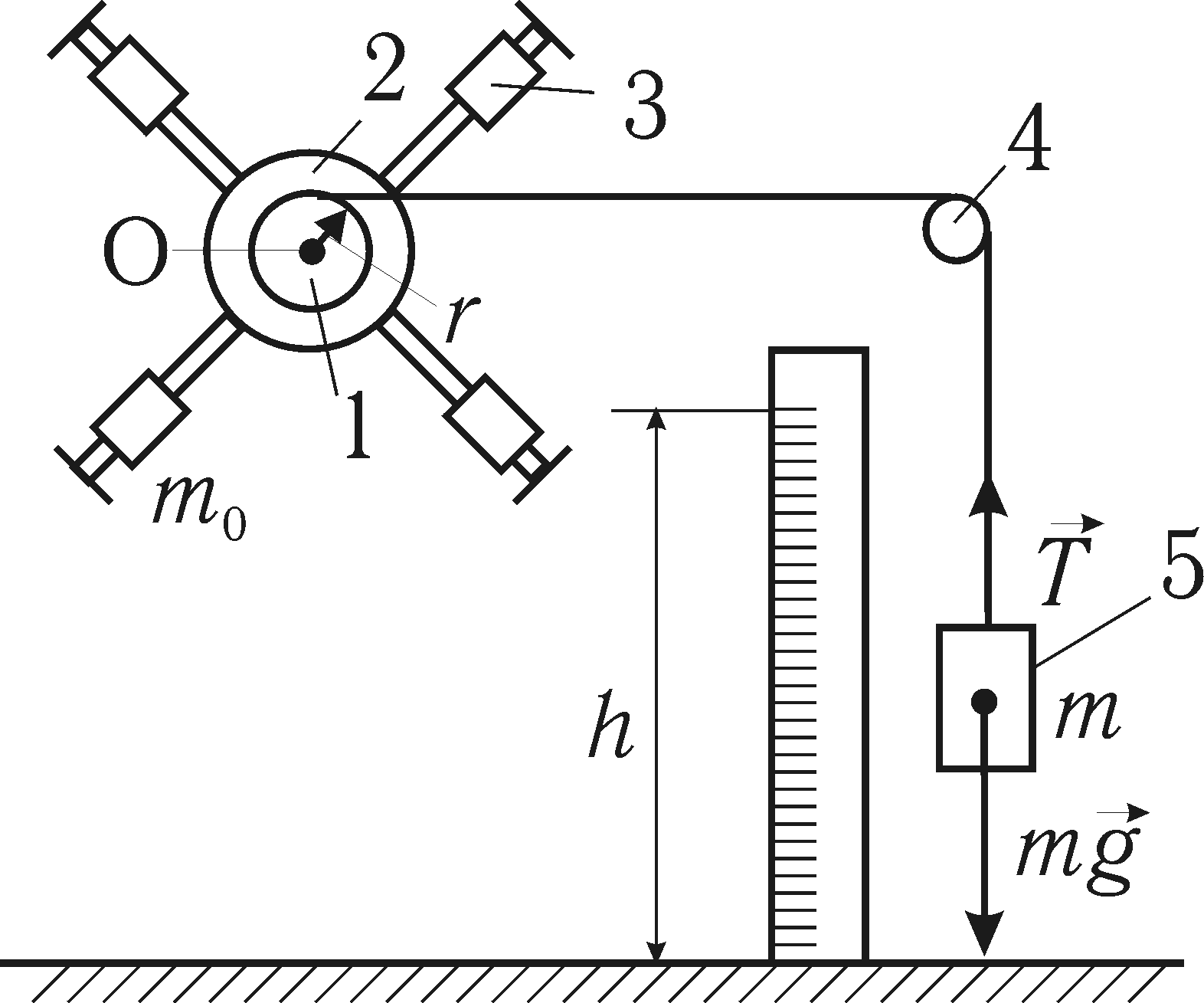
| 1 и 2 – 3 – 4 – 5 – |
Ускорение, с которым падает груз: 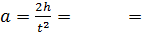
Угловое ускорение вращающегося маятника: 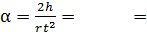
Момент силы, действующий на маятник: 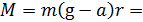
Закон динамики для маятника Обербека: 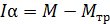 ,
,
где 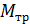 – момент сил трения.
– момент сил трения.
Задание 1. Изучение закона вращения маятника
ОПЫТНЫЕ ДАННЫЕ
Таблица 1
|
| |||||
| № | 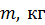
| 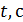
| 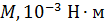
| 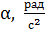 , ,
|
| 1 | |||||
| 2 | |||||
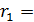
| 3 | ||||
| 4 | |||||
| 5 | |||||
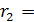
| 6 | ||||
| 7 | |||||
| 8 | |||||
| Координаты средней точки (для графика) | |||||
Зависимость углового ускорения маятника 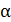 от момента сил
от момента сил 
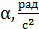 ;
;
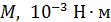
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ
Расчет момента инерции (по графику 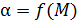 )
)
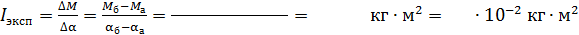 .
.
ВЫВОД
Задание 2. Исследование зависимости момента инерции от распределения
массы относительно оси вращения
ОПЫТНЫЕ ДАННЫЕ
Таблица 2
| | ||||
| № |
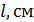
| 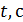
|
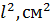
|
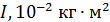
|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| Координаты средней точки (для графика) | ||||
Расчет момента инерции для построения графика 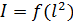 :
:

Зависимость момента инерции маятника 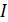
от квадрата расстояния 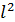 от оси вращения до грузов
от оси вращения до грузов
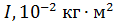
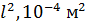
Определяем по графику 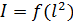 :
:
Момент инерции крестовины 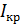
(путем экстраполяции опытной прямой линии до расстояния 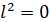 ):
):
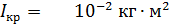 .
.
Масса подвижных грузов 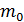
(по угловому коэффициенту 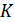 опытной прямой линии:
опытной прямой линии: 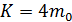 ):
):
 .
.
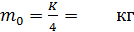 .
.
ВЫВОД
Южно-Уральский государственный университет
Оптика. Интерференция света
57. Плосковыпуклая стеклянная линза с радиусом кривизны 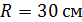 лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете
лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете 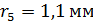 . Определите длину световой волны
. Определите длину световой волны 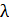 .
.
58. Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом с длиной волны 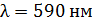 . Определите толщину воздушного промежутка
. Определите толщину воздушного промежутка 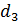 в том месте, где в отраженном свете наблюдается третье светлое кольцо.
в том месте, где в отраженном свете наблюдается третье светлое кольцо.
59. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой с радиусом кривизны 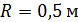 находится некоторая жидкость. При наблюдении в отраженном свете с длиной волны
находится некоторая жидкость. При наблюдении в отраженном свете с длиной волны 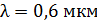 измерен радиус третьего темного кольца Ньютона:
измерен радиус третьего темного кольца Ньютона: 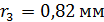 . Определите показатель преломления
. Определите показатель преломления 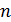 жидкости.
жидкости.
60. На тонкую пленку по нормали к ее поверхности падает монохроматический свет с длиной волны 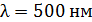 . Отраженный от пленки свет максимально усилен вследствие интерференции. Определите минимальную толщину пленки
. Отраженный от пленки свет максимально усилен вследствие интерференции. Определите минимальную толщину пленки 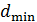 , если показатель преломления материала пленки
, если показатель преломления материала пленки 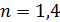 .
.
61. В опыте Юнга расстояние от щелей до экрана 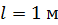 ; длина волны света
; длина волны света  . Определите расстояние
. Определите расстояние 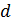 между щелями, если на участке экрана длиной
между щелями, если на участке экрана длиной 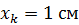 укладывается
укладывается 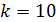 темных интерференционных полос.
темных интерференционных полос.
62. На стеклянную линзу объектива с показателем преломления 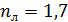 нанесена тонкая прозрачная пленка вещества с показателем преломления
нанесена тонкая прозрачная пленка вещества с показателем преломления 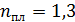 . Объектив освещен падающим на него нормально пучком света с длиной волны
. Объектив освещен падающим на него нормально пучком света с длиной волны 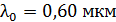 . Определите наименьшую толщину пленки
. Определите наименьшую толщину пленки 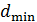 , при которой отраженный свет будет иметь минимальную интенсивность.
, при которой отраженный свет будет иметь минимальную интенсивность.
63. На тонкий стеклянный клин с показателем преломления 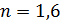 падает нормально параллельный пучок света с длиной волны
падает нормально параллельный пучок света с длиной волны 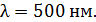 Расстояние между соседними темными интерференционными полосами в отраженном свете
Расстояние между соседними темными интерференционными полосами в отраженном свете 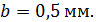 Определите угол
Определите угол 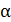 между поверхностями клина.
между поверхностями клина.
Поляризация света
71. Пластинку кварца толщиной 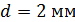 поместили между параллельными николями, в результате чего плоскость поляризации монохроматического света повернулась на угол
поместили между параллельными николями, в результате чего плоскость поляризации монохроматического света повернулась на угол 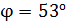 . Какой наименьшей толщины
. Какой наименьшей толщины 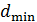 следует взять пластинку, чтобы поле зрения поляриметра стало совершенно темным?
следует взять пластинку, чтобы поле зрения поляриметра стало совершенно темным?
72. Кварцевую пластинку поместили между скрещенными николями. При какой наименьшей толщине кварцевой пластинки 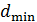 поле зрения между николями будет максимально просветлено? Постоянная вращения кварца
поле зрения между николями будет максимально просветлено? Постоянная вращения кварца 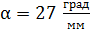 .
.
73. При прохождении света в трубке длиной 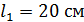 , содержащей раствор сахара концентрацией
, содержащей раствор сахара концентрацией 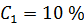 , плоскость поляризации света повернулась на угол
, плоскость поляризации света повернулась на угол 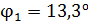 . В другом растворе сахара в трубке длиной
. В другом растворе сахара в трубке длиной 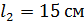 плоскость поляризации света повернулась на угол
плоскость поляризации света повернулась на угол 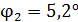 . Определите концентрацию
. Определите концентрацию 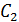 второго раствора.
второго раствора.
74. Луч естественного света проходит последовательно через два поляроида, угол между плоскостями пропускания которых 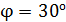 . Принимая, что коэффициент поглощения света в каждом поляроиде
. Принимая, что коэффициент поглощения света в каждом поляроиде 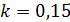 , определите, во сколько раз уменьшится интенсивность света, выходящего из второго поляроида, по сравнению с интенсивностью луча, падающего на первый.
, определите, во сколько раз уменьшится интенсивность света, выходящего из второго поляроида, по сравнению с интенсивностью луча, падающего на первый.
75. Угол падения луча на поверхность стекла 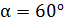 . При этом отраженный луч света максимально поляризован. Определите угол преломления луча
. При этом отраженный луч света максимально поляризован. Определите угол преломления луча 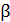 .
.
76. Луч света переходит из жидкости в стекло. Угол падения луча 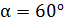 , угол преломления
, угол преломления 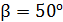 . Определите угол падения светового луча
. Определите угол падения светового луча 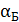 , при котором свет, отраженный от границы раздела этих сред, будет полностью поляризован.
, при котором свет, отраженный от границы раздела этих сред, будет полностью поляризован.
Тепловое излучение
77. Вычислите истинную температуру 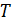 раскаленной вольфрамовой ленты, если радиационный пирометр показывает температуру
раскаленной вольфрамовой ленты, если радиационный пирометр показывает температуру 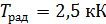 . Считайте, что поглощательная способность вольфрама
. Считайте, что поглощательная способность вольфрама 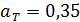 и не зависит от длины волны излучения.
и не зависит от длины волны излучения.
78. Температура абсолютно черного тела 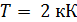 . Определите длину волны
. Определите длину волны 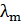 , на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости
, на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости 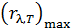 для этой длины волны.
для этой длины волны.
79. Определите температуру 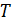 и энергетическую светимость
и энергетическую светимость 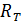 абсолютно черного тела, если максимум энергии излучения приходится на длину волны
абсолютно черного тела, если максимум энергии излучения приходится на длину волны 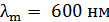 .
.
80. Из смотрового окна печи излучается поток энергии 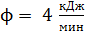 . Определите температуру
. Определите температуру 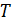 печи, если площадь окна
печи, если площадь окна 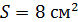 .
.
81. Как и во сколько раз изменится поток излучения 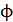 абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра:
абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра: 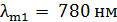 , на фиолетовую границу –
, на фиолетовую границу – 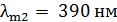 ?
?
82. Муфельная печь, потребляющая мощность 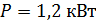 , имеет отверстие площадью
, имеет отверстие площадью 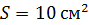 . Определите долю
. Определите долю 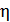 мощности, которая рассеивается стенками печи, если температура ее внутренней поверхности
мощности, которая рассеивается стенками печи, если температура ее внутренней поверхности 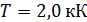 .
.
Фотоэлектрический эффект
83. Красная граница фотоэффекта для цинка 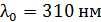 . Определите максимальную кинетическую энергию фотоэлектронов
. Определите максимальную кинетическую энергию фотоэлектронов 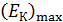 в джоулях и в электрон-вольтах, если на фотокатод падает свет с длиной волны
в джоулях и в электрон-вольтах, если на фотокатод падает свет с длиной волны 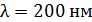 .
.
84. На поверхность калия падает свет с длиной волны 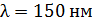 . Определите максимальную кинетическую энергию фотоэлектронов
. Определите максимальную кинетическую энергию фотоэлектронов 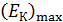 .
.
85. Фотон с энергией 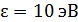 падает на серебряную пластинку и вызывает фотоэффект. Определите импульс
падает на серебряную пластинку и вызывает фотоэффект. Определите импульс 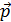 , полученный пластинкой, принимая, что скорости движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластинки.
, полученный пластинкой, принимая, что скорости движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластинки.
86. На фотоэлемент с катодом из лития падает свет с длиной волны 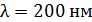 . Определите наименьшее значение задерживающей разности потенциалов
. Определите наименьшее значение задерживающей разности потенциалов 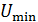 , которую нужно приложить к фотоэлементу, чтобы фототок стал равен нулю.
, которую нужно приложить к фотоэлементу, чтобы фототок стал равен нулю.
87. Какова должна быть длина волны 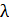 рентгеновского излучения, падающего на платиновую пластинку, чтобы максимальная скорость фотоэлектронов
рентгеновского излучения, падающего на платиновую пластинку, чтобы максимальная скорость фотоэлектронов 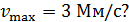
88. На металлический фотокатод направлен пучок ультрафиолетового излучения с длиной волны 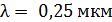 . Фототок прекращается, если приложить минимальную задерживающую разность потенциалов
. Фототок прекращается, если приложить минимальную задерживающую разность потенциалов 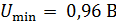 . Определите работу выхода
. Определите работу выхода  электронов из металла.
электронов из металла.
Фотон. Давление света
89. Для фотона рентгеновского излучения с длиной волны 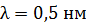 найдите энергию
найдите энергию 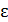 (в джоулях и электрон-вольтах), массу
(в джоулях и электрон-вольтах), массу 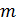 и импульс
и импульс 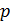 .
.
90. Определите энергетическую освещенность 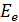 зеркальной поверхности, если давление, оказываемое излучением,
зеркальной поверхности, если давление, оказываемое излучением, 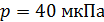 . Излучение падает по нормали к поверхности.
. Излучение падает по нормали к поверхности.
91. Свет падает по нормали на зеркальную поверхность, находящуюся на расстоянии 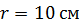 от точечного изотропного излучателя. При какой мощности излучателя
от точечного изотропного излучателя. При какой мощности излучателя 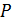 давление света на поверхность
давление света на поверхность 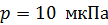 ?
?
92. На черную поверхность площадью 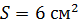 падает по нормали поток излучения
падает по нормали поток излучения 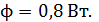 Определите давление
Определите давление 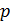 и силу давления излучения
и силу давления излучения 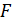 на эту поверхность.
на эту поверхность.
93. Давление излучения с длиной волны 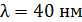 , падающего нормально на черную поверхность,
, падающего нормально на черную поверхность, 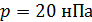 . Определите число фотонов
. Определите число фотонов 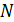 , падающих за время
, падающих за время 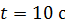 на площадь
на площадь 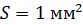 этой поверхности.
этой поверхности.
Эффект Комптона
94. Рентгеновское излучение с длиной волны 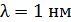 рассеивается на практически свободных электронах. Определите максимальную длину волны
рассеивается на практически свободных электронах. Определите максимальную длину волны 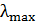 рентгеновского излучения в рассеянном пучке.
рентгеновского излучения в рассеянном пучке.
95. Фотон с длиной волны 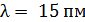 рассеялся на свободном электроне. Длина волны рассеянного фотона
рассеялся на свободном электроне. Длина волны рассеянного фотона 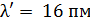 . Определите угол рассеяния
. Определите угол рассеяния 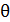 .
.
96. В эффекте Комптона фотон с энергией 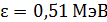 рассеялся на свободном электроне на угол
рассеялся на свободном электроне на угол 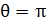 . Определите кинетическую энергию
. Определите кинетическую энергию 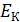 электрона отдачи.
электрона отдачи.
Атомная физика. Теория Бора
97. Для электрона, находящегося на второй орбите ( 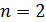 ) атома водорода, определите радиус орбиты
) атома водорода, определите радиус орбиты 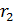 , момент импульса электрона
, момент импульса электрона 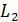 , а также направление и величину его скорости
, а также направление и величину его скорости 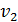 .
.
98. Для электрона, находящегося на первой орбите ( 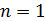 ) атома водорода, определите радиус орбиты
) атома водорода, определите радиус орбиты 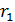 , скорость электрона на этой орбите
, скорость электрона на этой орбите 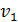 (направление и величину) и период обращения электрона
(направление и величину) и период обращения электрона 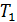 .
.
99. Для атома водорода определите 1) полную энергию электрона 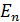 на орбитах с главным квантовым числом
на орбитах с главным квантовым числом 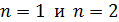 и 2) длину волны λ фотона, излучаемого при переходе электрона со второго энергетического уровня на первый – в серии Лаймана (ультрафиолетовой).
и 2) длину волны λ фотона, излучаемого при переходе электрона со второго энергетического уровня на первый – в серии Лаймана (ультрафиолетовой).
100. Для атома водорода определите 1) полную энергию электрона 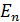 на орбитах с главным квантовым числом
на орбитах с главным квантовым числом 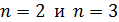 и 2) длину волны λ фотона, излучаемого при переходе электрона с третьего энергетического уровня на второй – в серии Бальмера (видимой).
и 2) длину волны λ фотона, излучаемого при переходе электрона с третьего энергетического уровня на второй – в серии Бальмера (видимой).
101. Для атома водорода определите 1) полную энергию электрона 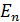 на орбитах с главным квантовым числом
на орбитах с главным квантовым числом 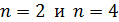 и 2) длину волны λ фотона, излучаемого при переходе электрона с четвертого энергетического уровня на второй – в серии Бальмера (видимой).
и 2) длину волны λ фотона, излучаемого при переходе электрона с четвертого энергетического уровня на второй – в серии Бальмера (видимой).
102. Для атома водорода определите 1) полную энергию электрона 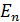 на орбитах с главным квантовым числом
на орбитах с главным квантовым числом 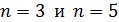 и 2) длину волны λ фотона, излучаемого при переходе электрона с пятого энергетического уровня на третий – в серии Пашена (в инфракрасной области).
и 2) длину волны λ фотона, излучаемого при переходе электрона с пятого энергетического уровня на третий – в серии Пашена (в инфракрасной области).
Элементы квантовой механики
103. Электрон движется со скоростью 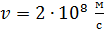 . Определите длину волны де Бройля
. Определите длину волны де Бройля 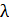 электрона, учитывая зависимость его массы от скорости.
электрона, учитывая зависимость его массы от скорости.
104. Какую ускоряющую разность потенциалов 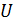 прошел электрон, если его длина волны де Бройля: а)
прошел электрон, если его длина волны де Бройля: а) 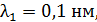 б)
б) 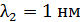 ?
?
105. Параллельный пучок атомов водорода, падающий под углом скольжения 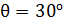 к поверхности монокристалла, дает дифракционный максимум 1-го порядка при отражении от плоскостей с межатомным расстоянием
к поверхности монокристалла, дает дифракционный максимум 1-го порядка при отражении от плоскостей с межатомным расстоянием 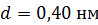 . Определите длину волны де Бройля
. Определите длину волны де Бройля 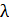 атомов водорода и их скорость
атомов водорода и их скорость 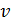 .
.
106. Определите длину волны де Бройля 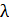 протона, прошедшего ускоряющую разность потенциалов: а)
протона, прошедшего ускоряющую разность потенциалов: а) 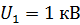 , б)
, б) 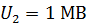 .
.
107. Определите длину волны де Бройля 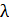 атома гелия (
атома гелия ( 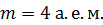 ), имеющего скорость: а)
), имеющего скорость: а) 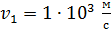 , б)
, б) 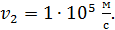
108. Электрон, имеющий кинетическую энергию 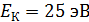 , находится в металлической пылинке диаметром
, находится в металлической пылинке диаметром 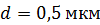 . Оцените относительную точность
. Оцените относительную точность 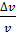 , с которой можно определить скорость электрона
, с которой можно определить скорость электрона 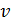 .
.
109. Используя соотношение неопределенностей, оцените наименьшие погрешности 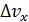 в определении скоростей электрона и протона, если координаты этих частиц установлены с неопределенностью
в определении скоростей электрона и протона, если координаты этих частиц установлены с неопределенностью 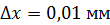 .
.
110. Используя соотношение неопределенностей 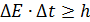 , оцените ширину энергетического уровня атома водорода, находящегося: 1) в основном состоянии –
, оцените ширину энергетического уровня атома водорода, находящегося: 1) в основном состоянии – 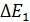 ; 2) в возбужденном состоянии –
; 2) в возбужденном состоянии – 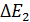 , в котором время жизни атома
, в котором время жизни атома 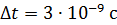 .
.
111. Время жизни возбужденного атома 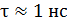 . С какой наименьшей погрешностью
. С какой наименьшей погрешностью 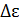 может быть определена энергия фотона, излучаемого атомом.
может быть определена энергия фотона, излучаемого атомом.
112. Оцените неопределенность скорости 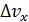 электрона в основном состоянии атома водорода, принимая, что неопределенность координаты электрона
электрона в основном состоянии атома водорода, принимая, что неопределенность координаты электрона 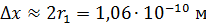 .
.
Установочные лекции
Таблица 6
| Номер лекции | Тема и содержание лекции | Програм-мные вопросы |
| 1 | Магнитное поле. Закон Био – Савара – Лапласа. Закон Ампера. Закон полного тока. Магнитный поток. Работа в магнитном поле. Сила Лоренца. Магнетики | 1–12 |
| 2 | Явление электромагнитной индукции. Самоиндукция. Энергия магнитного поля. Свободные электрические колебания | 13–18 |
| 3 | Интерференция, дифракция и поляризация света | 26-42 |
| 4 | Тепловое излучение. Фотоэффект, эффект Комптона. Давление света | 44–54 |
| 5 | Строение атома. Оптические спектры. Постулаты Бора. Рентгеновские спектры. Закон Мозли | 55–60 |
| 6 | Элементы квантовой механики и атомной физики | 61–70 |
4.4. Самостоятельная работа студентов
В самостоятельную работу студентов (СРС) включается следующее:
1) выполнение двух контрольных работ;
2) подготовка к выполнению лабораторных работ (см. раздел 7);
3) подготовка к экзамену (по программным вопросам);
4) изучение по рекомендуемой литературе тем, представленных в табл. 7.
Таблица 7
| Номер темы | Тема работы | Програм-мные вопросы |
| 1 | Затухающие и вынужденные электрические колебания | 19-20 |
| 2 | Электромагнитное поле. Ток смещения. Уравнения Максвелла. Электромагнитные волны. Свойства и шкала ЭМВ | 21-23 |
| 3 | Голография | 37–38 |
| 4 | Лазеры | 65 |
| 5 | Атомная энергетика: ядерные реакции деления и синтеза | 71–72 |
Библиографический список
1. Трофимова, Т.И. Курс физики: учебное пособие для инженерно-технических специальностей вузов / Т.И. Трофимова. – М.: Академия, 2010. – 557 с.
2. Писарев, Н.М. Физика: Курс лекций для студентов инженерных специальностей вузов / Н.М. Писарев; под ред. Г.П. Вяткина. – Челябинск: Изд-во ЧГТУ, 1997. – Ч.2. – 299 с.
3. Детлаф, А.А. Курс физики: учебное пособие для втузов / А.А. Детлаф, Б.М. Яворский. – М.: Академия, 2008. – 719 с.
4. Савельев, И.В. Курс физики Т.2: Электричество и магнетизм: учебное пособие для втузов: в 5 т. / И.В. Савельев. – СПб. и др.: Лань, 2011. – 342 с.
5. Савельев, И.В. Курс физики Т.4: Волны. Оптика: учебное пособие для втузов: в 5 т. / И.В. Савельев. – СПб. и др.: Лань, 2011. – 251 с.
6. Савельев, И.В. Курс физики Т.5: Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц: учебное пособие для втузов: в 5 т. / И.В. Савельев. – СПб. и др.: Лань, 2011. – 384 с.
7. Чертов, А.Г. Задачник по физике: учебное пособие для втузов / А.Г. Чертов, А.А. Воробьев. – М.: Издательство Физматлит, 2008. – 640 с.
8. Фирганг, Е.В. Руководство к решению задач по курсу общей физики: учебное пособие для втузов по техническим направлениям и специальностям / Е.В. Фирганг. – СПб. и др.: Лань, 2009. – 347 с.
9. Герасимов, В.К. Электричество и магнетизм. Руководство к реше-нию задач: учебное пособие для студентов вузов / В.К. Герасимов, Т.О. Миронова, Ю.Б. Пейсахов, Т.П. Привалова.– Челябинск: Издатель-ский центр ЮУрГУ, 2014. – 140 с.
10. Герасимов, В.К. Физика. Руководство по изучению курса физики: учебное пособие для студентов вузов заочной формы обучения / В.К. Герасимов, Т.О. Миронова, Ю.Б. Пейсахов, Т.П. Привалова. – Челябинск: Издательский центр ЮУрГУ, 2015. – 146 с.
11. Электричество и магнетизм: учебное пособие к выполнению лабораторных работ по курсу физики / Л.Ф. Гладкова, А.Е. Гришкевич, С.И. Морозов и др.; под ред. А.Е. Гришкевича. – Челябинск: Изд-во ЮУрГУ, 2009. – 110 с.
КОНТРОЛЬНАЯ РАБОТА № 2
Студент решает 6 задач своего варианта, номер которого совпадает с последней цифрой шифра. Номера задач каждого варианта представлены в табл. 8.
| Вариант | Номера задач | |||||
| 0 | 210 | 220 | 230 | 240 | 250 | 260 |
| 1 | 201 | 211 | 221 | 231 | 241 | 251 |
| 2 | 202 | 212 | 222 | 232 | 242 | 252 |
| 3 | 203 | 213 | 223 | 233 | 243 | 253 |
| 4 | 204 | 214 | 224 | 234 | 244 | 254 |
| 5 | 205 | 215 | 225 | 235 | 245 | 255 |
| 6 | 206 | 216 | 226 | 236 | 246 | 256 |
| 7 | 207 | 217 | 227 | 237 | 247 | 257 |
| 8 | 208 | 218 | 228 | 238 | 248 | 258 |
| 9 | 209 | 219 | 229 | 239 | 249 | 259 |
5.1. Таблица вариантов контрольной работы № 2
Таблица 8
Рекомендации к решению задач по разделу «Электромагнетизм»
1. Внимательно прочитайте условие задачи. Выясните, какое явление рассматривается в задаче, и изучите сведения о нем и о физических величинах, его описывающих, по учебному пособию.
2. При определении магнитных сил, магнитного потока и других величин обратите внимание на то, какое магнитное поле рассматривается в задаче – однородное или неоднородное. В первом случае используйте более простые формулы для однородного МП.
3. При решении задачи определяйте направления искомых векторов 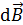 ,
, 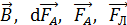 и др. Для этого используйте а) определительные формулы, в правой части которых записано векторное произведение векторов или б) правило буравчика и правило левой руки.
и др. Для этого используйте а) определительные формулы, в правой части которых записано векторное произведение векторов или б) правило буравчика и правило левой руки.
4. В том случае, если магнитное поле создается в ферромагнетике, для которого магнитная проницаемость 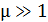 (в отличие от картонного или воздушного сердечника, имеющего
(в отличие от картонного или воздушного сердечника, имеющего 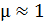 ), необходимо определять величину
), необходимо определять величину 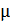 по формуле, связывающей напряженность
по формуле, связывающей напряженность 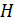 и магнитную индукцию
и магнитную индукцию 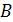 :
:
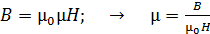 .
.
При этом следует учесть, что величина магнитной индукции зависит от напряженности МП: 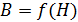 , – и соответственно
, – и соответственно 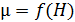 . Поэтому сначала вычисляют напряженность магнитного поля
. Поэтому сначала вычисляют напряженность магнитного поля 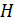 , которая зависит только от тока в контуре и формы и размеров контура (катушки). Затем по экспериментальному графику кривой намагничивания
, которая зависит только от тока в контуре и формы и размеров контура (катушки). Затем по экспериментальному графику кривой намагничивания 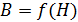 для заданного материала сердечника (используя справочные данные) по рассчитанной величине
для заданного материала сердечника (используя справочные данные) по рассчитанной величине 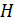 определяют индукцию магнитного поля
определяют индукцию магнитного поля 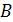 . По найденным значениям
. По найденным значениям 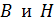 вычисляют магнитную проницаемость сердечника по записанной выше формуле.
вычисляют магнитную проницаемость сердечника по записанной выше формуле.
В магнитном поле
221. Плоский контур площадью 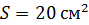 находится в однородном магнитном поле с индукцией
находится в однородном магнитном поле с индукцией 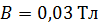 . Определите магнитный поток
. Определите магнитный поток 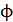 , пронизывающий контур, если его плоскость составляет угол
, пронизывающий контур, если его плоскость составляет угол 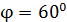 с направлением линий магнитной индукции.
с направлением линий магнитной индукции.
222. Магнитный поток сквозь сечение соленоида 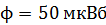 . Длина соленоида
. Длина соленоида 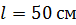 . Определите магнитный момент
. Определите магнитный момент 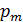 соленоида, если его витки плотно прилегают друг к другу.
соленоида, если его витки плотно прилегают друг к другу.
223. В средней части соленоида, содержащего 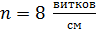 , помещен круговой виток диаметром
, помещен круговой виток диаметром 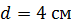 . Плоскость витка расположена под углом
. Плоскость витка расположена под углом 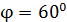 к оси соленоида. Определите магнитный поток
к оси соленоида. Определите магнитный поток 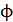 , пронизывающий виток, если по обмотке соленоида течет ток
, пронизывающий виток, если по обмотке соленоида течет ток 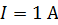 .
.
224. На длинный цилиндрический каркас радиусом 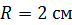 уложена «виток к витку» однослойная обмотка из проволоки диаметром
уложена «виток к витку» однослойная обмотка из проволоки диаметром 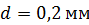 . Определите магнитный поток
. Определите магнитный поток 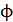 , создаваемый таким соленоидом при силе тока
, создаваемый таким соленоидом при силе тока 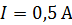 .
.
225. Плоский контур с током 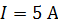 свободно установился в однородном магнитном поле с индукцией
свободно установился в однородном магнитном поле с индукцией 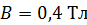 . Площадь контура
. Площадь контура 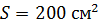 . Поддерживая ток в контуре неизменным, его повернули относительно оси, лежащей в плоскости контура, на угол
. Поддерживая ток в контуре неизменным, его повернули относительно оси, лежащей в плоскости контура, на угол 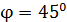 . Определите совершенную при этом работу
. Определите совершенную при этом работу  .
.
226. Квадратный контур со стороной 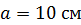 , в котором течет ток
, в котором течет ток 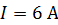 , находится в магнитном поле с индукцией
, находится в магнитном поле с индукцией 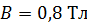 ; плоскость контура расположена под углом
; плоскость контура расположена под углом 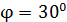 к линиям магнитной индукции. Какую работу
к линиям магнитной индукции. Какую работу  нужно совершить, чтобы при неизменной силе тока в контуре изменить его форму на окружность?
нужно совершить, чтобы при неизменной силе тока в контуре изменить его форму на окружность?
227. Виток, в котором поддерживается постоянная сила тока 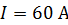 , свободно установился в однородном магнитном поле с индукцией
, свободно установился в однородном магнитном поле с индукцией 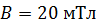 . Радиус витка
. Радиус витка 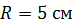 . Какую работу
. Какую работу  нужно совершить для того, чтобы повернуть виток относительно оси, совпадающей с его диаметром, на угол
нужно совершить для того, чтобы повернуть виток относительно оси, совпадающей с его диаметром, на угол 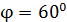 .
.
228. В однородном магнитном поле перпендикулярно линиям индукции расположен плоский контур площадью 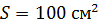 . Поддерживая в контуре постоянную силу тока
. Поддерживая в контуре постоянную силу тока 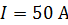 , его переместили в область пространства, где поле отсутствует. Определите магнитную индукцию поля
, его переместили в область пространства, где поле отсутствует. Определите магнитную индукцию поля 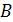 , если при перемещении контура была совершена работа
, если при перемещении контура была совершена работа 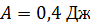 .
.
229. Плоский круговой контур радиусом 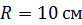 с током
с током 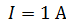 расположен в однородном магнитном поле с индукцией
расположен в однородном магнитном поле с индукцией 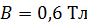 так, что нормаль к контуру перпендикулярна линиям магнитной индукции. Определите работу
так, что нормаль к контуру перпендикулярна линиям магнитной индукции. Определите работу  , совершаемую силами поля при медленном повороте контура вокруг оси, лежащей в плоскости контура, на угол
, совершаемую силами поля при медленном повороте контура вокруг оси, лежащей в плоскости контура, на угол 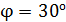 .
.
230. Определите магнитный поток 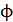 , пронизывающий соленоид, если его длина
, пронизывающий соленоид, если его длина 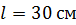 и магнитный момент
и магнитный момент 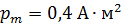 .
.
Энергия магнитного поля
231. В однородном магнитном поле с индукцией 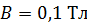 равномерно с частотой
равномерно с частотой 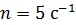 вращается проводящий стержень длиной
вращается проводящий стержень длиной 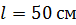 так, что плоскость его вращения перпендикулярна линиям магнитной индукции, а ось вращения проходит через конец стержня. Определите разность потенциалов
так, что плоскость его вращения перпендикулярна линиям магнитной индукции, а ось вращения проходит через конец стержня. Определите разность потенциалов 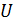 , индуцируемую на концах стержня.
, индуцируемую на концах стержня.
232. В однородном магнитном поле с индукцией 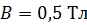 вращается с частотой
вращается с частотой 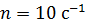 проводящий стержень длиной
проводящий стержень длиной 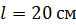 . Плоскость его вращения перпендикулярна линиям магнитной индукции, а ось вращения проходит через конец стержня. Определите разность потенциалов
. Плоскость его вращения перпендикулярна линиям магнитной индукции, а ось вращения проходит через конец стержня. Определите разность потенциалов 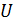 , индуцируемую на концах стержня.
, индуцируемую на концах стержня.
233. В проволочное кольцо, присоединенное к интегратору тока, вставили прямой магнит. При этом по цепи прошел заряд 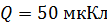 . Покажите на схеме цепи направление индукционного тока в кольце и определите изменение магнитного потока
. Покажите на схеме цепи направление индукционного тока в кольце и определите изменение магнитного потока 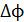 через плоскость кольца, если сопротивление цепи
через плоскость кольца, если сопротивление цепи 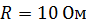 .
.
234. Замкнутый медный провод массой 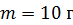 , имеющий форму квадрата, помещен в однородное магнитное поле с индукцией
, имеющий форму квадрата, помещен в однородное магнитное поле с индукцией 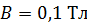 так, что плоскость контура перпендикулярна линиям поля. Покажите на схеме направление индукционного тока в контуре и определите заряд
так, что плоскость контура перпендикулярна линиям поля. Покажите на схеме направление индукционного тока в контуре и определите заряд 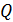 , который потечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию.
, который потечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию.
235. Рамка из провода сопротивлением 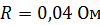 равномерно вращается в однородном магнитном поле с индукцией
равномерно вращается в однородном магнитном поле с индукцией 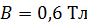 . Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Площадь рамки
. Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Площадь рамки 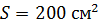 . Покажите направление индукционного тока в рамке и определите заряд
. Покажите направление индукционного тока в рамке и определите заряд 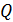 , который потечет по рамке при изменении угла между нормалью к рамке и линиями индукции от 0 до
, который потечет по рамке при изменении угла между нормалью к рамке и линиями индукции от 0 до 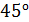 .
.
236. Проволочный виток диаметром 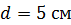 и сопротивлением
и сопротивлением 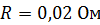 находится в однородном магнитном поле с индукцией
находится в однородном магнитном поле с индукцией 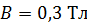 . Плоскость витка составляет угол
. Плоскость витка составляет угол 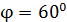 с линиями индукции. Какой заряд
с линиями индукции. Какой заряд 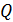 протечет по витку при выключении магнитного поля? Покажите направление индукционного тока в витке.
протечет по витку при выключении магнитного поля? Покажите направление индукционного тока в витке.
237. Рамка, содержащая 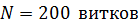 тонкого провода, может свободно вращаться вокруг оси, лежащей в плоскости рамки. Площадь рамки
тонкого провода, может свободно вращаться вокруг оси, лежащей в плоскости рамки. Площадь рамки 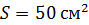 . Ось вращения рамки перпендикулярна линиям однородного магнитного поля с индукцией
. Ось вращения рамки перпендикулярна линиям однородного магнитного поля с индукцией 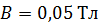 . Определите максимальную ЭДС
. Определите максимальную ЭДС 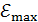 , которая индуцируется в рамке при ее вращении с частотой
, которая индуцируется в рамке при ее вращении с частотой 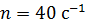 .
.
238. Прямой проводящий стержень длиной 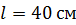 находится в однородном магнитном поле с индукцией
находится в однородном магнитном поле с индукцией 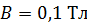 . Концы стержня замкнуты проводом, находящимся вне поля. Сопротивление цепи
. Концы стержня замкнуты проводом, находящимся вне поля. Сопротивление цепи 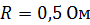 . Какая мощность
. Какая мощность 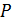 требуется для равномерного движения стержня со скоростью
требуется для равномерного движения стержня со скоростью 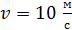 , перпендикулярной линиям магнитной индукции?
, перпендикулярной линиям магнитной индукции?
239. Проволочный контур площадью 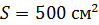 и сопротивлением
и сопротивлением 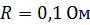 равномерно вращается в однородном магнитном поле с индукцией
равномерно вращается в однородном магнитном поле с индукцией 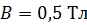 . Ось вращения лежит в плоскости контура и перпендикулярна линиям магнитной индукции. Определите максимальную мощность
. Ось вращения лежит в плоскости контура и перпендикулярна линиям магнитной индукции. Определите максимальную мощность 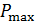 , необходимую для вращения контура с угловой скоростью
, необходимую для вращения контура с угловой скоростью 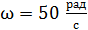 .
.
240. Кольцо из медного провода массой 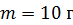 помещено в однородное магнитное поле с индукцией
помещено в однородное магнитное поле с индукцией 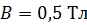 ; плоскость кольца составляет угол
; плоскость кольца составляет угол 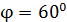 с линиями магнитной индукции. Покажите направление индукционного тока и определите заряд
с линиями магнитной индукции. Покажите направление индукционного тока и определите заряд 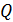 , который пройдет по кольцу, если снять магнитное поле.
, который пройдет по кольцу, если снять магнитное поле.
241. Соленоид сечением 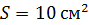 содержит
содержит 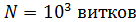 . При силе тока
. При силе тока 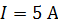 магнитная индукция поля внутри соленоида
магнитная индукция поля внутри соленоида 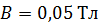 . Определите индуктивность
. Определите индуктивность 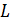 соленоида и энергию его магнитного поля
соленоида и энергию его магнитного поля 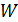 .
.
242. На картонный каркас радиусом 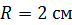 и длиной
и длиной 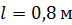 намотан в один слой провод диаметром
намотан в один слой провод диаметром 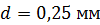 так, что витки плотно прилегают друг к другу. Вычислите индуктивность
так, что витки плотно прилегают друг к другу. Вычислите индуктивность 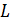 полученного соленоида.
полученного соленоида.
243. Катушка, намотанная на цилиндрический каркас, имеет 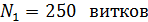 и индуктивность
и индуктивность 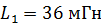 . Чтобы увеличить индуктивность катушки до
. Чтобы увеличить индуктивность катушки до 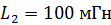 , обмотку катушки заменили обмоткой из более тонкого провода с таким расчетом, чтобы длина катушки
, обмотку катушки заменили обмоткой из более тонкого провода с таким расчетом, чтобы длина катушки 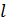 осталась прежней. Какое число витков
осталась прежней. Какое число витков 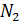 оказалось в катушке после перемотки?
оказалось в катушке после перемотки?
244. Индуктивность соленоида с однослойной обмоткой 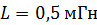 . Длина соленоида
. Длина соленоида 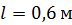 , радиус
, радиус 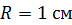 . Определите отношение числа витков соленоида к его длине:
. Определите отношение числа витков соленоида к его длине: 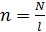 .
.
245. Обмотка соленоида содержит 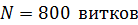 . Сердечник из немагнитного материала имеет сечение
. Сердечник из немагнитного материала имеет сечение 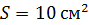 . По обмотке течет ток, создающий поле с магнитной индукцией
. По обмотке течет ток, создающий поле с магнитной индукцией 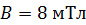 . Определите среднее значение ЭДС самоиндукции
. Определите среднее значение ЭДС самоиндукции 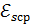 , которая появится на зажимах соленоида, если сила тока уменьшится практически до нуля за время
, которая появится на зажимах соленоида, если сила тока уменьшится практически до нуля за время 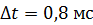 .
.
246. По катушке индуктивностью 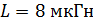 течет ток
течет ток 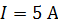 . Определите среднее значение ЭДС самоиндукции
. Определите среднее значение ЭДС самоиндукции 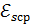 , возникающей в контуре, при уменьшении силы тока практически до нуля за время
, возникающей в контуре, при уменьшении силы тока практически до нуля за время 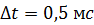 .
.
247. В электрической цепи, содержащей резистор сопротивлением 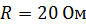 и катушку индуктивностью
и катушку индуктивностью 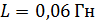 , течет ток
, течет ток 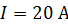 . Определите направление и величину индукционного тока I в цепи через время
. Определите направление и величину индукционного тока I в цепи через время 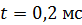 после отключения источника тока без разрывания цепи.
после отключения источника тока без разрывания цепи.
248. Цепь состоит из катушки индуктивностью 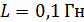 и источника тока. Источник отключили, не разрывая цепи. За время
и источника тока. Источник отключили, не разрывая цепи. За время 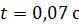 сила тока уменьшилась до
сила тока уменьшилась до 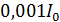 , где
, где 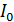 – начальное значение. Определите активное сопротивление катушки
– начальное значение. Определите активное сопротивление катушки 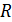 .
.
249. Источник тока замкнули на катушку сопротивлением 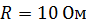 и индуктивностью
и индуктивностью 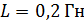 . За какое время
. За какое время 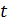 ток в цепи достигнет величины, равной
ток в цепи достигнет величины, равной 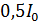 , где
, где 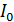 – установившееся значение? Покажите направление индукционного тока в катушке.
– установившееся значение? Покажите направление индукционного тока в катушке.
250. Источник тока замкнули на катушку сопротивлением 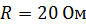 . За время
. За время 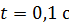 , прошедшее от момента замыкания, сила тока в катушке достигла
, прошедшее от момента замыкания, сила тока в катушке достигла 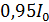 , где
, где 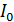 – установившееся значение. Покажите направление индукционного тока в катушке и определите индуктивность катушки
– установившееся значение. Покажите направление индукционного тока в катушке и определите индуктивность катушки 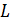 .
.
КОНТРОЛЬНАЯ РАБОТА № 3
Студент решает 6 задач своего варианта, номер которого совпадает с последней цифрой шифра. Номера задач каждого варианта представлены в табл. 9.
6.1. Таблица вариантов контрольной работы № 3
Таблица 9
| Вариант | Номера задач | |||||
| 0 | 310 | 320 | 330 | 340 | 350 | 360 |
| 1 | 301 | 311 | 321 | 331 | 341 | 351 |
| 2 | 302 | 312 | 322 | 332 | 342 | 352 |
| 3 | 303 | 313 | 323 | 333 | 343 | 353 |
| 4 | 304 | 314 | 324 | 334 | 344 | 354 |
| 5 | 305 | 315 | 325 | 335 | 345 | 355 |
| 6 | 306 | 316 | 326 | 336 | 346 | 356 |
| 7 | 307 | 317 | 327 | 337 | 347 | 357 |
| 8 | 308 | 318 | 328 | 338 | 348 | 358 |
| 9 | 309 | 319 | 329 | 339 | 349 | 359 |
Рекомендации к решению задач по разделу «Оптика»
1. Текст задачи следует внимательно прочитать, чтобы выяснить, какое физическое явление рассматривается в задаче. Полезно изобразить схематический чертеж или рисунок.
2. Ознакомьтесь с основными формулами для данного явления. Выясните, можно ли применить законы сохранения (ЗСИ, ЗСЗ, ЗСЭ) – для этого проверьте, выполняются ли в задаче условия применения закона. Выпишите законы и формулы, пригодные для решения данной задачи.
3. Запишите краткое условие задачи, выбирая для обозначения данных и искомых величин символы, которые будут использованы в формулах.
4. Задачу следует решать, как правило, в общем виде, чтобы получить расчетную формулу определяемой величины, содержащую символы заданных величин и физических постоянных.
5. Вычисление определяемой величины начинайте с подстановки в расчетную формулу значений величин. При этом следует помнить, что большинство физических величин имеют свои единицы измерения. Полезно записывать их при подстановке в формулу, чтобы убедиться, что все величины взяты в единицах СИ. Только при вычислении отношений, например,  и т. п. можно подставлять значения величин в любых, но одинаковых единицах, т. е. не обязательно в СИ. Если определяемых величин несколько, то вывод расчетной формулы для следующей величины начинайте, закончив вычисление предыдущей.
и т. п. можно подставлять значения величин в любых, но одинаковых единицах, т. е. не обязательно в СИ. Если определяемых величин несколько, то вывод расчетной формулы для следующей величины начинайте, закончив вычисление предыдущей.
6. Полезно выполнять проверку расчетной формулы на совпадение единиц измерения левой и правой части равенства. Несовпадение единиц указывает на ошибку в расчетной формуле.
7. Вычисление и запись результата делайте с точностью до двух или трех (не более) значащих цифр. Незначащие нули записывайте в виде сомножителя  . При этом, если показатель степени n соответствует приставке, используйте её: например,
. При этом, если показатель степени n соответствует приставке, используйте её: например, 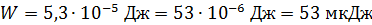 ;
; 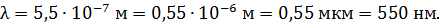 Помните, что точность результата вычислений не может быть выше, чем точность исходных данных. Рекомендации по выполнению расчетов при решении задач подробно изложены в п. 1.7 (см. с. 27-29).
Помните, что точность результата вычислений не может быть выше, чем точность исходных данных. Рекомендации по выполнению расчетов при решении задач подробно изложены в п. 1.7 (см. с. 27-29).
8. Оцените разумность полученного значения искомой величины одним из следующих путей: а) по физическому смыслу; б) сравнением с табличным значением или, по порядку величины, с числами, приведенными в рекомендациях к решению задач по данной теме.
Рекомендации к решению задач по разделу
«Атомная и ядерная физика»
1. В стационарных состояниях атома параметры электрона: радиус круговой орбиты, скорость электрона и его момент импульса, период обращения, энергия электрона, – имеют дискретные значения, которые определяются главным квантовым числом 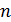 (номер орбиты). Эта зависимость отражается индексом величин:
(номер орбиты). Эта зависимость отражается индексом величин: 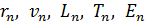 .
.
2. По мере увеличения номера орбиты 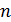 ее радиус увеличивается
ее радиус увеличивается 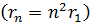 , а скорость электрона уменьшается
, а скорость электрона уменьшается 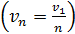 ; в результате период обращения растет
; в результате период обращения растет 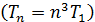 , возрастает момент импульса электрона
, возрастает момент импульса электрона 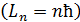 и увеличивается его энергия
и увеличивается его энергия 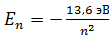 .
.
3. Порядок величин параметров электрона в атоме водорода можно оценить по указанным зависимостям и значениям величин для основного состояния 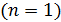 . В этом состоянии радиус орбиты
. В этом состоянии радиус орбиты 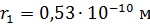 , скорость электрона
, скорость электрона 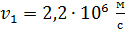 , период обращения
, период обращения 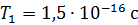 , момент импульса
, момент импульса 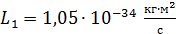 , и полная энергия электрона
, и полная энергия электрона 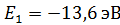 .
.
4. Рекомендации по выполнению расчетов при решении задач подробно изложены в п. 1.7 (см. стр. 27-29).
Интерференция света
301. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой с радиусом кривизны 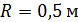 находится некоторая жидкость. При наблюдении в отраженном свете с длиной волны
находится некоторая жидкость. При наблюдении в отраженном свете с длиной волны 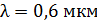 измерен радиус третьего темного кольца Ньютона:
измерен радиус третьего темного кольца Ньютона: 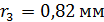 . Определите показатель преломления
. Определите показатель преломления 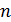 жидкости.
жидкости.
302. На тонкую пленку по нормали к ее поверхности падает монохроматический свет с длиной волны 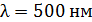 . Отраженный от пленки свет максимально усилен вследствие интерференции. Определите минимальную толщину пленки
. Отраженный от пленки свет максимально усилен вследствие интерференции. Определите минимальную толщину пленки 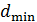 , если показатель преломления материала пленки
, если показатель преломления материала пленки 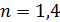 .
.
303. В опыте Юнга расстояние от щелей до экрана 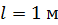 ; длина волны света
; длина волны света  . Определите расстояние
. Определите расстояние 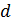 между щелями, если на участке экрана длиной
между щелями, если на участке экрана длиной 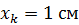 укладывается
укладывается 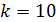 темных интерференционных полос.
темных интерференционных полос.
304. На стеклянную пластинку положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена монохроматическим светом с длиной волны 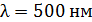 . Определите радиус линзы
. Определите радиус линзы 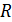 , если радиус четвертого темного кольца Ньютона в отраженном свете
, если радиус четвертого темного кольца Ньютона в отраженном свете 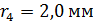 .
.
305. На тонкую глицериновую пленку с показателем преломления 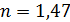 и толщиной
и толщиной 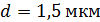 падает белый свет по нормали к поверхности пленки. Определите длины волн
падает белый свет по нормали к поверхности пленки. Определите длины волн 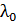 лучей видимого участка спектра (
лучей видимого участка спектра ( 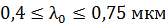 ), которые в отраженном свете будут ослаблены в результате интерференции.
), которые в отраженном свете будут ослаблены в результате интерференции.
306. На стеклянную линзу объектива с показателем преломления 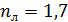 нанесена тонкая прозрачная пленка вещества с показателем преломления
нанесена тонкая прозрачная пленка вещества с показателем преломления 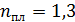 . Объектив освещен падающим на него нормально пучком света с длиной волны
. Объектив освещен падающим на него нормально пучком света с длиной волны 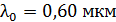 . Определите наименьшую толщину пленки
. Определите наименьшую толщину пленки 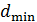 , при которой отраженный свет будет иметь минимальную интенсивность.
, при которой отраженный свет будет иметь минимальную интенсивность.
307. На тонкий стеклянный клин с показателем преломления 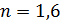 падает нормально параллельный пучок света с длиной волны
падает нормально параллельный пучок света с длиной волны 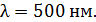 Расстояние между соседними темными интерференционными полосами в отраженном свете
Расстояние между соседними темными интерференционными полосами в отраженном свете 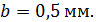 Определите угол
Определите угол 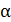 между поверхностями клина.
между поверхностями клина.
308. Плосковыпуклая стеклянная линза с радиусом кривизны 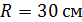 лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете
лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете 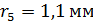 . Определите длину световой волны
. Определите длину световой волны 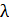 .
.
309. Между двумя плоскопараллельными пластинками на расстоянии 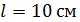 от линии их соприкосновения находится проволока диаметром
от линии их соприкосновения находится проволока диаметром 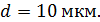 Пластинки, образующие воздушный клин, освещаются нормально падающим монохроматическим светом с длиной волны
Пластинки, образующие воздушный клин, освещаются нормально падающим монохроматическим светом с длиной волны 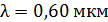 . Определите ширину
. Определите ширину 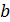 интерференционных полос, наблюдаемых в отраженном свете.
интерференционных полос, наблюдаемых в отраженном свете.
310. Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом с длиной волны 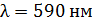 . Определите толщину воздушного промежутка
. Определите толщину воздушного промежутка 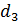 в том месте, где в отраженном свете наблюдается третье светлое кольцо.
в том месте, где в отраженном свете наблюдается третье светлое кольцо.
Дифракция света
311. Какое наименьшее число щелей 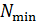 должна содержать дифракционная решетка, чтобы в спектре второго порядка можно было видеть раздельно две желтые линии натрия с длинами волн
должна содержать дифракционная решетка, чтобы в спектре второго порядка можно было видеть раздельно две желтые линии натрия с длинами волн 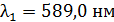 и
и 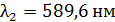 ? Определите длину
? Определите длину 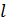 такой решетки, если постоянная решетки
такой решетки, если постоянная решетки 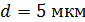 ?
?
312. На поверхность дифракционной решетки по нормали падает монохроматический свет. Постоянная дифракционной решетки 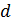 в 4
в 4 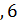 раза больше, чем длина световой волны
раза больше, чем длина световой волны 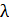 . Определите общее число
. Определите общее число 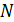 дифракционных максимумов, которые теоретически можно наблюдать в данном случае.
дифракционных максимумов, которые теоретически можно наблюдать в данном случае.
313. На дифракционную решетку по нормали к ней падает параллельный пучок белого света. Спектры третьего и четвертого порядка частично накладываются друг на друга. Определите длину волны 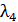 спектральной линии в спектре четвертого порядка, на которую накладывается линия границы спектра третьего порядка:
спектральной линии в спектре четвертого порядка, на которую накладывается линия границы спектра третьего порядка: 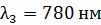 ?
?
314. На дифракционную решетку, содержащую 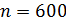 штрихов на одном миллиметре длины, падает нормально белый свет. Линзой, помещенной вблизи решетки, дифракционный спектр проецируется на экран. Определите длину
штрихов на одном миллиметре длины, падает нормально белый свет. Линзой, помещенной вблизи решетки, дифракционный спектр проецируется на экран. Определите длину 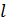 спектра первого порядка на экране, если расстояние от линзы до экрана
спектра первого порядка на экране, если расстояние от линзы до экрана 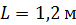 . Длины волн границ видимого спектра:
. Длины волн границ видимого спектра: 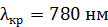 ,
, 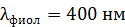 .
.
315. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения. Расстояние между атомными плоскостями кристалла 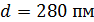 . Дифракционный максимум первого порядка наблюдается под углом
. Дифракционный максимум первого порядка наблюдается под углом 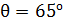 к атомной плоскости. Определите длину волны рентгеновского излучения
к атомной плоскости. Определите длину волны рентгеновского излучения 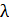 .
.
316. На диафрагму с узкой щелью падает нормально плоская монохроматическая световая волна с длиной волны 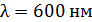 . Угол дифракции лучей, соответствующих второму дифракционному максимуму,
. Угол дифракции лучей, соответствующих второму дифракционному максимуму, 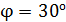 . Определите ширину щели
. Определите ширину щели 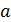 .
.
317. На дифракционную решетку, содержащую 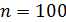 штрихов на одном миллиметре длины, падает нормально монохроматический свет. Зрительная труба спектрометра наведена на максимум второго порядка:
штрихов на одном миллиметре длины, падает нормально монохроматический свет. Зрительная труба спектрометра наведена на максимум второго порядка: 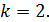 Чтобы навести трубу на другой максимум того же порядка
Чтобы навести трубу на другой максимум того же порядка 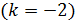 , ее нужно повернуть на угол
, ее нужно повернуть на угол 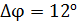 . Определите длину волны
. Определите длину волны 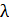 света, падающего на решетку.
света, падающего на решетку.
318. Дифракционная решетка длиной 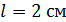 позволяет разрешить в спектре первого порядка две спектральные линии калия:
позволяет разрешить в спектре первого порядка две спектральные линии калия: 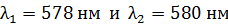 . Определите общее число щелей
. Определите общее число щелей 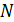 этой решетки и ее постоянную
этой решетки и ее постоянную 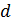 .
.
319. Постоянная дифракционной решетки 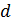 в 4 раза больше, чем длина световой волны монохроматического света
в 4 раза больше, чем длина световой волны монохроматического света 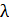 , падающего нормально на ее поверхность. Определите угол
, падающего нормально на ее поверхность. Определите угол 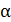 между первыми симметричными дифракционными максимумами.
между первыми симметричными дифракционными максимумами.
320. На дифракционную решетку, постоянная которой 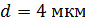 , падает нормально свет с длиной волны
, падает нормально свет с длиной волны 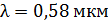 . Определите наибольший порядок максимума
. Определите наибольший порядок максимума 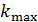 , который дает эта решетка, и угол дифракции
, который дает эта решетка, и угол дифракции 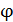 для этого максимума (
для этого максимума ( 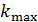 ).
).
Тепловое излучение
321. Вычислите истинную температуру 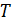 раскаленной вольфрамовой ленты, если радиационный пирометр показывает температуру
раскаленной вольфрамовой ленты, если радиационный пирометр показывает температуру 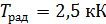 . Считайте, что поглощательная способность вольфрама
. Считайте, что поглощательная способность вольфрама 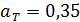 и не зависит от длины волны излучения.
и не зависит от длины волны излучения.
322. Температура абсолютно черного тела 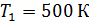 . Какова будет температура тела
. Какова будет температура тела 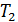 , если в результате нагревания поток излучения увеличится в
, если в результате нагревания поток излучения увеличится в 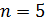 раз?
раз?
323. Температура абсолютно черного тела 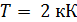 . Определите длину волны
. Определите длину волны 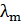 , на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости
, на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости 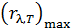 для этой длины волны.
для этой длины волны.
324. Определите температуру 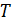 и энергетическую светимость
и энергетическую светимость 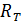 абсолютно черного тела, если максимум энергии излучения приходится на длину волны
абсолютно черного тела, если максимум энергии излучения приходится на длину волны 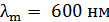 .
.
325. Из смотрового окна печи излучается поток энергии 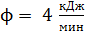 . Определите температуру
. Определите температуру 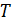 печи, если площадь окна
печи, если площадь окна 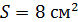 .
.
326. Поток излучения абсолютно черного тела 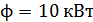 . Максимум энергии излучения приходится на длину волны
. Максимум энергии излучения приходится на длину волны 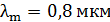 . Определите площадь
. Определите площадь 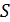 излучающей поверхности.
излучающей поверхности.
327. Как и во сколько раз изменится поток излучения 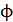 абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра:
абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра: 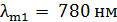 , на фиолетовую границу –
, на фиолетовую границу – 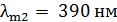 ?
?
328. Длина волны, на которую приходится максимум энергии излучения абсолютно черного тела 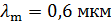 . Определите температуру тела
. Определите температуру тела 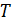 .
.
329. Муфельная печь, потребляющая мощность 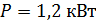 , имеет отверстие площадью
, имеет отверстие площадью 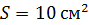 . Определите долю
. Определите долю 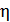 мощности, которая рассеивается стенками печи, если температура ее внутренней поверхности
мощности, которая рассеивается стенками печи, если температура ее внутренней поверхности 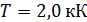 .
.
330. Средняя энергетическая светимость поверхности Земли 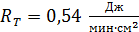 . Определите температуру
. Определите температуру 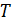 поверхности Земли, принимая, что она излучает как серое тело, имеющее поглощательную способность
поверхности Земли, принимая, что она излучает как серое тело, имеющее поглощательную способность 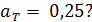
Фотоэффект
331. Красная граница фотоэффекта для цинка 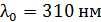 . Определите максимальную кинетическую энергию фотоэлектронов
. Определите максимальную кинетическую энергию фотоэлектронов 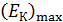 в джоулях и в электрон-вольтах, если на фотокатод падает свет с длиной волны
в джоулях и в электрон-вольтах, если на фотокатод падает свет с длиной волны 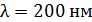 .
.
332. На поверхность калия падает свет с длиной волны 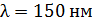 . Определите максимальную кинетическую энергию фотоэлектронов
. Определите максимальную кинетическую энергию фотоэлектронов 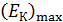 .
.
333. Фотон с энергией 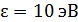 падает на серебряную пластинку и вызывает фотоэффект. Определите импульс
падает на серебряную пластинку и вызывает фотоэффект. Определите импульс 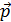 , полученный пластинкой, принимая, что скорости движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластинки.
, полученный пластинкой, принимая, что скорости движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластинки.
334. На фотоэлемент с катодом из лития падает свет с длиной волны 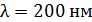 . Определите наименьшее значение задерживающей разности потенциалов
. Определите наименьшее значение задерживающей разности потенциалов 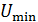 , которую нужно приложить к фотоэлементу, чтобы фототок стал равен нулю.
, которую нужно приложить к фотоэлементу, чтобы фототок стал равен нулю.
335. Какова должна быть длина волны 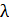 рентгеновского излучения, падающего на платиновую пластинку, чтобы максимальная скорость фотоэлектронов
рентгеновского излучения, падающего на платиновую пластинку, чтобы максимальная скорость фотоэлектронов 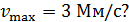
336. На металлический фотокатод направлен пучок ультрафиолетового излучения с длиной волны 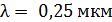 . Фототок прекращается, если приложить минимальную задерживающую разность потенциалов
. Фототок прекращается, если приложить минимальную задерживающую разность потенциалов 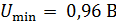 . Определите работу выхода
. Определите работу выхода  электронов из металла.
электронов из металла.
337. Излучение с длиной волны 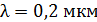 падает на поверхность металла. Красная граница фотоэффекта для него
падает на поверхность металла. Красная граница фотоэффекта для него 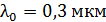 . Определите долю энергии фотона, которая расходуется на сообщение электрону кинетической энергии
. Определите долю энергии фотона, которая расходуется на сообщение электрону кинетической энергии 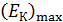 .
.
338. На металлический катод падает рентгеновское излучение с длиной волны 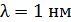 . Пренебрегая работой выхода, определите максимальную скорость фотоэлектронов
. Пренебрегая работой выхода, определите максимальную скорость фотоэлектронов 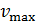 .
.
339. На металлическую пластинку направлен пучок света с частотой 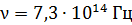 . Красная граница фотоэффекта для данного металла
. Красная граница фотоэффекта для данного металла 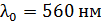 . Определите максимальную скорость фотоэлектронов
. Определите максимальную скорость фотоэлектронов 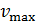 .
.
340. На цинковую пластинку направлен монохроматический пучок света. Фототок прекращается при задерживающей разности потенциалов 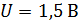 . Определите длину волны
. Определите длину волны 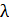 света, падающего на пластинку.
света, падающего на пластинку.
Темы лабораторных работ
Названия лабораторных работ, выполняемых студентами ЗИЭФ, и их номера в учебном пособии приведены в табл. 10.
Таблица 10
| Название работы | Номер работы |
| Исследование электростатического поля методом моделирования | 1 |
| Определение удельного заряда электрона методом магнетрона | 6 |
| Изучение зависимости магнитной проницаемости ферромагнетика от напряженности магнитного поля | 9 |
Подготовка к выполнению лабораторных работ
Методические указания к выполнению лабораторных работ: описание метода измерений, лабораторного стенда и схемы электрической цепи, порядок выполнения ЛР и обработки результатов измерений, – содержатся в следующем учебном пособии:
Электричество и магнетизм: учебное пособие к выполнению лабораторных работ по курсу физики / Л.Ф. Гладкова, А.Е. Гришкевич, С.И. Морозов и др.; под ред. А.Е. Гришкевича. – Челябинск: Изд-во ЮУрГУ, 2009. – 110 с.
Данное учебное пособие можно найти по следующему электронному адресу: http :// physics . susu . ac . ru / data / electr . pdf .
При подготовке к занятию в лаборатории настоятельно рекомендуем по каждой выполняемой ЛР заполнить некоторые разделы бланка отчета (до таблиц опытных данных): цель работы, описание установки и метода измерений (включая название величин, входящих в расчетные формулы).
Перед выполнением лабораторных работ необходимо изучить раздел 3.1 «Введение в лабораторный практикум по физике» (с. 40-48) – п. п. 3.1.1. Проведение лабораторного эксперимента; 3.1.2. Графическое представление и обработка результатов измерений; 3.3.1. Рекомендации к выполнению лабораторных работ и 3.3.2. Рекомендации к оформлению отчета по лабораторной работе.
МЕТОДОМ МОДЕЛИРОВАНИЯ
Bыполнил _______________
группа _____________
“____”____________20___г.
Проверил _______________
“____”____________20___г.
ЦЕЛЬ РАБОТЫ:
ЭЛЕКТРИЧЕСКАЯ СХЕМА И ОБОРУДОВАНИЕ
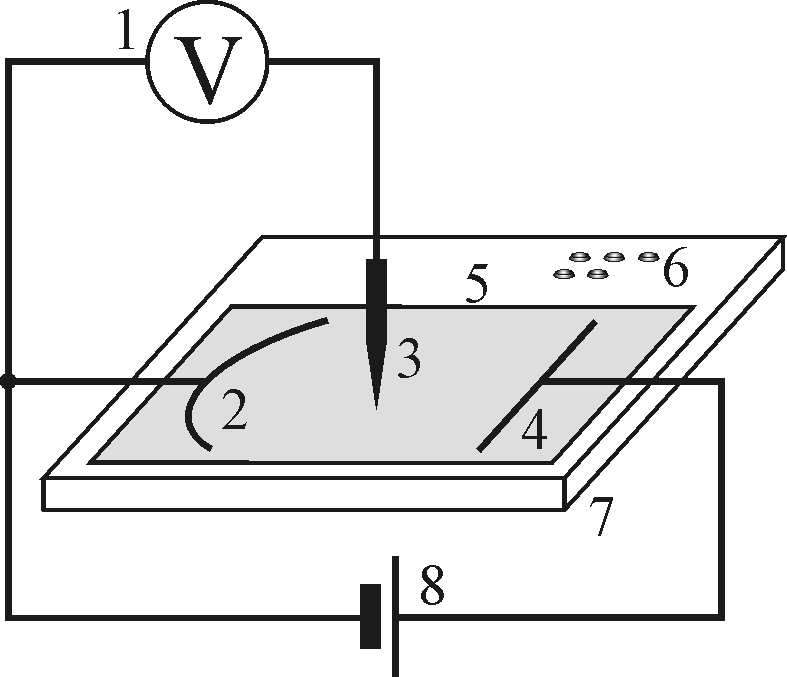
| 1 – 2 – 3 – 4 – 5 – 6 – 7 – 8 – |
Эквипотенциальная поверхность содержит точки с равным потенциалом. Силовая линия – линия, по касательной к которой направлен вектор напряженности 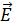 в каждой точке электростатического поля (ЭСП). Силовые линии проводят перпендикулярно эквипотенциальным поверхностям.
в каждой точке электростатического поля (ЭСП). Силовые линии проводят перпендикулярно эквипотенциальным поверхностям.
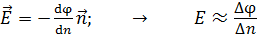 ,
,
где 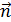 – единичный вектор нормали к эквипотенциальной поверхности.
– единичный вектор нормали к эквипотенциальной поверхности.
Изменение потенциала 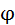 ЭСП с расстоянием
ЭСП с расстоянием 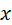 между электродами
между электродами
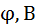
0 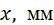
РАСЧЕТНАЯ ФОРМУЛА
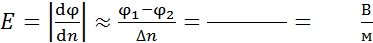 .
.
Здесь 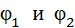 –
–
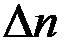 –
–
| Точки в электростатическом поле Точка | 
| 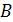
| 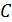
|
Напряженность ЭСП 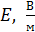
|
ВЫВОД
Картина силовых линий и эквипотенциальных поверхностей
исследуемого электростатического поля
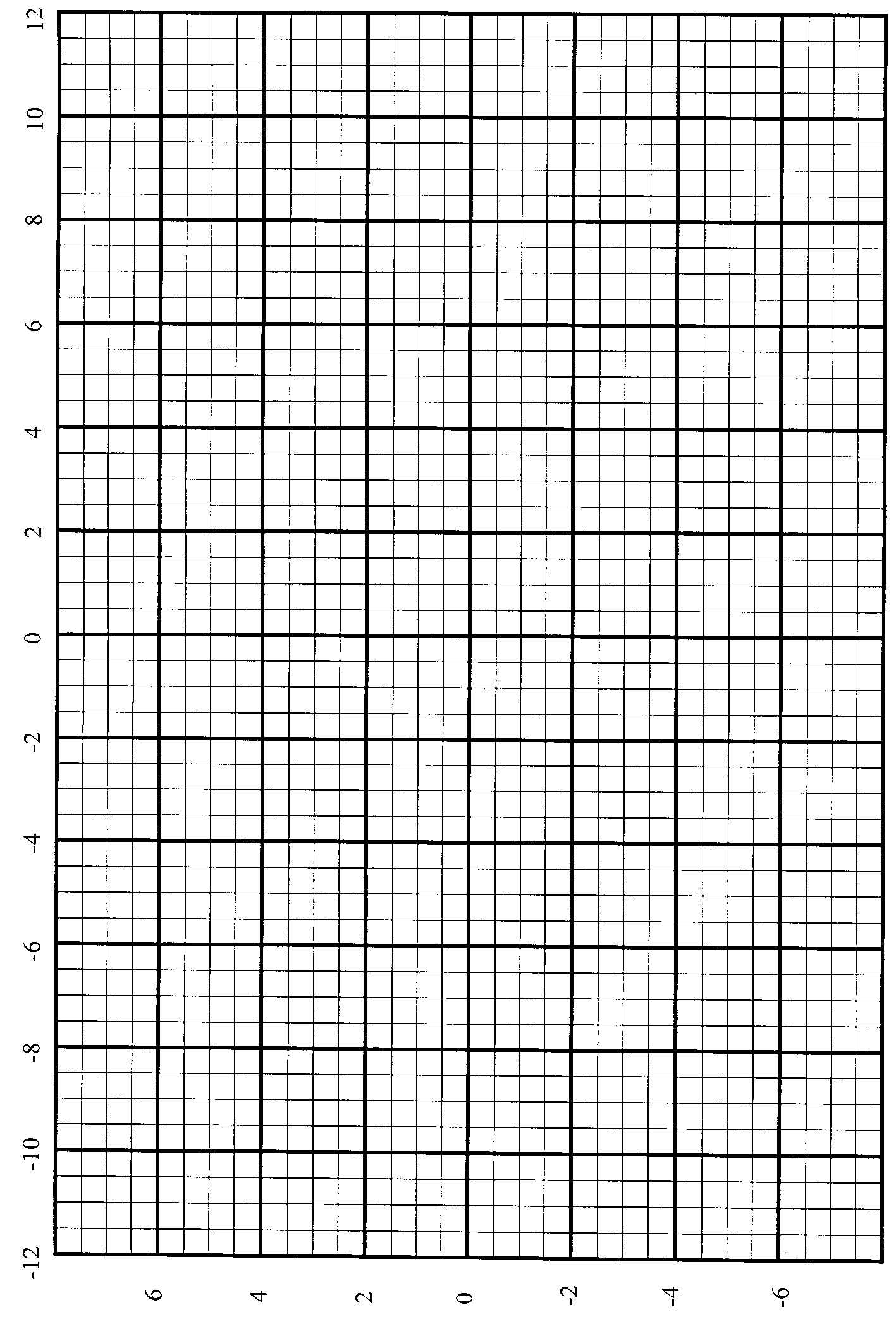
Южно-Уральский государственный университет
Кафедра физики наноразмерных систем
Лабораторная работа №6
МЕТОДОМ МАГНЕТРОНА
Выполнил_____________
группа _____________
“___”___________20___г.
Проверил ________
“___”___________20__ г.
ЦЕЛЬ РАБОТЫ:
ЭЛЕКТРИЧЕСКАЯ СХЕМА И ОБОРУДОВАНИЕ
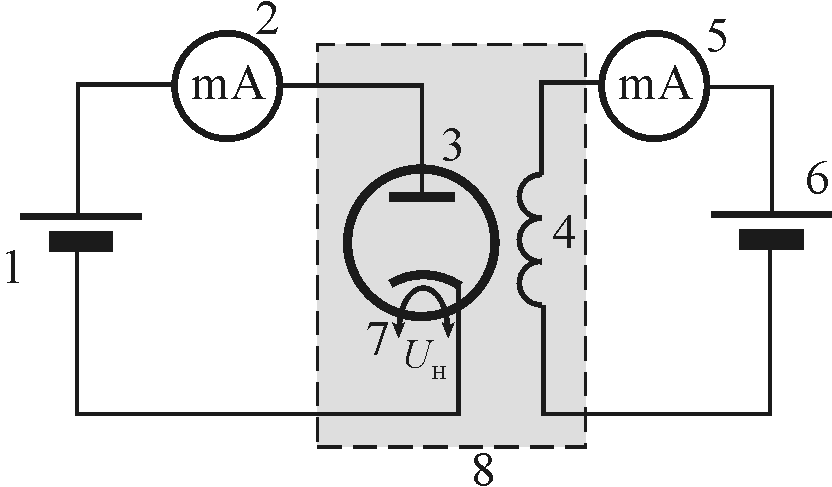
| 1 – 2 – 3 – 4 – 5 – 6 – 7 – 8 – |
МЕТОД ИЗМЕРЕНИЙ
|
| К |
| А |
помещенная в магнитное поле. Траектория
движения электронов в лампе (и анодный
ток) зависит от индукции магнитного поля.
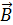 –
–
К –
А –
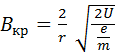 ,
,
Рис. 1 где 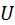 –
–
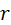 –
–
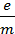 –
–
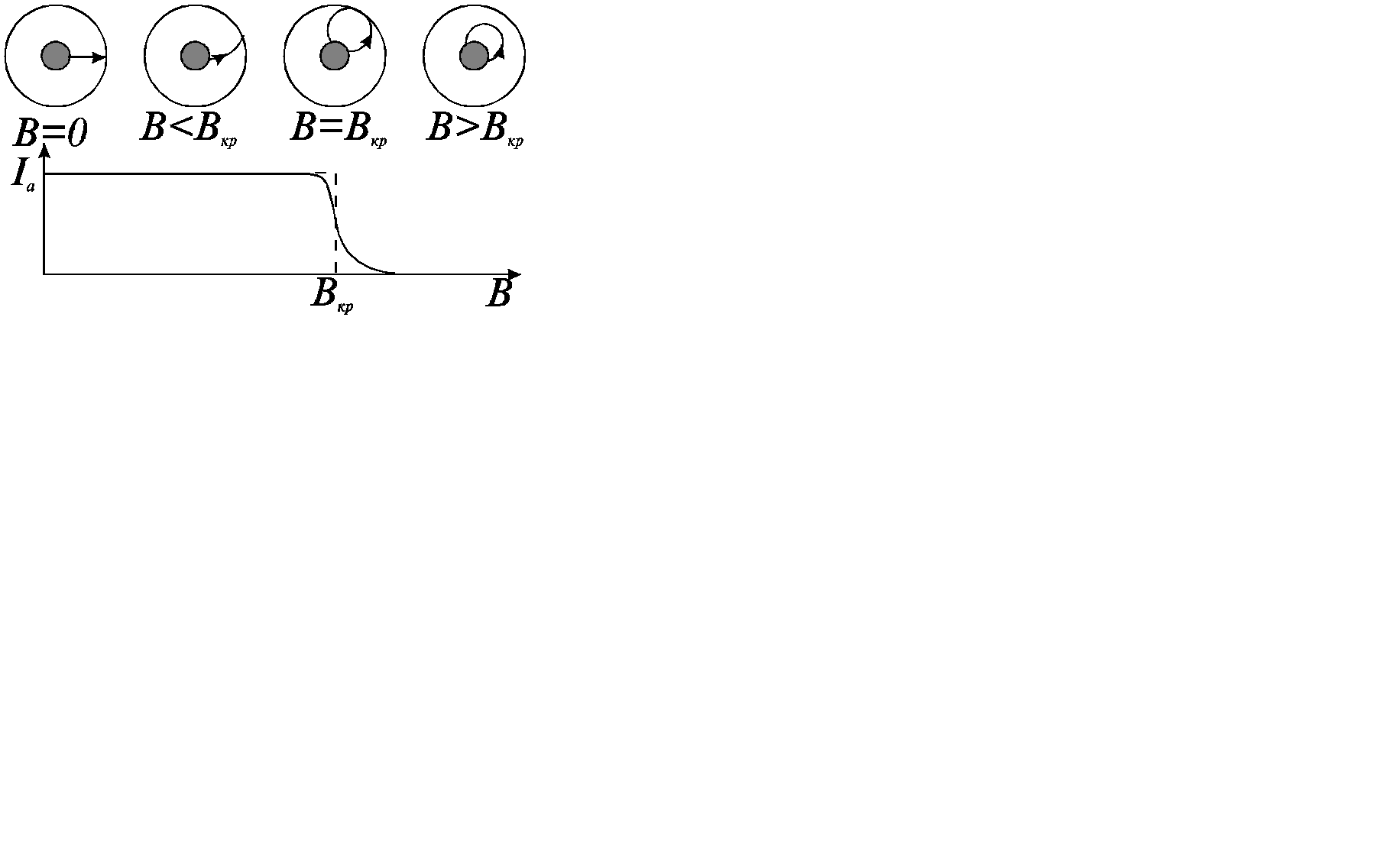 Рис. 2
Рис. 2
| 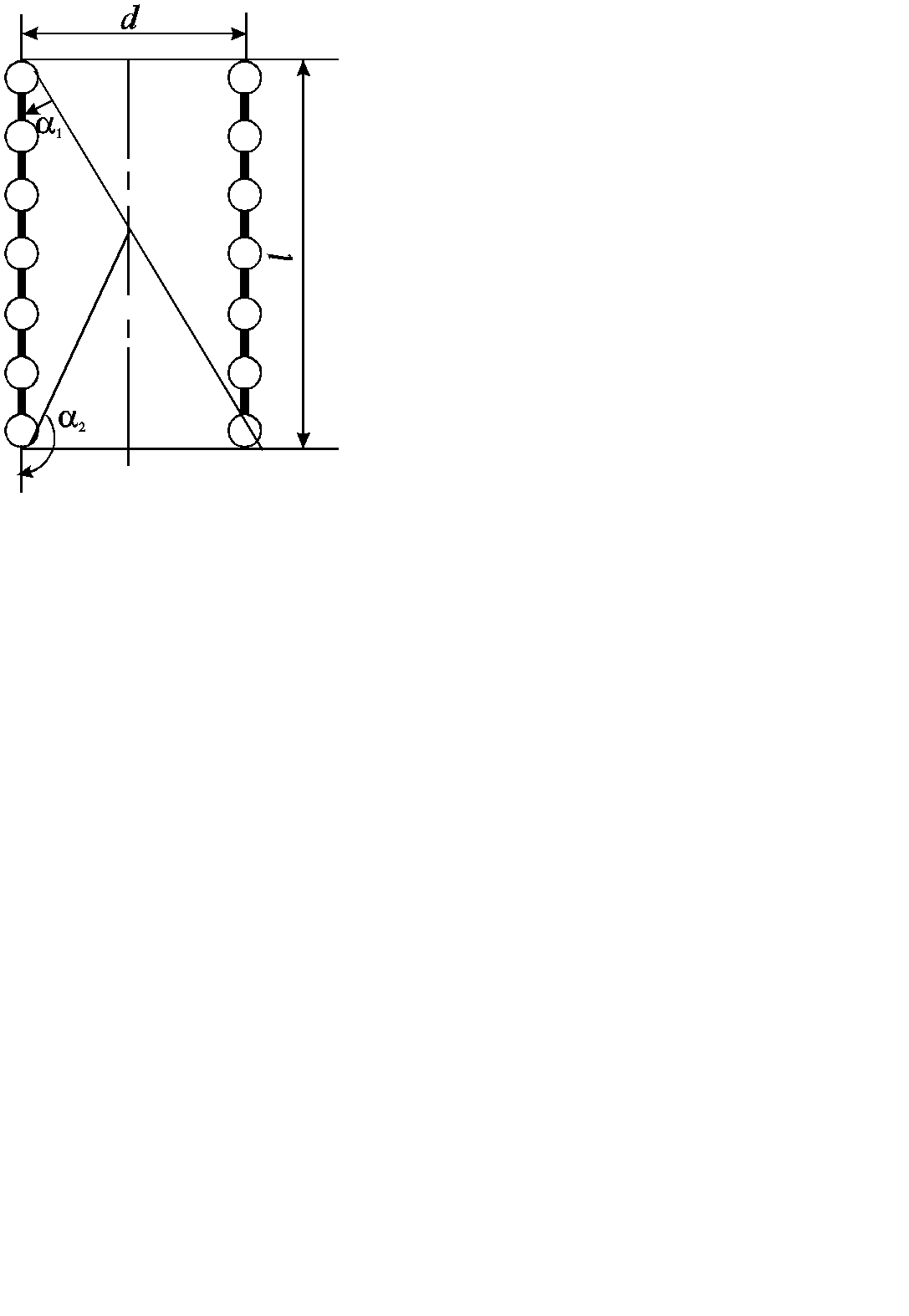 Рис. 3
Рис. 3
|
Критическое значение индукции магнитного поля соленоида
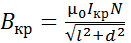 ,
,
где 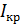 –
–
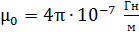 – магнитная постоянная.
– магнитная постоянная.
ОПЫТНЫЕ ДАННЫЕ
| ПАРАМЕТРЫ МАГНЕТРОНА | ТОК
СОЛЕНОИДА
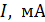
| АНОДНЫЙ
ТОК
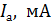
|
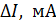
|
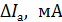
| 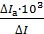 ,
условных ед. ,
условных ед.
|
| 90 | |||||
| 95 | |||||
| 100 | |||||
| 105 | |||||
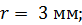
| 110 | ||||
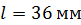 ; ;
| 115 | ||||
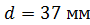 ; ;
| 120 | ||||
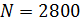 ; ;
| 125 | ||||
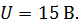
| 130 | ||||
| 135 | |||||
| 140 | |||||
| 145 | |||||
| 150 | |||||
| 155 | |||||
| 160 | |||||
| 165 | _________ |
Зависимость анодного тока магнетрона 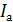 от тока
от тока 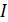 в соленоиде
в соленоиде
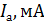
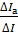
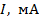
По графику определяем значение критического тока  .
.
РАСЧЕТ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА
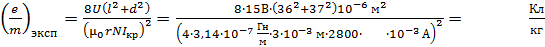 .
.
ОЦЕНКА ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
Сравниваем 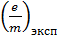 с табличным значением
с табличным значением 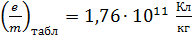 :
:
а) относительная погрешность измерения (показывает точность полученного результата):
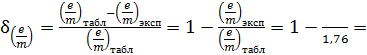 ; ( %).
; ( %).
б) абсолютная погрешность измеряемой величины (позволяет записать результат измерений в виде доверительного интервала):
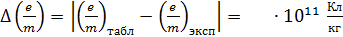 .
.
РЕЗУЛЬТАТ ИЗМЕРЕНИЙ
Удельный заряд электрона
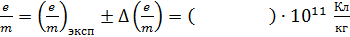 .
.
ВЫВОД
Южно-Уральский государственный университет
Кафедра физики наноразмерных систем
Лабораторная работа №9
ИЗУЧЕНИЕ ЗАВИСИМОСТИ
МАГНИТНОЙ ПРОНИЦАЕМОСТИ ФЕРРОМАГНЕТИКА
ПРИЛОЖЕНИЯ
Приложение 1
О приближенных вычислениях
Значения исходных величин в физических задачах, в том числе, и физических постоянных, как правило, получены в эксперименте и потому являются приближенными числами. При их записи оставлены только верные цифры числа (обычно это 2 или 3 значащие цифры).
Соответственно, и результат вычислений по расчетной формуле с подстановкой приближенных чисел имеет столько верных цифр, сколько их содержится в наименее точном числе (которое в формуле является слагаемым, сомножителем, или основанием степени).
Результат вычислений, полученный с помощью калькулятора, округляют, оставляя в нем только верные цифры.
Правила дифференцирования
Производная сложной функции 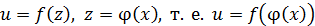 :
:
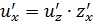 ; или
; или 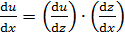 ;
;
Производная суммы (разности) функций u 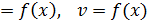 :
:
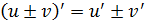 ; или
; или 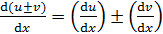 ;
;
Производная произведения функций u 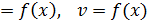 :
:
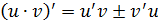 ; или
; или 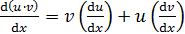 ;
; 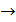
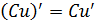 ; или
; или 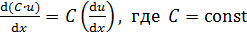 ;
;
Производная частного 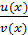 :
:
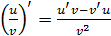 ; или
; или  ;
; 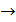
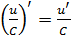 ; и
; и 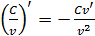 ;
; 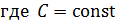 ;
;
Производные простейших функций:
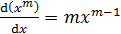 ;
; 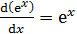 ;
; 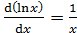 ;
; 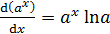 ;
;
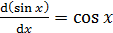 ;
; 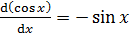 ;
; 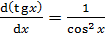 ;
; 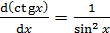 ;
;
Правила интегрирования
Интеграл суммы (разности) функций u 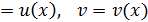 :
:
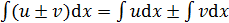 ;
;
Постоянный сомножитель 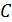 выносят за знак интеграла:
выносят за знак интеграла:
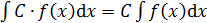 ;
;
Метод интегрирования по частям:
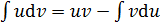 ;
;
Интегрирование простейших функций:
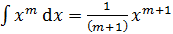 ; (при
; (при 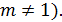
 ;
; 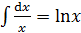 ;
;
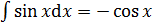 ;
; 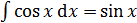 ;
; 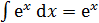 ;
;
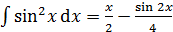 ;
; 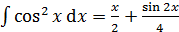 ;
;
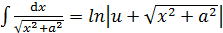 ;
; 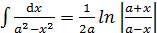 ;
;
ФИЗИКА
Практическое руководство для самостоятельной работы
студентов заочной формы обучения ПИ ЮУрГУ
Челябинск
Издательский центр ЮУрГУ
2018
УДК 530.1(075.8)
М641
Одобрено
учебно-методической комиссией Института
естественных и точных наук
Рецензенты:
Л.А. Песин, В.К. Усачев
Миронова Т.О.
М.641 Физика: практическое руководство для самостоятельной работы студентов заочной формы обучения ПИ ЮУрГУ / Т.О. Миронова, Ю.Б. Пейсахов, Т.П. Привалова. – Челябинск: Издательский центр ЮУрГУ, 2018. – 124 с.
Основное назначение учебного пособия – оказать помощь по изучению курса общей физики студентам заочной формы обучения. Учебное пособие является руководством в организации работы студентов в течение двух семестров. В пособии даны программные вопросы по курсу физики, варианты и задачи контрольных работ, изложены требования к выполнению контрольных работ и к оформлению решений задач, а также содержатся методические материалы для выполнения лабораторных работ и рекомендации по оформлению отчетов.
Учебное издание предназначено для студентов, обучающихся по укрупненным группам специальностей и направлений подготовки в области образования «инженерное дело, технологии и технические науки».
УДК 530.1(075.8)
© Издательский центр ЮУрГУ, 2018
ОГЛАВЛЕНИЕ
Введение ….…………………………………………………………… . . . . 5
Часть I
МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА.
Дата: 2019-11-01, просмотров: 408.
 ;
; 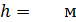 ;
;  ;
;  ;
;