«Решение обыкновенных
Дифференциальных уравнений»
Цель работы: Изучение средств Scilab для решения обыкновенных дифференциальных уравнений (ОДУ)1-го и 2-го порядка, а также систем ОДУ, получение решения ОДУ в виде таблицы и графика.
2.5.1. Вопросы, подлежащие изучению
1) Постановка задачи решения ОДУ [7].
2) Функция ode, предназначенная для решения ОДУ.
3) Вывод результатов решения ОДУ в виде таблицы.
4) Получение графического решения ОДУ.
5) Решение ОДУ 2-го порядка с использованием функции ode.
2.5.2. Общее задание
1) Изучить материал учебника [1] (п. 2.5).
2) Выбрать индивидуальный вариант задания из табл. 2.5-1.
3) Создать сценарии для выполнения практического задания.
4) Найти решение ОДУ на отрезке [ x 0 ; b ] с шагом h с использованием функции ode.
5) Создать матрицу решений, записав в первый столбец аргумент, а во второй - решение, полученное с использованием функций ode.
6) Вывести полученную таблицу по столбцам.
7) Построить график полученного решения ОДУ.
8) Выбрать индивидуальный вариант задания из табл. 2.5-2.
9) Создать сценарий для решения системы ОДУ или решения ОДУ 2-го порядка согласно вашему варианту.
10) Найти решение системы ОДУ, вывести матрицу решения и построить график решения системы ОДУ.
11) Спроектировать и реализовать приложение: «Решение обыкновенных дифференциальных уравнений» для ввода данных и отображения результатов (по требованию преподавателя).
12) Предоставить результаты работы преподавателю и ответить на поставленные вопросы.
13) Оформить отчет по выполненной работе.
Варианты индивидуальных заданий
Таблица 2.5-1
| № | ОДУ | Начальные условия | b | h |
| 1 | 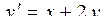
| 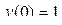
| 6 | 0,25 |
| 2 | 
| 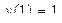
| 7 | 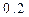
|
| 3 | 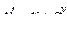
| 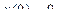
| 1.2 | 0.1 |
| 4 | 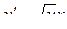
| 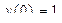
| 4 | 0,1 |
| 5 | 
| 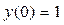
| 6 | 0,25 |
| 6 | 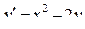
| 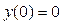
| 4 | 0.1 |
| 7 | 
| 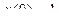
| 1.4 | 0,2 |
| 8 | 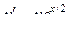
| 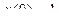
| 1.5 | 0,2 |
| 9 | 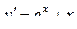
| 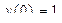
| 5 | 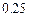
|
| 10 | 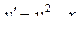
| 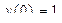
| 6 | 0,25 |
| 11 | 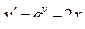
| 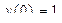
| 4 | 0,1 |
| 12 | 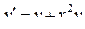
| 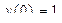
| 6 | 0,25 |
| 13 | 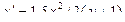
| 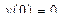
| 2,5 | 0.25 |
| 14 | 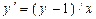
| 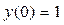
| 2 | 0,1 |
| 15 | 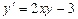
| 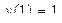
| 4 | 0,25 |
| 16 | 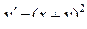
| 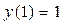
| 3 | 0,25 |
| 17 | 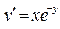
| 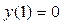
| 5 | 0,25 |
| 18 | 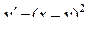
| 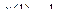
| 5 | 0,25 |
| 19 | 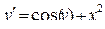
| 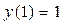
| 6 | 0,5 |
| 20 | 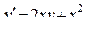
| 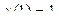
| 4 | 0,25 |
| 21 | 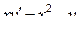
| 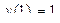
| 2 | 0.1 |
| 22 | 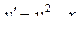
| 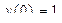
| 8 | 0,25 |
| 23 | 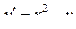
| 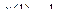
| 2,5 | 0,25 |
| 24 | 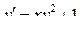
| 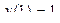
| 6.5 | 0.25 |
| 25 | 
| 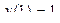
| 5.5 | 0,25 |
| 26 | 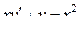
| 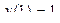
| 4 | 0,125 |
| 27 | 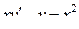
| 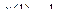
| 5 | 0,5 |
| 28 | 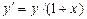
| 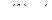
| 4,4 | 0,2 |
| 29 | 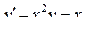
| 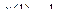
| 5 | 0,2 |
| 30 | 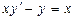
| 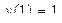
| 7 | 0.5 |
Таблица 2.5-2
| № | Система ОДУ или ОДУ 2-го порядка | Начальные условия | b | h |
| 1 | 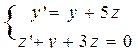
| y(0)=2, z(0)=1 | 2 | 0,2 |
| 2 | 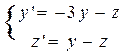
| y(0)=1, z(0)=5 | 1 | 0,1 |
| 3 | 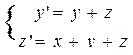
| y(0)=1, z(0)=1/4 | 1 | 0 , 1 |
| 4 | 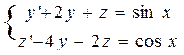
| y(π)=0, z(π)=3 | 2π | π/6 |
| 5 | 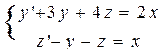
| y(0)=0, z(0)=0 | 1 | 0,1 |
| 6 | 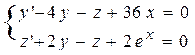
| y(0)=0, z(0)=0 | 1 | 0,1 |
| 7 | 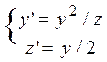
| y(0)=2, z(0)=1 | 2 | 0,2 |
| 8 | 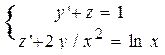
| y(1)=1, z(1)=0 | 2 | 0,1 |
| 9 | 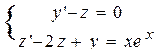
| y(0)=2, z(0)=-1 | 2 | 0,2 |
| 10 | 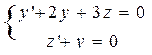
| y(0)=1, z(0)=0 | 2 | 0,2 |
| 11 | 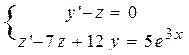
| y(0)=1, z(0)=0 | 1 | 0,1 |
| 12 | 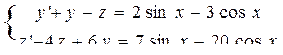
| y(0)=1, z(0)=7 | 2 | 0,2 |
| 1 3 | 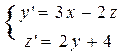
| y(0)=2, z(0)=3 | π | π /6 |
| 14 | 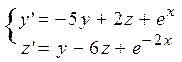
| y(0)=0, z(0)=-1/20 | 2 | 0 ,2 |
| 15 | 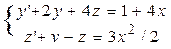
| y(0)=0, z(0)=1 | 2 | 0 ,2 |
| 16 | y’’– 2y’+ y=ex(x2+1) | y(0)=1, y’(0)=2 | 2 | 0 ,2 |
| 17 | y’’+ 3y’+2y=2cos(3x)+4sin(3x) | y(0)=1, y’(0)=2 | 4 | 0 ,4 |
| 18 | y’’+ y’=x sin(x) | y(0)=1, y’(0)=4 | 2 | 0 ,2 |
| 19 | y’’– 2y’+y = 2ex | y(0)=2, y’(0)=5 | 1 | 0 ,1 |
| 20 | y’’– 2y’– 8y = e2x+5 | y(0)=3, y’(0)=1 | 1 | 0 ,1 |
| 21 | y’’+ y’ = 5x+2ex | y(0)=1, y’(0)=3 | 2 | 0 ,2 |
| 22 | y’’– y’ = 2x – 1 – 3e-x | y(0)=1, y’(0)=4 | 2 | 0 ,2 |
| 23 | y’’ – y’ = 2x sin(x) | y(0)=2, y’(0)=2 | 2 | 0 ,2 |
| 24 | y’’+ y’ = cos(3x) | y(π/2)=4, y’(π/2)=1 | 2π | π /4 |
| 25 | y’’+2y’+y = e-x | y(0)=1, y’(0)=2 | π | π /6 |
| 26 | y’’ – 4 y’+4y = x2 | y(0)=1, y’(0)=2 | 1 | 0 ,1 |
| 27 | y’’– 2y =ex | y(0)=1, y’(0)=4 | 2 | 0 ,2 |
| 28 | y’’+ 4y =sin(x) | y(0)=1, y’(0)=1 | π | π /6 |
| 29 | y’’– 2y’+5y=ex +cos(2x) | y(0)=1, y’(0)=1 | π | π /6 |
| 30 | y’’ – 8y’ +7y=14 | y(0)=1, y’(0)=2 | 1 | 0 ,1 |
Содержание отчета
1) Титульный лист
2) Название и цель практического занятия
3) Общее задание
4) Графический интерфейс пользователя
5) Сценарии, вначале которых должна быть введена информация в виде комментариев:
· имя и назначение сценария;
· вариант индивидуального задания и номер задания.
6) Протокол сессии Командного окна, вначале которой должна быть введена информация в виде комментариев:
· название практического занятия;
· вариант индивидуального задания и номер задания;
· ФИО студента, номер группы;
· краткое перечисление действий, выполняемых во время сессии.
2.5.5. Контрольные вопросы по теме
1) Какие начальные условия должны быть заданы в соответствии с задачей Коши при решении ОДУ средствами системы Scilab?
2) В чем отличие аналитического решения ОДУ от численного?
3) Какие численные методы реализованы в функции ode?
4) Какие параметры являются в функции ode обязательными?
5) В какой форме должно быть записано ОДУ при использовании ode?
6) Какими средствами решается система ОДУ?
7) Что такое порядок ОДУ?
8) Что представляет собой решение ОДУ 1-го и 2-го порядка при использовании функции ode?
Дата: 2019-11-01, просмотров: 448.