«Интегрирование и дифференцирование
в среде Scilab»

Цель работы: Изучение возможностей вычисления значений определенных интегралов, а также значений производной в точке с использованием функций Scilab.  

Вопросы, подлежащие изучению

1) Постановка задачи численного интегрирования [7].

2) Вычисление значения определенного интеграла с использованием функций inttrap и integrate.

3) Вычисление значения производной в точке с использованием функций Scilab numderivative.

4) Методы численного интегрирования: метод трапеций и метод Симпсона.

2.3.2. Общее задание

1) Изучить материал учебника [1](п. 2.3).

2) Выбрать из табл. 2.3-1 вариант индивидуального задания.

3) Создать сценарии для выполнения практического задания.

4) Описать подынтегральную функциюf ( x ).

5) Вычислить определенный интеграл с использованием функции inttrap ( x , y ), реализующей формулу трапеций, получив предварительно таблицу значений подынтегральной функции с шагом h, и задав значения аргумента и функции в виде векторов.

6) Вычислить значение определенного интеграла с различной точностью, используя функцию integrate (' f ', a , b ), реализующей формулу Симпсона, где f – имя подынтегральной функции, взятое в одинарные кавычки.

7) Вычислить производную от функции y ( x )в нескольких точках, задавая их значения как вектор аргументов. Затем вычислить производную в этих же точках по отдельности. Сравнить результаты.

8) Спроектировать и реализовать приложение: «Интегрирование и дифференцирование в среде Scilab» для ввода данных и отображения результатов (по требованию преподавателя).

9) Предоставить результаты работы преподавателю и ответить на поставленные вопросы.

10) Оформить отчет по выполненной работе.

Варианты индивидуальных заданий

Таблица 2.3-1

№	Интеграл	y(x)	№	Интеграл	y(x)
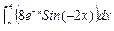
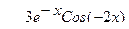
1			16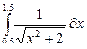
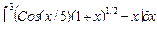
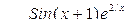
2			17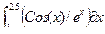
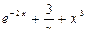
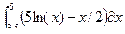
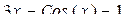
3			18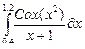
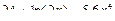
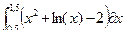
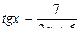
4			19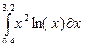
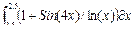
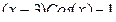
5			20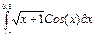
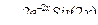
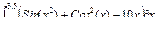
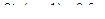
6			21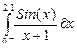
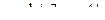
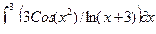
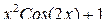
7			22
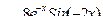
8		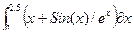	23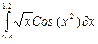
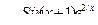
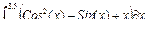
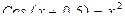
9			24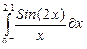
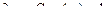
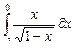
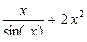
10			25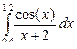
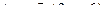
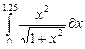
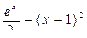
11			26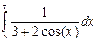
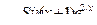
12		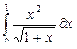	27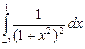
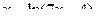
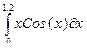
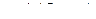
13			28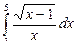
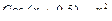
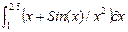
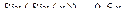
14			29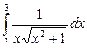
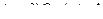
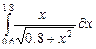
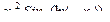
15			30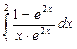

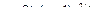
Содержание отчета

1) Титульный лист

2) Название и цель практического занятия

3) Общее задание

4) Графический интерфейс пользователя

5) Сценарии, вначале которых должна быть также введена информация в виде комментариев:

· имя и назначение сценария;

· вариант индивидуального задания и номер задания.

6) Протокол сессии Командного окна, вначале которой должна быть введена информация в виде комментариев:

· название практического занятия;

· вариант индивидуального задания и номер задания;

· ФИО студента, номер группы;

· краткое перечисление действий, выполняемых во время сессии.

2.3.5. Контрольные вопросы по теме

1) Что такое определенный интеграл?

2) Каково назначение функции inttrap?

3) Что возвращает функция inttrap , если y ( x ) – матрица?

4) Можно ли использовать функцию inttrap , если узлы по оси х – не равноотстоящие?

5) Каким образом вычислить интеграл, если подынтегральная функция задана таблицей с не равноотстоящими узлами?

6) Какая функция Scilab позволяет вычислить определенный интеграл с заданной точностью?

7) Какой численный метод заложен в функции integrate?

8) Какие существуют способы задания подынтегральной функции при вычислении определенного интеграла с использованием функции integrate?

9) Как задать допустимую погрешность вычисления определенного интеграла?

10) С какой точностью производится вычисление определенного интеграла, если погрешность не задана?

11) Какой встроенной функцией системы Scilab вычисляется производная в заданной точке?

12) Какое назначение и формат имеет функции numderivative?

13)