«Решение нелинейных уравнений»
Цель работы: Изучение средств решения нелинейных уравнений в Scilab, реализации этапов отделения и уточнения корней нелинейных уравнений.
Вопросы, подлежащие изучению
1) Постановка задачи решения нелинейных уравнений [7].
2) Этапы решения нелинейных уравнений: отделение и уточнение корня.
3) Графическое и аналитическое отделение корней нелинейных уравнений.
4) Построение графиков функций нелинейных уравнений средствами Scilab.
5) Получение таблиц значений функций и производных в заданных границах изменения аргумента.
6) Решение нелинейных уравнений с использованием встроенных функций пакета Scilab: fsolve,polyи roots.
2.4.2. Общее задание
1) Изучить материал учебника [1] (п. 2.4).
2) Выбрать индивидуальный вариант задания из табл. 2.4-1.
3) Создать сценарий для выполнения практического задания.
4) Отделить корень нелинейного уравнения f ( x )=0 с использованием средств пакета Scilab , для чего необходимо:
· построить графики функции f ( x )и ее первой производной ;
· выбрать отрезок, на котором существует один корень;
· получить таблицы значений аргумента, функции f ( x )и ее первой производной на выбранном отрезке пересечения графика с осью ОХ, причем для вычисления производной воспользуйтесь функцией numderivative;
· проверить условие существования единственного корня на выбранном отрезке.
5) Решить 1-е нелинейное уравнение с использованием fsolve, получив значение корня и значение функции в точке корня.
6) Задать для 2-го уравнения вектор коэффициентов.
7) Сформировать с использованием функции poly полином с коэффициентами, хранящимися в векторе.
8) Вычислить корни полученного полинома, используя функцию roots.
9) Спроектировать и реализовать приложение: «Решение нелинейных уравнений» для ввода данных и отображения результатов (по требованию преподавателя).
10) Предоставить результаты работы преподавателю и ответить на поставленные вопросы.
11) Оформить отчет по выполненной работе.
Варианты индивидуальных заданий
Таблица 2.4 -1
| № | Уравнение | № | Уравнение |
| 1 | 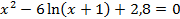

| 16 | 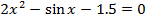

|
| 2 | 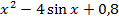 =0 =0
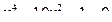
| 17 | 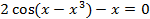
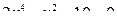
|
| 3 | 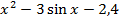

| 18 | 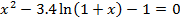
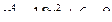
|
| 4 | 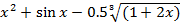 =0 =0

| 19 | 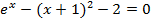

|
| 5 | 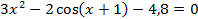

| 20 | 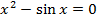

|
| 6 | 

| 21 | 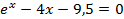

|
| 7 | 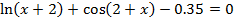

| 22 | 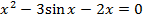

|
| 8 | 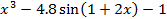 =0 =0

| 23 | 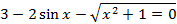
|
| 9 | 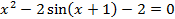

| 24 | 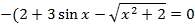

|
| 10 | 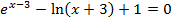

| 25 | 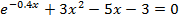
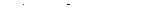
|
| 11 | 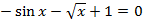
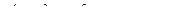
| 26 | 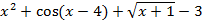 =0 =0

|
| 12 | 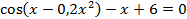

| 27 | 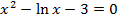

|
| 13 | 
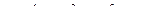
| 28 | 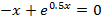

|
| 14 | 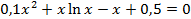

| 29 | 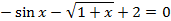
|
Содержание отчета
1) Титульный лист
2) Название и цель практического занятия
3) Общее задание
4) Графический интерфейс пользователя
5) Сценарии, вначале которых должна быть введена информация в виде комментариев:
· имя и назначение сценария;
· вариант индивидуального задания и номер задания.
6) Протокол сессии Командного окна, вначале которой должна быть введена информация в виде комментариев:
· название практического занятия;
· вариант индивидуального задания и номер задания;
· ФИО студента, номер группы;
· краткое перечисление действий, выполняемых во время сессии.
2.4.5. Контрольные вопросы по теме
1) Что называется нелинейным уравнением?
2) Из каких этапов состоит решение нелинейного уравнения численным методом?
3) В чем состоит графический метод отделения корней нелинейного уравнения и как он реализуется средствами Scilab?
4) В чем состоит аналитический метод отделения корней нелинейного уравнения и как он реализуется средствами Scilab?
5) Как задается функция нелинейного уравнения при его решении с использованием функции fsolve?
6) Какая функция Scilab позволяет решить нелинейное уравнение с заданной точностью?
7) В чем назначение и каков формат функции fsolve?
8) Для каких нелинейных уравнений в ходе их решения используется функция poly?
9) Какие нелинейные уравнения решаются с использованием функции roots?
10) Какая функция Scilab позволяет найти как действительные, так и мнимые корни нелинейного уравнения?
11) Какие выходные параметры могут иметь функции fsolve и roots?
12) Как проверить правильность полученных корней нелинейного уравнения?
Дата: 2019-11-01, просмотров: 493.