Пусть функция 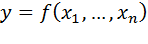 определена в окрестности точки

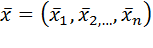. Говорят, что  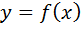имеет в точке x максимум (минимум), если существует d -окрестность точки x, такая, что для всех точек этой окрестности выполняется неравенство f ( 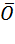) ³ f ( 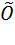) (f ( 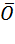) £ f ( )).

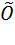Если для всех точек d -окрестности точки x имеет место строгое неравенство, то говорят, что функция имеет строгий максимум (минимум). Точки максимума и минимума функции нескольких переменных, как и для функции одной переменной, называются точками экстремума.

Теорема: (необходимое условие экстремума).

Предположим, что в точке x функция f имеет экстремум. Тогда, если функция f дифференцируема в этой точке, то

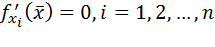
Таким образом, равенство нулю частных производных является необходимым условием существования экстремума. Как и в случае одной переменной, точки, в которых все частные производные равны нулю, называются стационарными. В стационарных точках не обязательно будет экстремум, т.е. равенство нулю частных производных – условие необходимое, но не достаточное.

Теорема: (достаточное условие локального экстремума функции двух переменных).

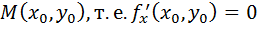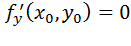Пусть функция z = f (x, y) имеет непрерывные частные производные второго порядка в некоторой окрестности стационарной точки  и . Обозначим:

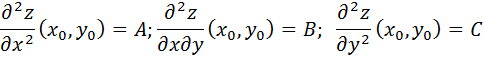
Тогда, если

,

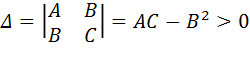то в точке функция z = f (x,y) имеет экстремум, причем, если A < 0 – максимум, а если A > 0 – минимум. В случае 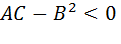функция z=f(x,y) экстремума не имеет. Если  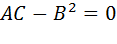= , то это правило не дает ответа на вопрос о существовании экстремума. Нужны дополнительные условия.

Следует отметить, что значение определителя D зависит от координат точек, в которых вычисляются частные производные, поэтому вычисляется в каждой стационарной точке.

Достаточные условия строгого экстремума для функции n переменных могут быть сформулированы в виде следующей теоремы.

Пусть функция 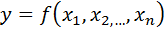дважды непрерывно дифференцируема в окрестности точки 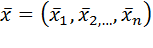. Тогда точка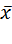  

1) является точкой строгого минимума функции, если

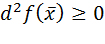
для любых достаточно малых приращений D 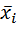 , причем равенство имеет место только при условии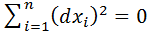

2) является точкой строгого максимума функции, если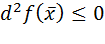

для любых достаточно малых приращений D 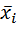, причем равенство имеет место только при условии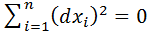

3) не является точкой экстремума, если принимает 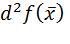как положительные, так и отрицательные значения.

Эти условия не являются необходимыми.

Для исследования стационарных точек функции трех и большего числа переменных рассмотрим матрицу, составленную из частных производных второго порядка функции 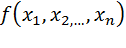 , которая имеет вид:

где все производные вычислены в точке 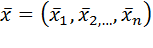, подозрительной на экстремум. Такая матрица носит название матрицы Гессе. Главными минорами матрицы называются определители матриц, образованные из элементов, стоящих на пересечении первых k строк и k столбцов матрицы,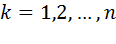

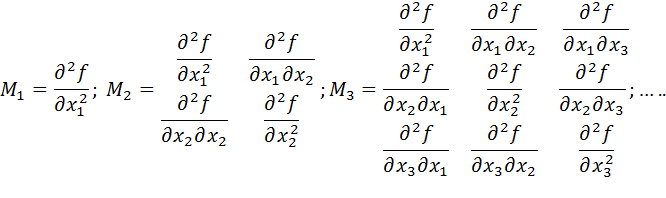
Теорема:

Пусть функция 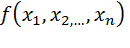имеет в точке 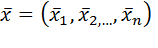непрерывные частные производные второго порядка, причем

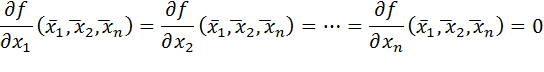
Тогда:

1. Если все главные миноры матрицы Гессе положительны, то функция 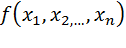 имеет в точке 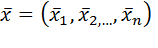локальный минимум.

2. Если все главные миноры порядка k положительны при четных k и отрицательны при нечетных k , то функция 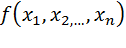имеет в точке  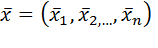локальный максимум.

3. Если среди главных миноров матрицы Гессе есть хотя бы один отрицательный, то функция 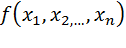 не имеет в точке 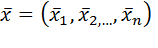локального минимума.

4. Если хотя бы один главный минор четного порядка отрицателен или хотя бы один главный минор нечетного порядка положителен, то функция 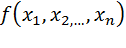не имеет в точке 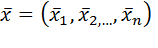локального максимума.

Заметим, что теорема о достаточном условии экстремума функции двух переменных является частным случаем последней теоремы.

Условный экстремум.

Пусть в области n D Ì R определена функция 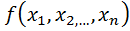 и система функций 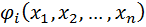,  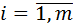и пусть множество  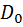является областью допустимых значений системы уравнений

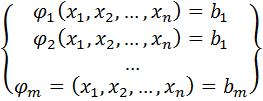
Задача нахождения условного экстремума ставится следующим образом. Найти локальный экстремум функции 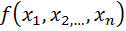 на множестве 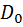, или, другими словами, найти:

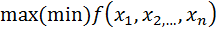
при ограничениях, заданных уравнениями связи (системы).

Для нахождения условного экстремума вводится функция Лагранжа:

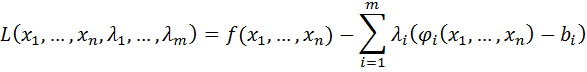
где 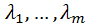 – множители Лагранжа. Если ввести вектора 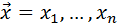, , 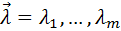 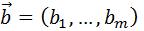и вектор-функцию  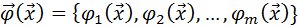, то функцию Лагранжа можно записать следующим образом:

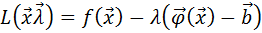
Теорема:

Предположим, что в точке 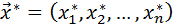функция 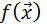имеет условный локальный экстремум, ранг матрицы

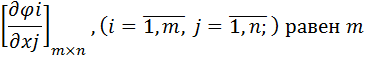
Тогда точка ( 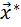, 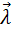) является стационарной точкой функции Лагранжа, и необходимые условия экстремума запишутся в виде:

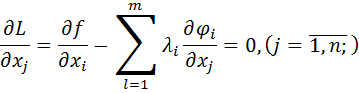
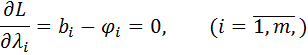
Существуют также и достаточные условия, при выполнении которых решение системы данных уравнений определяет точку экстремума функции 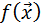. Этот вопрос решается на основании исследования знака второго дифференциала функции Лагранжа. Однако достаточные условия представляют главным образом теоретическое значение.