Дифференцирование сложной функции.

Пусть z=f(u,v) – дифференцируемая функция двух переменных u и v ; причем u и v, в свою очередь, дифференцируемые функции от х, т.е. u= j(x), v=f(x). Тогда можно доказать существование производной сложной функции и вычислить ее.

Найдем 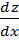. С этой целью придадим аргументу x приращение Dx. Тогда u получит приращение Du, V–DV, а z–Dz. Для полного приращения справедлива формула:

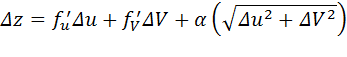
где x зависит от Dx и a ® 0 при Dx ® 0.

Разделим обе части равенства на Dx, и перейдем к пределу, устремив Dx к нулю:

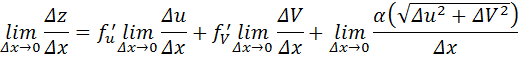
При Dx ® 0 будем иметь, что Du ® 0 и DV ® 0 (по непрерывности u и v, которая следует из их дифференцируемости). При этом a – бесконечно малая функция более высокого порядка, чем Dx. Последнее означает, что

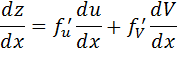
Эта формула остается справедливой и для случая, когда функция f является функцией n переменных:

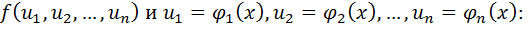
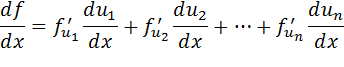
Пример: 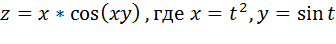. Найти: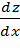

По формуле:
 

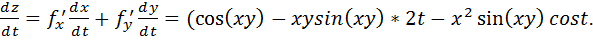
Рассмотрим теперь случай, когда функция z=f(u,v), а u и V являются функциями двух переменных x и у: u=j(x,y), v=f(x,y), т.е. z=f(j(x,y),f(x,y)).

Будем считать, что функции f, j и f имеют непрерывные частные производные, тогда справедливы формулы

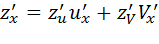
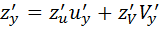
Если задана функция m переменных вида: 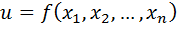, где

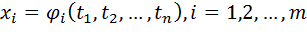 дифференцируемая в точке M с координатами  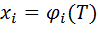(здесь T – точка с координатами а функции 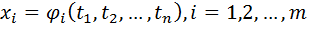 дифференцируемы в T  то сложная функция

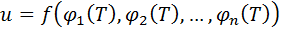дифференцируема в точке T. При этом частные производные сложной функции определяются по формуле

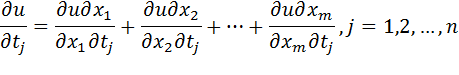
Здесь частные производные функции берутся в точке M, а частные производные функций 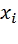 по аргументам  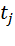берутся в точке T.

Пример: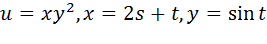

Применяем формулы
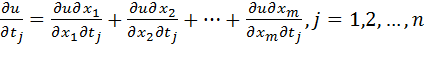, а именно

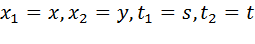
Получаем:

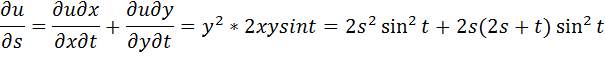
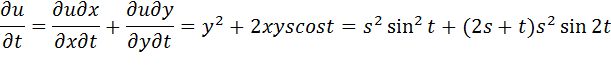
Дифференцирование неявной функции.

Неявной функцией z двух независимых переменных x и у называется функция, определяемая уравнением, связывающим переменные x, y и z и неразрешенном относительно z: f (x, y, z) = 0.

Теорема:

Если f(x, y, z) определена и непрерывна в какой-нибудь окрестности точки 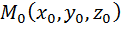, причем 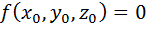, а ее частные производные  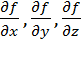существуют и непрерывны в указанной окрестности, и  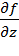не обращается в нуль в точке 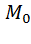, то уравнение f(x,y,z)=0 в некоторой окрестности 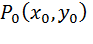определяет z как непрерывную функцию от x и y , z =j(x,y), обращающуюся в 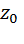в точке 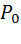. Функция z =j(x,y) имеет непрерывные частные производные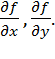  

Производная по направлению.

Пусть y = f (x) функция n переменных, дифференцируемая в точке

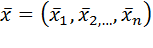 . Зададим в точке  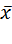направление с помощью вектора

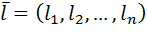. Напомним, что длина вектора  вычисляется по формуле

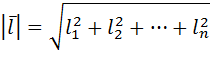
Производной функции n переменных f (x) в направлении вектора 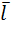называется величина

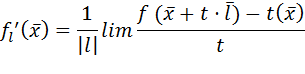
Производная по направлению обозначается также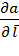

Производная по направлению координатных осей совпадает с соответствующими частными производными. Производная по направлению может быть вычислена по формуле

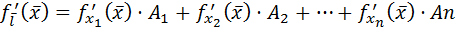
где величины , называемые направляющими косинусами вектора  , вычисляются по формуле: 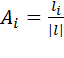. Для функции трех переменных формула  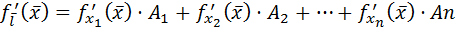имеет вид:

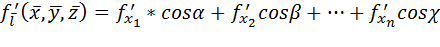
Здесь a, b, c – углы, которые вектор  составляет с осями координат.

Производная по направлению определяет скорость изменения функции y=f(x) в точке x в направлении вектора . Формула

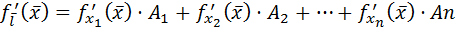 представляет собой скалярное произведение двух векторов: вектора 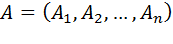который называется вектором направляющих косинусов вектора  (он имеет то же направление, что и вектор  и длину, равную 1), и вектора, составленного из частных производных функции f (x). Этот вектор называется градиентом функции и имеет обозначения 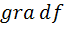или .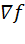

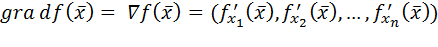
Формулу 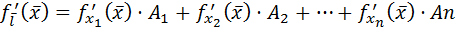 можно переписать в виде:

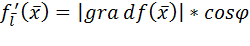
Из данной формулы следует, что максимальное по абсолютной величине значение производная по направлению приобретает при j = 0, т.е. когда направление, по которому берется производная, совпадает с направлением градиента; и производная по направлению равна нулю, когда ее направление ортогонально направлению градиента.

Таким образом, градиент направлен в сторону наибольшего возрастания функции и ортогонален поверхности уровня в каждой точке.