Понятие функции нескольких переменных.

Множество всевозможных упорядоченных наборов действительных чисел ( 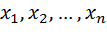) называется n-мерным координатным пространством и обозначается 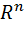. Если задана прямоугольная система координат с началом в точке О, то говорят о декартовой системе координат.

При n=2 множество 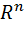 =  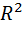называют координатной плоскостью, а координаты точки М обозначают соответственно х и у. Если на координатной плоскости выбрана ортогональная система координат с началом в точке О (0,0), то говорят, что задана плоскость хОу.

Аналогично при n = 3 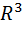 называют координатным пространством, а его точки обозначают как M (x, y, z).

Расстоянием между точками 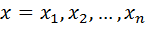 и и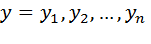з пространства  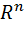назовем величину:

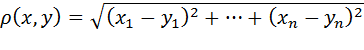
Для всякого положительного числа e (e > 0) назовем e - окрестностью точки 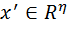множество всех точек 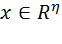, удовлетворяющих неравенству  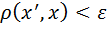и обозначим V (x¢).

Проколотой e -окрестностью точки x ¢ назовем множество точек х, удовлетворяющих условию 0 < r(x ¢, x) < e . На плоскости e - окрестностью точки М ( 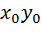) будет внутренность круга с центром в точке М( 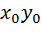) радиуса e.

Точка 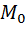 называется внутренней точкой множества 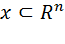, если существует e -окрестность точки 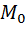, целиком содержащаяся в Х.

Точка 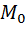 называется внешней точкой множества 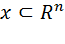, если существует e -окрестность точки 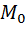, целиком выходящая за пределы Х.

Точка 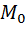 называется граничной точкой множества Х, если любая e - окрестность точки  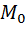содержит как точки множества Х, так и точки, ему не принадлежащие.

Множество Х называется открытым, если все его точки являются внутренними.

Множество Х называется замкнутым, если оно содержит все свои граничные точки.

Множество Х называется выпуклым, если отрезок, соединяющий пару любых точек множества, целиком содержится в этом множестве.

Рассмотрим n-мерное координатное пространство 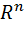 . Пусть X – некоторое множество в 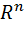. Если каждой точке 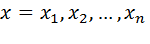из множества X соответствует одно вполне определенное значение переменной величины zÎR, то говорят, что z есть функция n независимых переменных и пишут  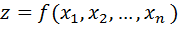или z=f(x). Множество X называют областью определения функции.

Будем считать далее, что n = 2, при этом большая часть понятий переносится и на случай n > 2. Если множество X задано на плоскости (n = 2), то пишут z = f(x,y).

Открытое связное множество будем называть открытой областью, а открытую область вместе с ее границей – замкнутой областью. Всякая область может быть задана с помощью одного или нескольких неравенств.

Линией уровня функции двух переменных z = f (x, y) называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и то же и равно C.

Предел и непрерывность.

Число А называется пределом функции z = f (x,y) при 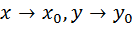(или в точке 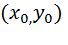если для любого числа e > 0, найдется число d > 0, такое, что для всех точек (х, y), отличных от 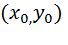и отстоящих от точки 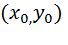на расстояние r меньшее, чем d (т.е. при 0 < r < d ), выполняется неравенство

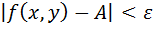
Обозначается предел так:

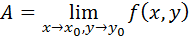
Теорема:

Если пределы в правых частях представленных ниже равенств существуют, то существуют пределы и в левых частях, при этом

]

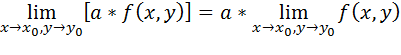
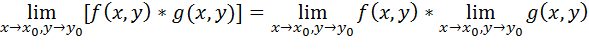
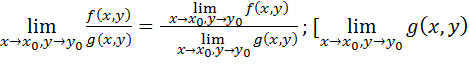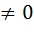
Функция z = f (x, y) называется непрерывной в точке 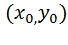, если она:

1) определена в точке ,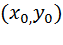

2) имеет конечный предел при ;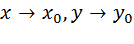

3) этот предел равен значению функции в точке 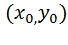,= т.е

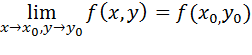, иными словами, функция непрерывна в точке 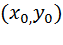, если для каждого положительного числа e существует такое положительное число d , что для всех точек (х, у) таких, что  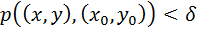, выполняется неравенство

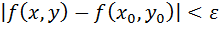
Геометрический смысл непрерывности очевиден: график в точке 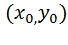, представляет собой сплошную поверхность.

Справедлива следующая теорема о непрерывности сложной функции нескольких переменных.

Теорема:

Пусть функции u (x, y), v (x, y) непрерывны в точке 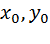, а функция z=f (u,v) непрерывна в точк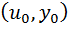е  , где 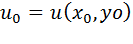. Тогда сложная функция 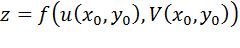непрерывна в точке ).

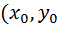Этот результат распространяется и на случай произвольного n числа переменных. Функция двух переменных непрерывна на некотором множестве точек D, если она непрерывна в каждой точке этого множества.

Для функции, непрерывной на ограниченном замкнутом множестве, справедливы теоремы, аналогичные теоремам Вейерштраса для функций одной переменной. Именно функция, ограниченная на указанном множестве, достигает своего наибольшего и наименьшего значений и принимает хотя бы по одному разу каждое значение, заключенное между наименьшим и наибольшим значениями на этом множестве, включая их самих.

Если в какой-либо точке области определения функции двух переменных не выполнено хотя бы одно из трех условий непрерывности, то эта точка является точкой разрыва.

Например, функция 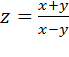 не определена при x = y. Эти точки – точки разрыва данной функции, они заполняют прямую y = x.