Универсальная тригонометрическая подстановка Интеграл вида 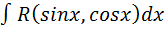 , где R – рациональная функция от  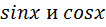рационализируется универсальной подстановкой:

,

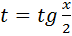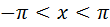
В этом случае:

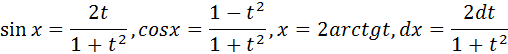
Подстановка называется универсальной, так как она позволяет рационализировать любой интеграл вида .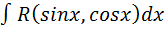

Пример: найти: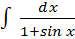

Применяя универсальную подстановку 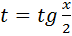, получаем:

:

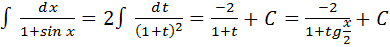
Частные тригонометрические подстановки.

Рассмотрим интегралы 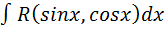, где R – рациональная функция. В отдельных случаях вместо универсальной тригонометрической подстановки удобно применять частные тригонометрические подстановки. Рассмотрим некоторые из них.

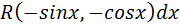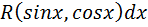1. Если имеет место тождество  º , то интеграл  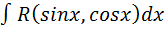рационализируется подстановкой:

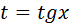
Тогда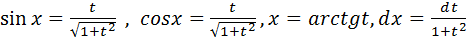

Интегралы вида 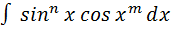,  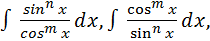где n и m – натуральные числа, удобнее вычислять с помощью метода замены переменной. В зависимости от четности n и m употребляют следующие варианты:

1) n – четное, m – нечетное, подстановка: t = ;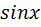

2) n – нечетное, m – четное, подстановка: t = ;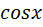

3) m и n – оба нечетные, любая из двух подстановок: 1 или 2 (если m < n, то 2, а если n < m, то 1);

4) m и n – оба четные, тогда следует понизить степень тригонометрических функций и в полученной сумме проверить каждое слагаемое по п.п. 1–3.

Интегрирование иррациональных функций.

Рассмотрим случаи, в которых замена переменной позволяет свести интегралы от иррациональных функций к интегралам от рациональных функций, т.е. рационализировать интеграл.

Обозначим через 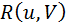функцию от переменных u,V и некоторых постоянных, которая построена с использованием лишь четырех арифметических действий (сложение, вычитание, умножение и деление).

Например, .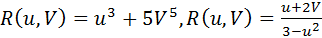

1. Интегралы вида 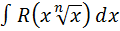, где , рационализируется заменой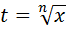

2. Интегралы вида 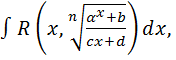где , ad-cb≠0, рационализируются

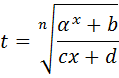
3. Интегралы вида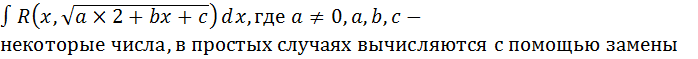

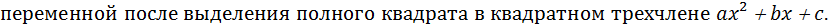
Интегрирование иррациональностей с помощью тригонометрических подстановок.

Интегралы вида 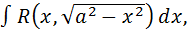 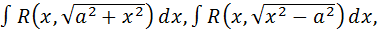  рационализируются с помощью подстановок:

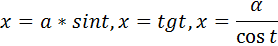
Пример: найти: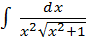

Положим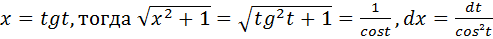

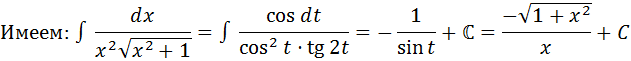
Так как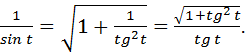

Интегрирование рациональных функций.

Рациональной называется функция, которую можно представить в виде дроби 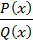, где P(x) и Q(x) – многочлены.

Если степень многочлена в числителе равна или больше степени многочлена в знаменателе, то, выполнив деление, получим:

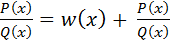, где W(x) – некоторый многочлен, а R(x) – многочлен степени ниже, чем Q(x).

Теорема:

Если рациональная функция 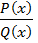имеет степень многочлена в числителе меньше степени многочлена в знаменателе, а многочлен Q(x) представлен в виде

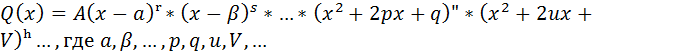- действительные числа, А – коэффициент при старшей степени многочлена Q(x), а квадратные трехчлены не имеют действительных корней, тогда данную функцию можно единственным образом представить в ви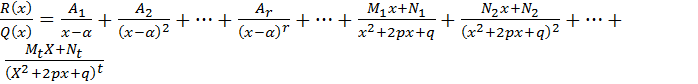де:

, где 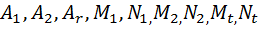 - некоторые действительные числа.

Заметим, что разложение 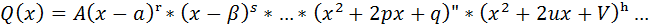 всегда возможно (по основной теореме алгебры), если степень многочлена Q(x) выше второй.

Выражение 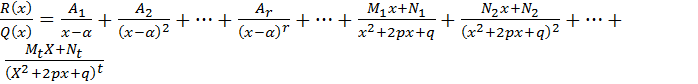называется разложением рациональной функции на элементарные дроби. Равенство 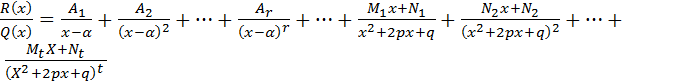имеет место для всех x, не являющихся действительными корнями многочлена Q(x).

Чтобы определить числа 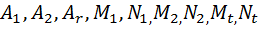умножим обе части разложения

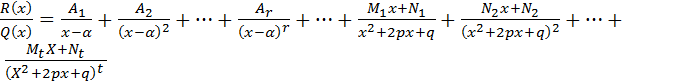 на Q(x). Поскольку равенство между многочленом R(x) и многочленом, который получится в правой части, должно быть справедливо для всех x, то коэффициенты, стоящие при равных степенях x, должны быть равны между собой. Приравнивая их, получаем систему уравнений первой степени, из которой найдем неизвестные числа .

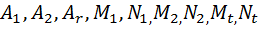Такой метод отыскания коэффициентов разложения рациональной функции называется методом неопределенных коэффициентов.