Неопределённый интеграл. Таблица.
Функция F(x) называется первообразной для функции f(x) (на некотором промежутке Х), если для всех значений x из этого промежутка выполняется равенство F¢(x) = f (x).
Теорема.
Если F(x) – первообразная для функции f(x), то любая другая первообразная для функции f(x) может быть представлена в виде F(x) + C, где C – произвольная постоянная.
Пример 1. Для функции f(x) = x семейство первообразных выглядит следующим образом: 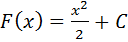 , так как
, так как 
Если функция F(x) – первообразная для функции f(x), то множество функций F(x) + C, где C – произвольная постоянная, называется неопределенным интегралом от функции f(x) и обозначается
ò f ( x ) dx = F ( x ) + C
при этом функция f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением, а переменная x – переменной интегрирования.
Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.
Интегрирование представляет собой операцию, обратную дифференцированию.
Пример 2.
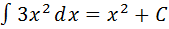 , так как
, так как 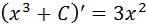
Основные свойства неопределенного интеграла:
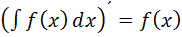
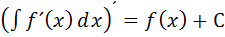
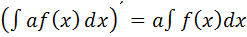
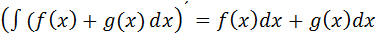
Таблица:
1. 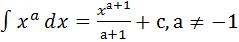 , x>0 (ln x)´=
, x>0 (ln x)´=  , x<0 (ln (-x))´=
, x<0 (ln (-x))´= 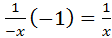
2. 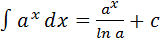 , a>0 and a≠1
, a>0 and a≠1
3. 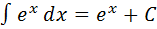
4. 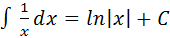
5. 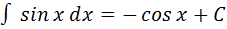
6. 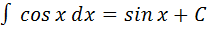
7. 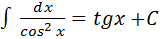
8. 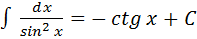
9. 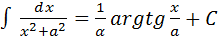
10. 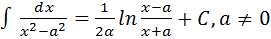
11. 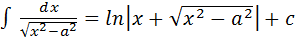 , a≠0
, a≠0
12. 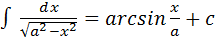 ,
, 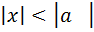
13. 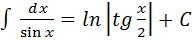
14. 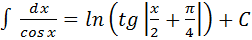
15. 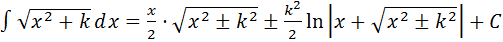
Метод подведения под знак дифференциала.
Пусть требуется вычислить 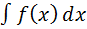 .
.
Предположим, что существует дифференциальная функция 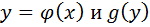 . Такие, что f(x)=g(φ(x)
. Такие, что f(x)=g(φ(x) 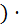 φ´(x).
φ´(x).
Тогда 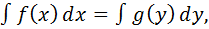 где
где 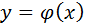 , то есть вычисление интеграла
, то есть вычисление интеграла 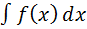 сводится к вычислению интеграла
сводится к вычислению интеграла 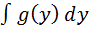 , которое может оказаться проще исходного и послед. постановке y=φ(x).
, которое может оказаться проще исходного и послед. постановке y=φ(x).
Пример: найти: 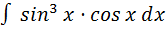
Если 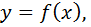 то
то 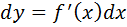
Если 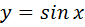 , то
, то 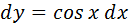
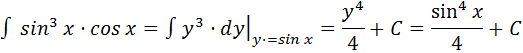
Метод подстановки
Теорема.
Пусть функция x =j(t) определена и дифференцируема на некотором промежутке T и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве T справедлива формула
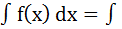 [j(t)]×j¢(t)dt - называется формулой замены переменной в неопределенном интеграле.
[j(t)]×j¢(t)dt - называется формулой замены переменной в неопределенном интеграле.
Пример: найти: 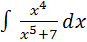
Положим 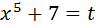 , тогда
, тогда 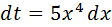 .
.
Получаем
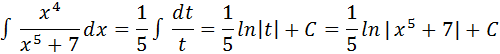
Теорема.
Пусть F(x) – некоторая первообразная для функции f(x). Тогда
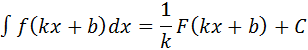
где k и b – некоторые числа, k ¹ 0.
Пример: найти: 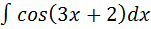
В данном случае k=3, b=2, тогда получаем

Интегрирование по частям.
Пусть функции u(x) и V(x) определены и дифференцируемы на некотором промежутке Х и пусть функция u¢(x)V(x) имеет первообразную на этом промежутке. Тогда на промежутке Х функция u(x)V¢(x) также имеет первообразную и справедлива формула:
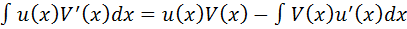 - называется формулой интегрирования по частям в неопределенном интеграле.
- называется формулой интегрирования по частям в неопределенном интеграле.
Так как 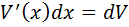 ,
, 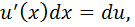 то ее можно записать в виде:
то ее можно записать в виде:
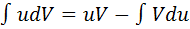
Эта формула позволяет свести вычисление 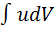 к вычислению интеграла
к вычислению интеграла 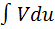 , который может оказаться более простым.
, который может оказаться более простым.
Замечание 1. В качестве V можно взять любую функцию F(x) + C, где C – постоянная. Удобно взять V = F(x), т.е. C = 0.
Замечание 2. Формулу интегрирования по частям можно применять несколько раз, причем иногда получая не сразу готовый ответ, а так называемые рекуррентные соотношения.
Замечание 3. При разбиении подынтегрального выражения на сомножители в качестве u удобно выбирать ту часть выражения, которая упростится после дифференцирования, с учетом того, чтобы оставшаяся часть dv подынтегрального выражения достаточно легко интегрировалась.
Например, в качестве u удобно выбрать многочлен P(x), если он сочетается с легко интегрируемыми функциями типа экспоненты ( 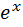 ), синуса или косинуса, а если в подынтегральном выражении присутствуют неудобные для интегрирования функции типа lnx или arctgx, то в качестве dV удобно выбрать именно эти выражения.
), синуса или косинуса, а если в подынтегральном выражении присутствуют неудобные для интегрирования функции типа lnx или arctgx, то в качестве dV удобно выбрать именно эти выражения.
Пример: найти: 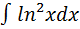
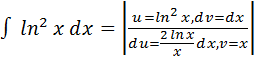 =
= 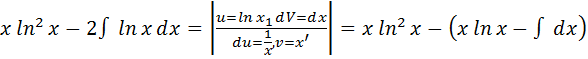 =
= 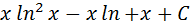
Теорема:
Если рациональная функция 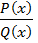 имеет степень многочлена в числителе меньше степени многочлена в знаменателе, а многочлен Q(x) представлен в виде
имеет степень многочлена в числителе меньше степени многочлена в знаменателе, а многочлен Q(x) представлен в виде
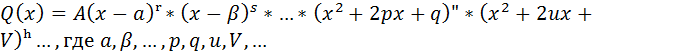 - действительные числа, А – коэффициент при старшей степени многочлена Q(x), а квадратные трехчлены не имеют действительных корней, тогда данную функцию можно единственным образом представить в виде:
- действительные числа, А – коэффициент при старшей степени многочлена Q(x), а квадратные трехчлены не имеют действительных корней, тогда данную функцию можно единственным образом представить в виде:
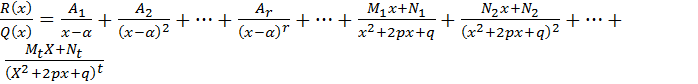 , где
, где 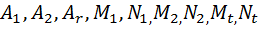 - некоторые действительные числа.
- некоторые действительные числа.
Заметим, что разложение 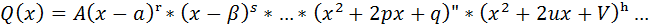 всегда возможно (по основной теореме алгебры), если степень многочлена Q(x) выше второй.
всегда возможно (по основной теореме алгебры), если степень многочлена Q(x) выше второй.
Выражение 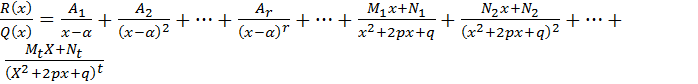 называется разложением рациональной функции на элементарные дроби. Равенство
называется разложением рациональной функции на элементарные дроби. Равенство 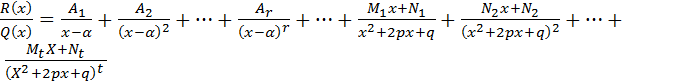 имеет место для всех x, не являющихся действительными корнями многочлена Q(x).
имеет место для всех x, не являющихся действительными корнями многочлена Q(x).
Чтобы определить числа 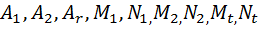 умножим обе части разложения
умножим обе части разложения
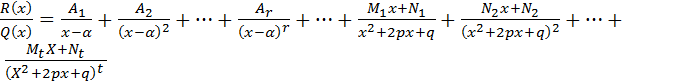 на Q(x). Поскольку равенство между многочленом R(x) и многочленом, который получится в правой части, должно быть справедливо для всех x, то коэффициенты, стоящие при равных степенях x, должны быть равны между собой. Приравнивая их, получаем систему уравнений первой степени, из которой найдем неизвестные числа
на Q(x). Поскольку равенство между многочленом R(x) и многочленом, который получится в правой части, должно быть справедливо для всех x, то коэффициенты, стоящие при равных степенях x, должны быть равны между собой. Приравнивая их, получаем систему уравнений первой степени, из которой найдем неизвестные числа 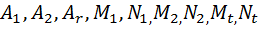 .
.
Такой метод отыскания коэффициентов разложения рациональной функции называется методом неопределенных коэффициентов.
Условный экстремум.
Пусть в области n D Ì R определена функция 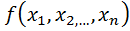 и система функций
и система функций 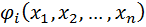 ,
, 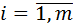 и пусть множество
и пусть множество 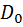 является областью допустимых значений системы уравнений
является областью допустимых значений системы уравнений
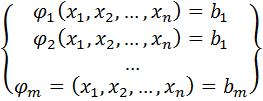
Задача нахождения условного экстремума ставится следующим образом. Найти локальный экстремум функции 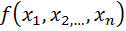 на множестве
на множестве 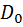 , или, другими словами, найти:
, или, другими словами, найти:
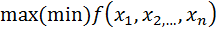
при ограничениях, заданных уравнениями связи (системы).
Для нахождения условного экстремума вводится функция Лагранжа:
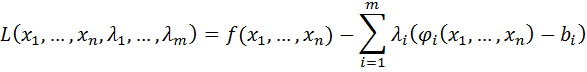
где 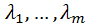 – множители Лагранжа. Если ввести вектора
– множители Лагранжа. Если ввести вектора 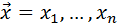 ,
, 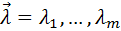 ,
, 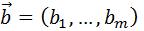 и вектор-функцию
и вектор-функцию 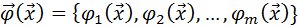 , то функцию Лагранжа можно записать следующим образом:
, то функцию Лагранжа можно записать следующим образом:
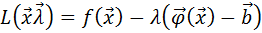
Теорема:
Предположим, что в точке 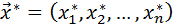 функция
функция 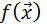 имеет условный локальный экстремум, ранг матрицы
имеет условный локальный экстремум, ранг матрицы
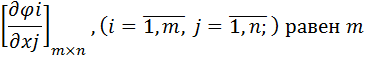
 Тогда точка (
Тогда точка ( 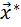 ,
, 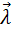 ) является стационарной точкой функции Лагранжа, и необходимые условия экстремума запишутся в виде:
) является стационарной точкой функции Лагранжа, и необходимые условия экстремума запишутся в виде:
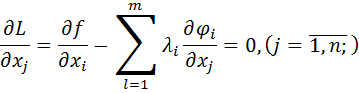
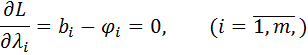
Существуют также и достаточные условия, при выполнении которых решение системы данных уравнений определяет точку экстремума функции 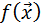 . Этот вопрос решается на основании исследования знака второго дифференциала функции Лагранжа. Однако достаточные условия представляют главным образом теоретическое значение.
. Этот вопрос решается на основании исследования знака второго дифференциала функции Лагранжа. Однако достаточные условия представляют главным образом теоретическое значение.
Метод наименьших квадратов.
В прикладных задачах экономики, физики, техники зависимость между переменными x и y часто выражается в виде таблиц, где значения переменных получены в результате эксперимента или являются статистическими данными за ряд лет. Для изучения связи между этими переменными часто требуется выразить зависимость между этими переменными аналитически, т.е. в виде некоторой формулы.
Вообще говоря, задача восстановления функции по конечному числу ее значений математически неразрешима. Поэтому ставится задача приближенно заменить табличную функцию некоторой формулой так, чтобы ее значения возможно мало отличались от табличных. Такая формула, полученная на основе экспериментальных данных, называется эмпирической.
Построение эмпирической формулы по собранным экспериментальным данным состоит из двух этапов: 1) подбор вида этой формулы, зависящей от параметров; 2) определение по некоторому критерию этих параметров.
Во многих случаях характер зависимости между переменными предполагается известным из каких-либо теоретических соображений, т.е. остается только определить параметры этой формулы. Обычно для экономических исследований достаточно одной из шести следующих формул:
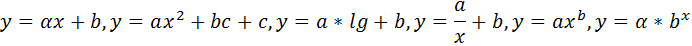
Наибольший интерес представляют две первые эмпирические формулы. Допустим, что опытным (эмпирическим) путем определены значения двух переменных x и y.
| X | 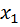
| 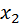
| 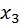
| … | 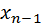
| 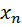
|
| y | 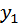
| 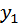
| 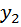
| … | 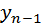
| 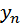
|
Требуется выразить зависимость между x и y в виде уравнения y = f (x).
Предположим, что первый этап завершен – вид функции установлен. Тогда переходят ко второму этапу – определению неизвестных параметров.
Согласно наиболее распространенному методу наименьших квадратов в качестве неизвестных параметров функции f (x) выбирают такие значения, чтобы сумма квадратов отклонений «теоретических» значений 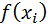 , найденных по эмпирической формуле y = f (x), от соответствующих опытных значений
, найденных по эмпирической формуле y = f (x), от соответствующих опытных значений 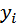 была минимальной:
была минимальной:
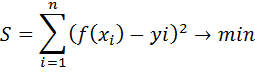
Пусть в качестве функции y = f (x) взята линейная функция y = ax + b и задача сводится к отысканию таких значений a и b, при которых функция
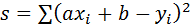
примет наименьшее значение. Заметим, что функция S = S(a, b) функция двух переменных a и b до тех пор, пока мы не нашли, а затем не зафиксировали их “наилучшие” (в смысле метода наименьших квадратов) значения, а 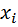 и
и 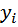 – постоянные числа, найденные экспериментально.
– постоянные числа, найденные экспериментально.
Таким образам, для нахождения прямой, наилучшим образом согласованной с опытными данными, достаточно решить систему:
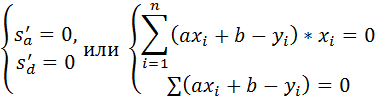
Эта система имеет единственное решение, так как ее определитель не равен нулю (что легко проверить). Найденные значения a и b дают функции S(a,b) минимум.
По лекции:
Пусть требуется установить зависимость между двумя величинами x и y, для которых известны несколько предыдущих измерений, записанных в таблицу (зависимости прибыли у от месяца х)
| Х | 
| 
| … 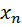
|
| у | 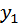
| 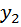
| … 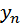
|
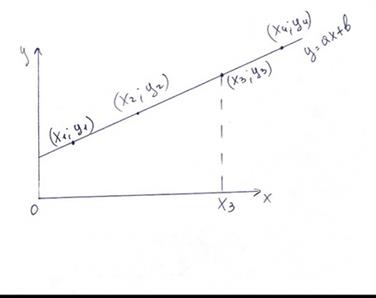
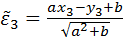
Если эти точки лежат близко к некоторой прямой, то для прогнозирования дальнейшего изменения у(х) ищут прямую y=ax+b, наименее удаленную от этих точек.
Рассмотрим 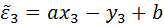
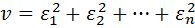
Если 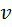 будет min при некоторых значениях a и b, то говорят, что прямая найдена по методу наименьших квадратов.
будет min при некоторых значениях a и b, то говорят, что прямая найдена по методу наименьших квадратов.
Формула наименьших квадратов:
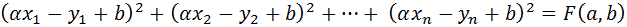
Неизвестны: a и b
Известны: x и y
Дифференцируем
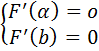
Получаем:
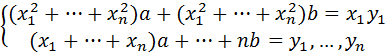
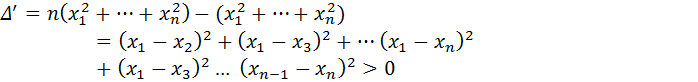
Неопределённый интеграл. Таблица.
Функция F(x) называется первообразной для функции f(x) (на некотором промежутке Х), если для всех значений x из этого промежутка выполняется равенство F¢(x) = f (x).
Теорема.
Если F(x) – первообразная для функции f(x), то любая другая первообразная для функции f(x) может быть представлена в виде F(x) + C, где C – произвольная постоянная.
Пример 1. Для функции f(x) = x семейство первообразных выглядит следующим образом: 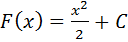 , так как
, так как 
Если функция F(x) – первообразная для функции f(x), то множество функций F(x) + C, где C – произвольная постоянная, называется неопределенным интегралом от функции f(x) и обозначается
ò f ( x ) dx = F ( x ) + C
при этом функция f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением, а переменная x – переменной интегрирования.
Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.
Интегрирование представляет собой операцию, обратную дифференцированию.
Пример 2.
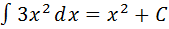 , так как
, так как 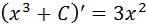
Основные свойства неопределенного интеграла:
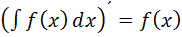
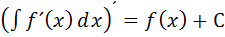
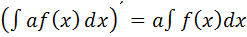
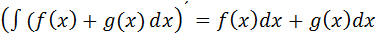
Таблица:
1. 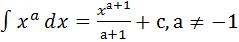 , x>0 (ln x)´=
, x>0 (ln x)´=  , x<0 (ln (-x))´=
, x<0 (ln (-x))´= 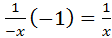
2. 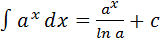 , a>0 and a≠1
, a>0 and a≠1
3. 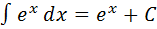
4. 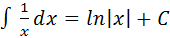
5. 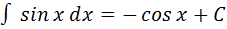
6. 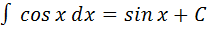
7. 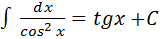
8. 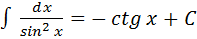
9. 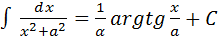
10. 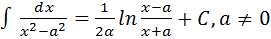
11. 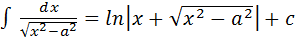 , a≠0
, a≠0
12. 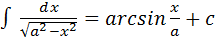 ,
, 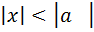
13. 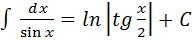
14. 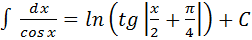
15. 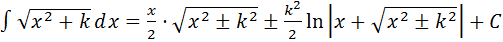
Метод подведения под знак дифференциала.
Пусть требуется вычислить 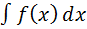 .
.
Предположим, что существует дифференциальная функция 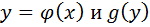 . Такие, что f(x)=g(φ(x)
. Такие, что f(x)=g(φ(x)  φ´(x).
φ´(x).
Тогда 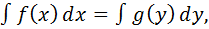 где
где 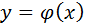 , то есть вычисление интеграла
, то есть вычисление интеграла 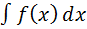 сводится к вычислению интеграла
сводится к вычислению интеграла 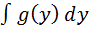 , которое может оказаться проще исходного и послед. постановке y=φ(x).
, которое может оказаться проще исходного и послед. постановке y=φ(x).
Пример: найти: 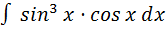
Если 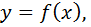 то
то 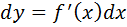
Если 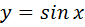 , то
, то 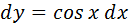
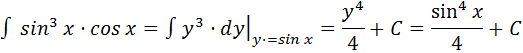
Метод подстановки
Теорема.
Пусть функция x =j(t) определена и дифференцируема на некотором промежутке T и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве T справедлива формула
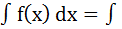 [j(t)]×j¢(t)dt - называется формулой замены переменной в неопределенном интеграле.
[j(t)]×j¢(t)dt - называется формулой замены переменной в неопределенном интеграле.
Пример: найти: 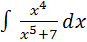
Положим 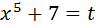 , тогда
, тогда 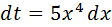 .
.
Получаем
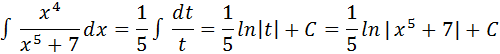
Теорема.
Пусть F(x) – некоторая первообразная для функции f(x). Тогда
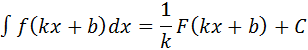
где k и b – некоторые числа, k ¹ 0.
Пример: найти: 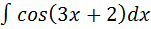
В данном случае k=3, b=2, тогда получаем

Интегрирование по частям.
Пусть функции u(x) и V(x) определены и дифференцируемы на некотором промежутке Х и пусть функция u¢(x)V(x) имеет первообразную на этом промежутке. Тогда на промежутке Х функция u(x)V¢(x) также имеет первообразную и справедлива формула:
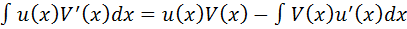 - называется формулой интегрирования по частям в неопределенном интеграле.
- называется формулой интегрирования по частям в неопределенном интеграле.
Так как 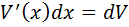 ,
, 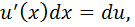 то ее можно записать в виде:
то ее можно записать в виде:
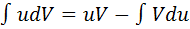
Эта формула позволяет свести вычисление 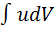 к вычислению интеграла
к вычислению интеграла 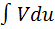 , который может оказаться более простым.
, который может оказаться более простым.
Замечание 1. В качестве V можно взять любую функцию F(x) + C, где C – постоянная. Удобно взять V = F(x), т.е. C = 0.
Замечание 2. Формулу интегрирования по частям можно применять несколько раз, причем иногда получая не сразу готовый ответ, а так называемые рекуррентные соотношения.
Замечание 3. При разбиении подынтегрального выражения на сомножители в качестве u удобно выбирать ту часть выражения, которая упростится после дифференцирования, с учетом того, чтобы оставшаяся часть dv подынтегрального выражения достаточно легко интегрировалась.
Например, в качестве u удобно выбрать многочлен P(x), если он сочетается с легко интегрируемыми функциями типа экспоненты ( 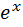 ), синуса или косинуса, а если в подынтегральном выражении присутствуют неудобные для интегрирования функции типа lnx или arctgx, то в качестве dV удобно выбрать именно эти выражения.
), синуса или косинуса, а если в подынтегральном выражении присутствуют неудобные для интегрирования функции типа lnx или arctgx, то в качестве dV удобно выбрать именно эти выражения.
Пример: найти: 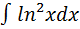
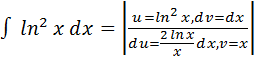 =
= 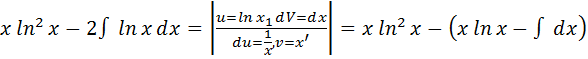 =
= 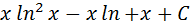
Дата: 2019-11-01, просмотров: 296.