| xi | 2 | 6 | 8 | 12 | 16 | 21 | 24 | S |
| f i | 1 | 2 | 3 | 6 | 4 | 3 | 1 | 20 |
| pi | 0,05 | 0,10 | 0,15 | 0,30 | 0,20 | 0,15 | 0,05 | 1,00 |
| p%i | 5 | 10 | 15 | 30 | 20 | 15 | 5 | 100 |
| Fi | 1 | 3 | 6 | 12 | 16 | 19 | 20 | |
| Pi | 0,05 | 0,15 | 0,30 | 0,60 | 0,80 | 0,95 | 1,00 | |
| P%i | 5 | 15 | 30 | 60 | 80 | 95 | 100 |
На практике исследователь пользуется какой-либо одной частотой (при необходимости — несколькими). Какие именно частоты выбрать для построения вариационного ряда и отражения распределения значений признака в данной группе испытуемых выбирает сам исследователь, руководствуясь удобством работы. Однако можно сформулировать некоторые рекомендации:
- Если выборка небольшого объема, то можно использовать абсолютные частоты. При увеличении объема выборки, целесообразнее перейти к относительным или процентным частотам.
- Если в исследовании сравнивается несколько выборок разного объема (имеют разное количество испытуемых), то вариационные ряды рекомендуется строить на основе относительных или процентных частот, так как использование абсолютных частот может привести к ложным выводам. Например, если абсолютная частота для какого значения в выборке из 20 человек равна 5, а в выборке из 25 человек для этого значения она тоже равна 5, то мы не можем сделать вывод об одинаковой встречаемости этого значения в обеих выборках, потому что 5/20 ¹ 5/25.
- В шкале наименований чаще всего используют процентные частоты.
Различают простой вариационный ряд (например, таблица 2) и более сложный вариационный ряд — сгруппированное распределение. Сгруппированное распределение — это вариационный ряд, в котором шкала значений признака разделена на интервалы (группы значений, разряды) и для этих интервалов подсчитаны частоты. Такой вариационный ряд используется, если измерительная шкала признака является достаточно длинной, например, возраст испытуемых, интеллект и т.п.
Графический способ состоит в наглядном отражении результатов исследования. При этом исследователь может решать две задачи: 1) продемонстрировать выраженность признака в данной выборке испытуемых; 2) продемонстрировать выраженность и изменчивость признака в данной выборке (одновременно).
Для решения первой задачи строится профиль, отражающий среднюю выраженность данных признаков (как правило, это делается в пределах одной методики) в выборке испытуемых (или выборках). Такой профиль строится по средним арифметическим оценкам (см. ниже описание параметров распределений). Пример профиля приводится на рисунке 1.
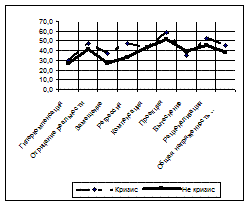
Рис. 2. Выраженность психологических защит
При построении подобных среднегрупповых профилей обратите внимание на «длину» шкал в данной методике (максимально возможный диапазон значений по шкале). К сожалению, во многих методиках эта «длина» различна. В этом случае график, построенный по средним арифметическим оценкам, рассчитанным по первичным данным, может приводить к ложной интерпретации результатов (например, одинаковые оценки в 5 баллов по двум шкалам, одна из которых имеет максимум в 10 баллов, а другая максимум — 15 баллов, не означает одинаковую выраженность свойства).
Для решения второй задачи строится график, отражающий выраженность и изменчивость признака одновременно. Этот график может быть построен на основе вариационных рядов графиков распределений, отражающих зависимость между значениями признака и мерой возможности их появления в выборке.
Существуют два типа графиков — график дифференциального распределения и график интегрального распределения. Первый из них строится по частотам f I; pi; p%i; второй — по накопленным частотам Fi; Pi или P%i. По оси абсцисс откладываются значения признака, по оси ординат — частоты.
Каждый из графиков может быть трех видов:
А) если точки соединяются прямой линией, то график носит название полигон частот или многоугольник частот (рис. 3);
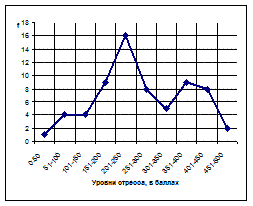
Рис. 3. Многоугольник частот дифференциального распределения
Б) если точки соединяются плавной кривой, апроксимирующей многоугольник частот, то график носит название кривая распределения;
В) если частоты отражаются в виде столбика, то график называется гистограмма или столбиковая диаграмма (рис.4).
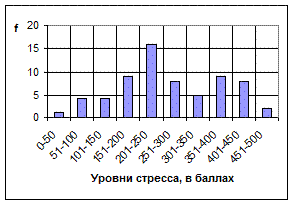
Рис. 4. Гистограмма дифференциального распределения
В шкале наименований часто используется еще один вид графиков — круговая диаграмма — круг, в котором площадь сектора пропорциональна процентной или относительной частоте (рис.5).
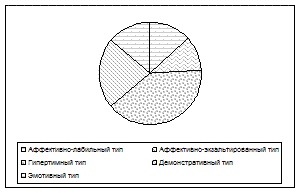
Рис. 5. Круговая диаграмма представленности в выборке типов акцентуаций
Дата: 2019-11-01, просмотров: 344.