Почти любая наука в процессе своего развития приходит к измерениям. Измерение можно рассматривать как построение своеобразной функциональной зависимости, в которой аргументами являются реальные величины (измеряемые объекты), а функциями — обозначающие их числа, меры. Причем функции должны обладать одним свойством — аддитивностью, то есть любые сложные преобразования реальных величин должны однозначно соответствовать операциям с их мерами (числами) и наоборот. Следовательно, 1) для измерения не обязательно нужно знать абсолютное значение величин, достаточно уметь определять их относительное изменение; 2) изучаемые явления вообще могут не характеризоваться определенными реальными величинами, их отношения и изменения должны носить определенный и сопоставимый характер — и они могут быть измерены; 3) измерение можно производить разнообразными способами; единственное условие, которое необходимо строго соблюдать — аддитивность[1] принятой функции меры в соответствии с правилами измерения.

Измерение — приписывание числовых форм объектам или событиям в соответствии с определенными правилами (Стивенс, 1960 г.).

На рисунке 1 приведена схема, в которой отражены типы измерений, методы, которыми они выполняются, и измерительные шкалы, получаемые при использовании этих методов.

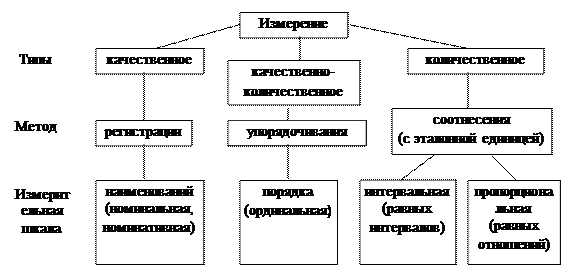
Рис.1. Типы измерений и измерительные шкалы

При измерении методом регистрации правила измерения таковы, что они позволяют лишь установить, что один объект отличается по измеряемому свойству от другого объекта, у которого измеряемое свойство качественно иное. Поэтому в результате объекты классифицируются по группам (классам), которые могут быть обозначены номерами, названиями, именами и т.п. Обозначение класса не измеряется количественно, оно лишь позволяет отличить один объект от другого в отношении измеряемого свойства. Это и составляет сущность шкалы наименований (синонимы — номинальная шкала, номинативная шкала).

Безразлично, в каком порядке будут расположены классификационные ячейки (названия групп). То, что номер одного класса больше или меньше другого, ещё ничего не говорит о свойствах объектов, за исключением того, что они различаются.

Единицей измерения, которой мы оперируем, является количество объ­ектов, принадлежа­щих данному классу, (испытуемых, ре­акций лю­дей, выборов и т.п.), или часто­та (абсолютная частота), относительная частота (частость, вероятность), процентная частота. С числами, получаемыми в результате измерения методом регистрации, нельзя производить арифметические операции.

Примеры шкалы наименований: пол, национальность, семейное положение, образование, здоровый – больной, клинические диагнозы, левша – правша, тип темперамента, тип личности и т.п.

При измерении методом упорядочивания правила измерения таковы, что мы уже можем сравнить объекты по принципу «больше — меньше измеряемого свойства», однако, сколько именно этого свойства невозможно установить. Классификационные ячейки образуют последовательность от ячейки "самое малое значе­ние" до ячейки "самое большое значение" (или наоборот). Должно быть не меньше трёх классификационных ячеек. Измерительная шкала, полученная таким образом, называется шкалой порядка (или ординальной шкалой).

Единицей измерения является расстояние в один класс, или один ранг, или один балл. При этом расстояние между рангами (баллами) может быть разным (оно нам неизвестно).

С числами, получаемыми методом упорядочивания, уже можно производить арифметические операции. Однако интерпретация результатов этих арифметических действий должна быть осторожной, потому что эти числа обладают следующим свойствами. Значения чисел, присваивае­мых объектам, отражают коли­чество свойства, принадлежа­щего объектам. Однако равные разно­сти чисел не означают равных разностей в количествах свойств.

Примеры шкалы порядка: твердость минералов; оценка успеваемости; любые первичные оценки в психологических методиках.

При измерении методом соотнесения правила измерения таковы, что существует четко описанная единица измерения, с которой сравниваются измеряемые объекты. Число, получающееся в результате измерения методом соотнесения, указывает, сколько эталонных единиц данного свойства находится в измеряемом объекте. При измерении методом соотнесения возможно получение двух измерительных шкал, которые сконструированы по-разному: равных интервалов и равных отношений.

Шкалы классифицируют объекты по принципу «больше на … единиц — меньше на … единиц». Каждое из возможных значений признака (расстояние между числами в шкале) отстоит от другого на равном расстоянии — одна единица измерения. В этих шкалах равные разности чисел, присвоенных объектам, отражают равные различия в количествах измеряемого свойства. С числами, полученными методом соотнесения, уже можно производить любые арифметические операции.

В шкале равных интервалов (интервальной шкале) нулевая точка шкалы произвольна и не указывает на отсутствие измеряемого свойства.

Примеры интервальных шкал: календарное время, шкала температур по Цельсию, шкала температур по Фаренгейту; в психологических измерениях сюда относятся так называемые квазиинтервальные (искусственно созданные) шкалы, ими являются любые стандартизованные шкалы[2] в психологических методиках (например, шкала IQ, стены, Т-баллы, стенайны, стандартная 20-балльная шкала в субтестах теста Векслера и любые другие стандартизованные оценки в методиках).

В шкале равных отношений (пропорциональной шкале) объекты классифицируются пропорционально степени выраженности измеряемого свойства. Отношения чисел, присвоенных в измерении, отражают количественные отношения измеряемого свойства. На шкале существует абсолютный нуль. Значение нуль означает отсутствие измеряемого свойства.

Примеры пропорциональных шкал: расстояние, длина отрезков или физических объектов, время, температура по Кельвину (абсолютный нуль); в психологии — шкалы порогов абсолютной чувствительности, время реакции, количество объектов или субъектов (абсолютный нуль).

Результаты, полученные тем или иным методом измерения, допускают различные математические процедуры. Обработка этих результатов зависит от того, по какой шкале были измерены психологические признаки. Поэтому прежде чем приступать к обработке и выбору процедур математико-статистического анализа данных, необходимо ответить себе на вопрос — по какой шкале были измерены данные признаки.