Репрезентация экспериментальных данных. Упорядочивание. Табулирование. Сгруппированные данные. Наглядное представление данных измерения. Достоинства и недостатки различных способов графического представления данных. Общие советы при построении графиков.

Основные понятия математической статистики: случайное событие, вариация, частота, вероятность, распределение вероятности, выборка, генеральная совокупность, вариационный ряд, полигон частот, гистограмма, кривая распределения. Характеристики статистических совокупностей: меры положения, меры изменчивости, меры связи. Меры возможной ошибки. Виды распределений, важные для психологии.

Методические рекомендации к изучению темы

       При изучении темы 2 следует обратить особое внимание на различные способы репрезентации результатов исследования и их возможности. Обратите внимание на возможные ошибки при построении графиков. Внимательно прочитайте советы при построении графиков, изложенные в книге Гласса и Стенли. Наиболее сложным для восприятия в данной теме является алгоритм построения сгруппированного распределения. Поэтому рекомендуется не просто прочитать предлагаемый пример его построения, а решить его самостоятельно. Таблица «Общий обзор параметров распределений» очень важна в практической работе, так как она помогает выбирать параметры, уместные в данном исследовании. Её необходимо выучить наизусть.

После изучения материала лекции ответьте на контрольные вопросы, ответы занесите в конспект.

Материалы лекции.

Итак, математическая статистика — это математический аппарат, разработанный для анализа случайных событий.

Случайное событие — событие, которое в основных условиях иногда происходит, а иногда нет, и при этом в каждый данный момент невозможно предугадать произойдет событие или нет.

Случайная величина — переменная, которая может принимать значения из определенного множества чисел в зависимости от появления случайного события.

Вариация x_i — отдельное значение случайной величины. В исходную матрицу первичных данных записываются вариации по каждому признаку.

Описать результаты, полученные в исследовании, можно тремя способами:

• табличным,

• графическим и

• параметрическим.

Табличный способ представления результатов исследования состоит в составлении вариационных рядов. Вариационный ряд — это таблица, в которой указываются меры возможности появлений значений признака. На практике исследователи редко представляют вариационные ряды в своих отчетах или публикациях. Однако они являются очень важными, поскольку на их основе рассчитываются параметры распределений.

К мерам возможности появлений значений признака относятся две группы значений:

I. Дифференциальные меры:

f _i— абсолютная частота;

p_i — относительная частота (частость, вероятность);

p_%i — процентная частота;

II. Интегральные меры:

F_i — накопленная абсолютная частота;

P_i — накопленная относительная частота;

P_%i — накопленная процентная частота.

Абсолютная частота f _i — это количество испытуемых (или случаев), которые имеют какое-то данное значение признака. Она определяется путем подсчета испытуемых с каким-то определенным значением признака на основе исходной матрицы первичных данных.

Относительная частота (частость, приближенная оценка вероятности) p_i рассчитывается по следующей формуле: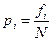

Процентная частота p_%i находится по формуле: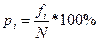

Эти три вида частот (абсолютная, относительная и процентная) могут рассчитываться для признаков, измеренных по любой шкале (наименований, порядка, интервальной и пропорциональной).

Накопленные частоты являются мерами изменчивости в шкалах порядка, интервальной и пропорциональной (в шкале наименований их подсчитать невозможно). Они отвечают на вопрос, сколько испытуемых в выборке (или какая ее часть) имеют какое-то значение признака x_i и меньше чем это значение. Для того чтобы ее найти, необходимо в упорядоченном (значения признака расположены по возрастанию) вариационном ряду, начиная с ячейки с наименьшим значением, отвечать себе на вопрос: сколько человек в выборке имеют данное значение x_i и меньше чем это значение. В последней ячейке вариационного ряда, соответствующей максимальному значению, должен получиться общий объем выборки (или 1,00[3] для относительных частот, или 100% для процентных частот).

Накопленная абсолютная частота F_i находится по абсолютным частотам; накопленная относительная частота P_i — по относительным; накопленная процентная частота P_%i — по процентным частотам.

Например, опишем экспериментальные данные — результаты измерения экстраверсии с помощью опросника Айзенка в группе из 20 человек будут представлены в таблице 2.

В приведенном примере (таблица 2) является вариационным рядом, в котором в качестве иллюстрации посчитаны все виды частот.

Таблица 2