Общий вид итеративной циклической структуры с предусловием while … endможно представить следующим образом:

W hile ЛогическоеВыражение

…

Операторы

…

End

Отличительной особенностью этой структуры является то, что Операторы, расположенные в теле структуры, выполняются только в том случае, если
ЛогическоеВыражение равно – % T(True). Как только ЛогическоеВыражение становится % F(False), происходит выход из структуры повторения, и управление передается на инструкцию, расположенную после ключевого слова end.

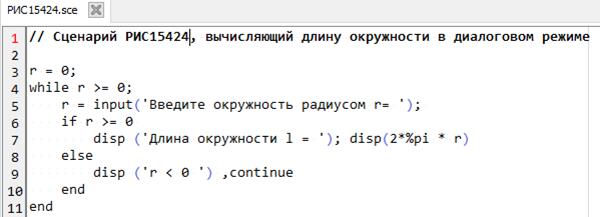
Рассмотрим простой пример вычисления длины окружности.
Сценарий, сохраненный в файле с именем РИС15424, служит для многократного вычисления длины окружности по вводимому пользователем значению радиуса r, где диалог реализован с помощью командыinput и disp. Cтроки, связанные с вводом переменной r и вычислением длины окружности, включены в управляющую структуру while ... end. Это необходимо для циклического повторения вычислений при вводе различных значений r. Пока r >0, цикл повторяется. Но стоит задать r <0, вычисление длины окружности перестает выполняться, а цикл завершается. Поскольку во второй строке программы величина r определена равной 0, цикл выполняется хотя бы один раз.

--> //Загрузка сценария РИС15424и его выполнение --> -->clear -->exec('РИС15424.sce');  Введите окружность радиусом r=4  Длина окружности l =25.132741  Введите окружность радиусом r=-1 r<0

Рис. 1.5.4-24 Сценарий, использующий операторы
итеративной циклической структуры

При организации цикла с предусловием блоки тела цикла, следующие за блоком, в котором проверяется условие выхода из цикла, выполняются всякий раз, когда логическое выражение принимает значение True. При первом невыполнении этого условия происходит выход из цикла. Таким образом, возможен случай, когда тело цикла не будет выполнено ни разу.

При вычислении значений функций или числовых последовательностей (например, арифметической прогрессии), их часто записывают в виде специальных сумм или произведений, называемых рядами. Вычисление суммы членов ряда проводится с использованием итерационных циклических алгоритмов, которые позволяют вычислять приближенное значение результата с заданной точностью. При этом для вычисления отдельных слагаемых (или сомножителей), как правило, используются рекуррентные формулы.

Рекуррентная формула – это такая формула, которая позволяет вычислить значение n-го члена последовательности, используя значение одного или нескольких предыдущих членов этой последовательности.

Рассмотрим некоторую последовательность, содержащую бесконечное число членов: a ₀ , a ₁ , a ₂ , a ₃ ,…, a_i ,…, a_n ,… В таких задачах требуется вычислять члены последовательности до тех пор, пока очередной вычисленный член не будет удовлетворять некоторому условию.

Если задано некоторое число ε, условия окончания итерационного процесса могут, например, быть следующими:

a_n < ε– для убывающей последовательности;

a_n > ε– для возрастающей последовательности;

| a_n |< ε– для убывающей знакопеременной последовательности;

| a_{n +1} - a_n |< ε – для некоторых других типов последовательностей.