Выщелачивания мышьяка

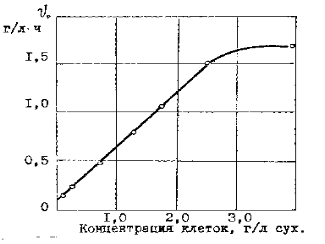
Рисунок 8

Таким образом, использование уравнений (21 ) и ( 24 ) для описания кинетических кривых возможно только до концентрации биомассы 2,5 г/л по сухому весу, поскольку в них входит величина

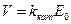 ( 27 )

где, 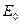 – концентрация «фермента» ( пропорциональна концентрации биомассы),

 k_кат – каталитическая константа

Применяя интегральный метод анализа с использованием уравнения ( 27) кинетики бактериального окисления сульфидных минералов в медно-цинковых и мышьяковистых концентратах было показано, что кинетика бактериальных окислительных процессов подчиняется уравнениям ферментативного катализа ( рисунок 9 и 10 ). Определенные кажущие величины констант К_м = - 22 г/л и V_max = -0,15 г/л ч имеют отрицательное значение,

Кинетика выщелачивания цинка из медно-цинкового концентрата

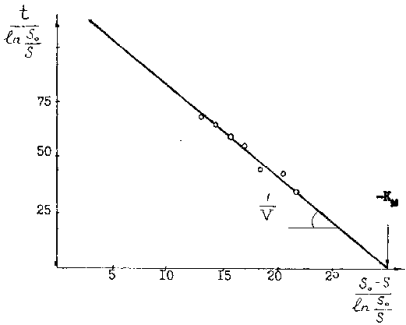
Рисунок 9

 что свидетельствует о наличии сильного конкурентного ингибирования ферментативной реакции продуктами выщелачивания (ионами железа, меди, цинка или мышьяка). В этом случае из одной кинетической кривой определить константы невозможно. Поэтому пользуются полными кинетическими кривыми для различных концентраций субстрата.

Кинетика выщелачивания сульфидного мышьяка из золотомышьякового концентрата с использованием биомассы обычной плотности

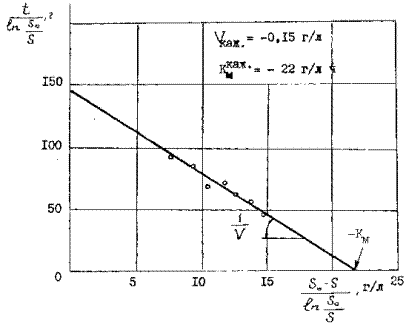
Рисунок 10

Явление конкурентного ингибирования в ферментативном катализе имеет место в случает закрепления ингибитора на активный цент фермента ( конкуренция за активный центр). При этом константа Михаэлиса увеличивается, а максимальная скорость реакции не изменяется. Конкурентное ингибирование продуктом реакции вызвано связыванием фермента продуктом или продуктами реакции Р в непродуктивный комплекс ЕР и может быть представлено в виде трехстадийной схемы

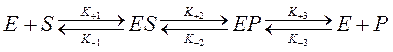              (28)

Дифференциальное уравнение скорости реакции по схеме ( 28 )можно представить в виде:

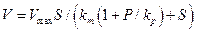                                                                    ( 29 )

Для необратимых реакций при бактериальном окислении сульфидов когда k_-2→ 0, константа Михаэлиса k_m = k_-1 k₊₃ + k₊₂ k₊₃ / ( k₊₁ k₊₂ + k₊₃ ), а константа ингибирования

k_р + k₊₃/ k_-3. Величина константы ингибирования характеризует сродство продукта к ферменту. Форма уравнения ( 29 ) аналогична ( 21 ) , поэтому по одной кинетической кривой нельзя определить замедление реакции по времени в результате накопления продукта окисления или истощением исходного субстрата.

Интегрируя (29 ), а затем линеаризуя, получим уравнение:

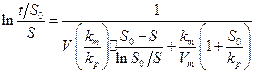                                                                          ( 30 )

которое выражается прямой линией в координатах  ,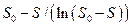  

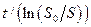
Действительно, при бактериальном окислении сульфидного мышьяка в мышьяксодержащем концентрате неадаптированной к мышьяку культурой А.ferrooxidans этот процесс хорошо описывается интегральным уравнением ферментативной кинетики с конкурентным ингибированием продуктом реакции ( 29 ). При этом на оси абсцисс отсекается отрезок, равный 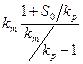, а наклон прямых к оси абсцисс
равен tgφ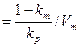  

Отрицательное значение тангенса угла наклона характерно для случая k_m