Идеальный газ можно описать тремя основными макропараметрами: давлением, температурой и объемом. Все эти величины объединяет уравнение состояния, которые практически одновременно открыли два ученых, поэтому данный закон носит название уравнения Менделеева-Клапейрона:
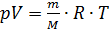 ,
,
p – давление идеального газа,
V – объем идеального газа,
m – масса газа,
M – молярная масса газа,
R – универсальная газовая постоянная, 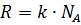 (k – постоянная Больцмана, NA – число Авогадро), R=8,31 Дж/(моль×К)
(k – постоянная Больцмана, NA – число Авогадро), R=8,31 Дж/(моль×К)
T – абсолютная температура идеального газа.
Все структурные единицы газа находятся в постоянном и непрерывном движении, поэтому все они обладают кинетической энергией. Сумма кинетических энергий всех структурных единиц - внутренняя энергия газа. Так как энергия одной структурной единицы вещества определяется по формуле: 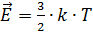 , а таких единиц N:
, а таких единиц N: 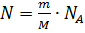 . То внутренняя энергия идеального одноатомного газа равна:
. То внутренняя энергия идеального одноатомного газа равна: 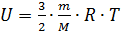
Не сложно заметить, что данная формула похожа на правую часть уравнения Менделеева-Клапейрона. Поэтому можно сделать вывод, что найти внутреннюю энергию структурной единицы можно и по следующей формуле: 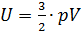 . Данные уравнения соответствуют одноатомному газу.
. Данные уравнения соответствуют одноатомному газу.
Если газ двухатомный, то внутренняя энергия равна: 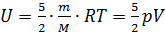 . Общий вид внутренней энергии:
. Общий вид внутренней энергии: 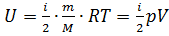
Закон Дальтона для давления смеси разреженных газов
Очень редко в реальном мире можно встретить газ, состоящий только из одного компонента. Наиболее популярны смеси газов. Так как мы знаем, что газы имеют свойство занимать весь представленный объем, то для каждого из газов в смеси объем будет тот же, но концентрация будет меняться в зависимости от количества структурных единиц: 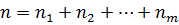 . Если подставить общую концентрацию в уравнение для определения давления, то получим:
. Если подставить общую концентрацию в уравнение для определения давления, то получим:
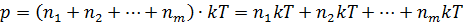
Из этого можно сделать вывод, что общее давление всех газов равно сумме давлений каждого из них. Каждое давление по отдельности называется парциальным: 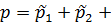 …+
…+ 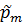 .
.
Изопроцессы.
Любое вещество характеризуют макро- и микропараметры. Если говорить о макропараметрах, то для перехода системы из одного состояния в другое обязательно должны изменяться минимум две величины. Это значит, что отдельно только давление, только объем или только температура не может изменяться. Они либо изменяются все согласно уравнению Клапейрона, либо изменяется две величины.
Уравнение Клапейрона : 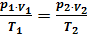
Изопроцессы - это процессы, во время которых масса газа и один макропараметр остаются неизменными. Существует три основных изопроцесса: изобарный, изохорный, изотермический.
Изобарный процесс. Изолированным, неизменным остается давление. Если в уравнении Клапейрона давление остается неизменным, то оно сокращается и можно получить новый закон - данному процессу соответствует закон Гей-Люссака: 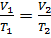 .
.
Можно заметить, что если некоторый газ нагреть, то он начнет расширяться, то есть увеличивать свой объем. То есть при увеличении одной величины должна увеличиваться и другая. Данный закон имеет прямую зависимость переменных величин.
Данному процессу соответствуют следующие графики (изобары):
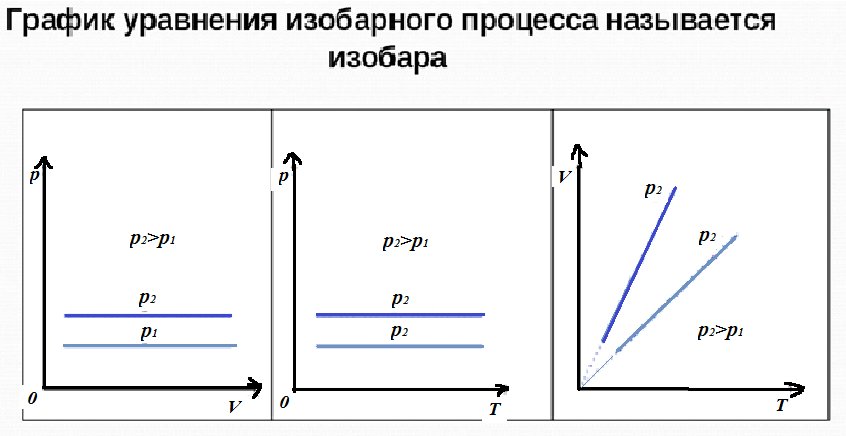
Расположение прямой на графике зависит от значения давления. Чем выше давление, тем выше график зависимости. Обратите внимание на то, что график в координатах VT не начинается с нуля - это говорит о том, что науке не известны еще случаи достижения абсолютного нуля. Если бы график начинался бы с нуля, это говорило бы о том, что объем равен нулю. Но если это так, то частиц газа нет, и значит, при отсутствии частиц просто не может идти речь о температуре. Более того, в законе Гей-Люссака температура находится в знаменателе, а, как мы знаем, знаменатель не может быть равен нулю.
Изохорный процесс. Во время данного процесса изменяется только давление и температура, а объем остается неизменным. При данных условиях из уравнения Клапейрона получим закон Шарля: для газа данной массы отношение давления газа к его термодинамической температуре постоянно: 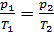 . Здесь прослеживается та же зависимость - при увеличении одного параметра должен увеличиваться и другой. Данному процессу соответствуют аналогичные графики (изохоры):
. Здесь прослеживается та же зависимость - при увеличении одного параметра должен увеличиваться и другой. Данному процессу соответствуют аналогичные графики (изохоры):
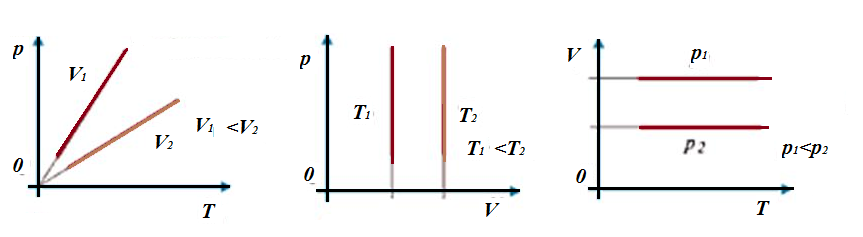
Изотермический процесс. При данном процессе изменяется давление и объем. Процесс описывает закон Бойля-Мариотта: 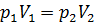 .
.
Обратим внимание, это единственный процесс, где наблюдается обратная зависимость - при увеличении одного параметра, второй должен падать. Графики данного процесса называются изотермами.
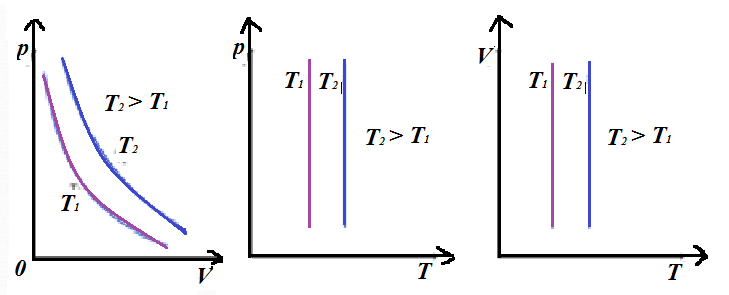
Дата: 2019-07-31, просмотров: 313.