Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Сорбция – это процесс поглощения твердым телом или жидкостью веществ из окружающей среды. Для тонких полимерных пленок интересен вопрос поглощения именно низкомолекулярных веществ (НМВ), что обусловлено областью их применения.

Сорбция включается в себя адсорбцию (поглощение на поверхности) и абсорбцию (объемное поглощение). Первый процесс является превалирующим при развернутой поверхности полимеров и их малом термодинамическом сродстве (способности к взаимному растворению, или совместимости) с низкомолекулярными веществами. Во всех других случаях превалирует растворимость, или абсорбция.[5]

Адсорбция газов и паров

Адсорбция – это явление самопроизвольного концентрирования молекул одного вещества (адсорбата) на границе раздела фаз с другим веществом (адсорбентом). Происходит это вследствие уменьшения свободной поверхностной энергии в поверхностном слое (на границе раздела фаз) по сравнению с ее значением в объеме фазы. Адсорбционное уравнение Гиббса описывает это явление:

 

где 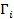 – избыток i-го компонента (адсорбата) в поверхностном слое; dμ_i  - изменение химического потенциала (парциальной мольной свободной энергии) i-го компонента при адсорбции;  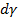– изменение свободной поверхностной энергии.

Данное уравнение выводится из обобщенного уравнения Гиббса-Дюгема для многокомпонентных гетерогенных систем (объемных фаз). Нас же интересует случай, когда количество компонентов системы ограничивается двумя. [5]Тогда уравнении Гиббса записывается в виде:

где 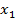и 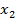 - мольные доли компонентов.

Величины 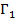 и 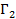 зависят от выбора разделяющей поверхности на границе раздела фаз. Общее изменение удельной свободной поверхностной энергии при адсорбции называется поверхностным давлением  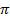и представляет из себя разность энергий до и после адсорбции (2.3).

 

При контакте поверхности полимеров с газами или парами низкомолекулярных летучих веществ при заданных Т и р (газообразное состояние низкомолекулярного вещества соответствует температуре, существенно выше Т_кип, а парообразное – ниже Т_кип) основным процессом является сорбция, включающая абсорбцию (растворимость) низкомолекулярного вещества в объеме и его адсорбцию на поверхности полимера. При неразвитой поверхности полимеров и их близком сродстве к низкомолекулярным веществам, что проявляется, в первую очередь, в случае паров органических веществ или воды и близких к ним по полярности полимеров, превалирующую роль играет абсорбция (растворимость) (см. ниже Раздел 2.2).

При развернутой поверхности полимеров и их малом сродстве к низкомолекулярным веществам, в частности, в случае инертных газов и слаборастворимых паров, определяющее значение имеет адсорбция. При этом за разделяющую поверхность принимается поверхность твердой (полимерной) фазы, а величина адсорбции оценивается количеством молекул газа или пара, связанным с этой поверхностью. [5]

При низком давлении газа или пара изменение химического потенциала адсорбируемого вещества (адсорбата или компонента 1):

где 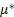 - стандартный химический потенциал;  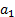– активность, равная давлению адсорбируемого газа при его низких значениях или, в случае пара, отношению давления пара к давлению насыщения.

 В данном случае адсорбционное уравнение Гиббса (2.1) может быт записано в виде:

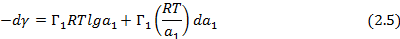
Таким образом,  избыток адсорбата (компонента 1) может быть рассчитан по изменению поверхностной энергии при различной активности пара или различном давлении газа.

В соответствие с молекулярно-кинетической теорией адсорбции (теорией Лэнгмюра) адсорбция инертных газов с очень слабым (дисперсионным) межмолекулярным взаимодействием на твердых поверхностях, в том числе полимерных, содержащих равномерно распределенные активные центры со сферой действия, распространяющейся на одну адсорбируемую молекулу, адсорбция рассматривается как процесс установления равновесия адсорбция-десорбция, т.е. равенства скоростей конденсации молекул на активных центрах и их отрыва (испарения) с образованием некоторого равновесного адсорбционного слоя [3].

В изобарно-изотермических условиях кинетика насыщения адсорбционного слоя имеет вид, показанный на рисунке 2.1.1:

Г(t)

Г∞

t

 

Рисунок 2.1.1 Схема кинетики образования равновесного насыщенного (мономолекулярного) адсорбционного слоя [5].

где Г(∞) – масса молекул в адсорбционном слое, или равновесная адсорбция.

При заданном давлении адсорбция инертных газов сравнительно слабо зависит от температуры в соответствие с уравнением Клапейрона-Клаузиуса (2.6) из-за малых значений энтальпии (теплового эффекта) адсорбции ΔН_а, но сильно зависит от давления при заданной температуре.

В изотермических условиях с увеличением давления газа, в пределе, образуется насыщенный мономолекулярный адсорбционный слой, т.е. достигается максимальная равновесная адсорбция 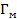. Схематически вид изотермы адсорбции Лэнгмюра в координатах Г(∞)-р показан на рисунке 2.1.2, кривая 1.

 

p

Гм

Г∞(p)

(1)

(2)

 

Рисунок 2.1.2 Схема изотермы адсорбции Лэнгмюра (1) и БЭТ (2) [5].

Изотерма Лэнгмюра описывается уравнением:

где коэффициент b характеризует отношение констант скоростей процессов десорбции и адсорбции молекул.

Если адсорбция газов на твердой поверхности определяется Ван-дер-ваальсовскими силами, радиус действия которых больше размеров адсорбируемых молекул, то адсорбция не ограничивается мономолекулярным слоем и при высоком давлении приводит к образованию полимолекулярного слоя. Теоретически изотерма полимолекулярной адсорбции, проявляющейся в случае слаборастворимых (инертных) газов и паров на развернутой поверхности полимеров описывается уравнением Брунауэра-Эммета-Тейлора (БЭТ) [5]: 

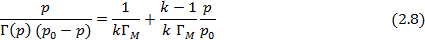
где 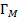 – величина адсорбции при образовании мономолекулярного слоя,  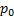–давление насыщенного пара,  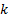– коэффициент, учитывающий разницу между теплотой адсорбции до образования монослоя и теплотой конденсации при образовании полимолекулярного слоя.

Примерами такой адсорбции является адсорбция слабополярных газов или паров неполярных жидкостей на поверхности полярных полимеров и наоборот, сильнополярных газов или паров полярных жидкостей на поверхности неполярных полимеров,

Такая изотерма имеет так называемый S-образный вид и схематически показана на рисунке 2.1.2, кривая 2. При этом адсорбция при заданном давлении более сильно зависит от температуры по сравнению с Лэнгмюровской вследствие больших значений энтальпии адсорбции.

На практике экспериментальное определение изотерм адсорбции инертных газов или паров на поверхности полимеров используется, главным образом, для определения их удельной поверхности, т.е. площади поверхности, приходящейся на единицу массы полимера, по величине адсорбции в мономолекулярном слое 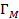 (в молях газа или пара на 1 г полимера):

где 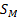 - площадь, занимаемая одной молекулой,  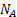– число Авогадро.

Если изотерма подчиняется уравнению Лэнгмюра, то Г_м определяется непосредственно по предельной величине адсорбции, а если уравнению БЭТ – то расчетом по параметрам прямой, полученной перестройкой изотермы в координатах .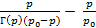

Равновесная абсорбция

Сорбция (поглощение) низкомолекулярных веществ (газов и паров) полимерами включает в себя адсорбцию на поверхности и объемное поглощение (абсорбцию, или растворимость). Первый процесс является превалирующим при развернутой поверхности полимеров и их малом термодинамическом сродстве с низкомолекулярными веществами, и о нем говорилось в разделе 2.1. Во всех других случаях превалирует абсорбция (растворимость), но ее обычно называют просто сорбцией. При этом поглощаемое вещество называется сорбатом, а поглощающее – сорбентом.

Мерой термодинамического сродства (способности к взаимному растворению, или совместимости) органических полимеров между собой и с другими веществами, в том числе газами, парами и жидкостями в изобарно-изотермических равновесных условиях, служит разность свободных энергий взаимодействующих компонентов в отдельности в двух случаях:

1) в свободном состоянии

2)  в молекулярной смеси (растворе) [5]

Это так называемая свободная энергия смешения :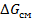

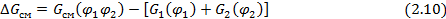
где 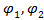  – объемные доли компонентов (1 – низкомолекулярный компонент - жидкость, пар или газ; 2 – полимер); 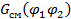, , 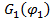 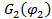– свободные энергии смеси и отдельных компонентов соответственно.

При этом 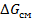 определяется энтальпией ( 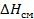) и энтропией ( 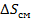) смешения:

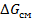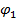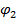Условиями термодинамической совместимости (растворимости) компонентов при любом их соотношении при заданных условиях являются: отрицательное значение  и вогнутость кривой ее зависимости от  и . Определение пределов совместимости используется для получения обобщенных диаграмм фазовых состояний смесей компонентов [5].

Для оценки равновесной растворимости одного из компонентов в другом используется разность парциальной мольной свободной энергии (химического потенциала) соответствующего компонента в свободном состоянии и в растворе. В соответствие с теорией Флори-Хаггинса-Скотта для растворов линейных полимеров в низкомолекулярных веществах, изменение химического потенциала низкомолекулярного компонента (газа, пара или жидкости,), растворенного в полимере, по сравнению со свободным состоянием 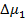 описывается уравнением:

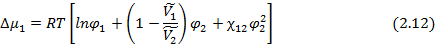
где 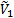 и 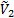 - парциальные мольные объемы низкомолекулярного вещества и полимера соответственно;  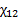- параметр взаимодействия полимер- низкомолекулярное вещество (параметр Флори-Хаггинса).

В этом уравнении два первых члена в скобках соответствуют энтропийному, а третий член – энергетическому (энтальпийному) вкладу вследствие перемешивания молекул компонентов и изменения их межмолекулярного взаимодействия при перемешивании соответственно. Отношение 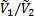 примерно равно степени полимеризации полимера x₂ и, следовательно, для высокомолекулярных полимеров и низкомолекулярных веществ обратное отношение 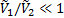. Параметр Флори-Хаггинса, характеризующий различие в энергии межмолекулярного взаимодействия компонентов в свободном конденсированном состоянии (11, 22) и в растворе (12). В случае идеальных растворов, для которых эти взаимодействия равны, 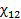=1/2, а в случае реальных растворов  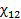описывается уравнением Гильдебранда[5]:

 где 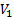 - мольный объем низкомолекулярного вещества, 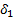,  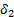– параметры растворимости компонентов.

Для газов и паров изменение химического потенциала:

где а₁ – активность, равная для паров отношению давления пара к давлению насыщенного пара, для жидкостей – единице, для газов при сравнительно небольших давлениях – давлению газа.

При этом уравнение Флори-Хаггинса-Скотта (2.12) для линейных полимеров может быть записано в следующем виде:

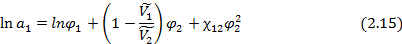
откуда при 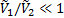 можно получить выражение для равновесной объемной доли сорбированного низкомолекулярного вещества:

При φ₂→1, т.е. если сорбция сравнительно невелика  (φ₁ << φ₂), это выражение упрощается:

Из этих соотношений следует, что чем больше разность параметров растворимости сорбата и полимера, т.е. чем больше их параметр взаимодействия, тем меньше количество равновесно сорбируемого линейным полимером низкомолекулярного вещества. [5]

В случае сетчатых полимеров помимо чисто термодинамических вкладов (энтропийного и энергетического) в изменение свободной энергии и химического потенциала низкомолекулярного вещества при его сорбции существенный вклад вносит упругое сопротивление полимерной сетки увеличению объема полимера при сорбции низкомолекулярного вещества. Учет этого эффекта позволяет записать уравнение Флори-Хаггинса-Скотта ( 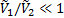) в виде уравнения Флори-Ренера:

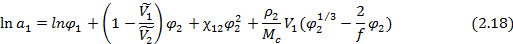
где 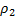 – плотность исходного полимера,  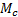–средняя молекулярная масса полимерных цепей между узами сетки (отношение  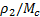 характеризует густоту сетки , или частоту ее узлов и равно числу молей цепей между узлами сетки в единице объема полимера 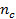); f – функциональность полимерной сетки, равная числу цепей, сходящихся в одном узле (чаще всего равная 3 ил 4).

Для равновесной объемной доли сорбированного низкомолекулярного вещества при этом получается выражение:

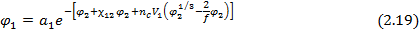
При φ₂→1, т.е. если сорбция сравнительно невелика  (φ₁ << φ₂) это выражение упрощается:

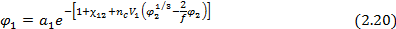
При этом необходимо помнить, что с термодинамической точки зрения жидкое состояние соответствует равенству единице активности ее паров, и в этом случае lna₁=0. Однако, очевидно, что сорбция паров при их активности, равной единице, т.е. при р=р_∞, и поглощение этого же вещества из жидкой фазы может существенно различаться из-за различия в процессах адсорбции паров на полимерах и смачивания полимеров жидкостями, предшествующих растворению низкомолекулярного вещества, а также процессами растворения (экстракции) низкомолекулярных примесей, содержащихся в полимерах, низкомолекулярной жидкости, что не может происходить в случае насыщенного пара при отсутствие его конденсации на полимере [5].

На практике равновесная сорбция обычно определяется в количестве граммов сорбированного вещества на 1 грамм исходного полимера (в массовой, или весовой концентрации сорбата m_1∞, г/г), которая может быть пересчитана в его объемную или мольную концентрацию (с_1∞, см³/см³ или С_1∞, моль/см³ соответственно), объемные (φ=V₁/V₁+V₂) и весовые, или массовые (g=G₁/G₁+G₂) доли компонентов, где V и G - объем и масса компонентов, через их исходные удельные объемы (v) или плотности (ρ), по следующим соотношениям (для нормальных условий):

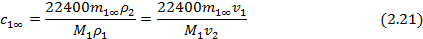
где М₁ и V₁ – молекулярная масса и мольный объем сорбата соответственно; 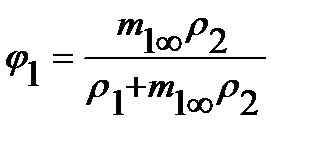; φ₂=1-φ₁; 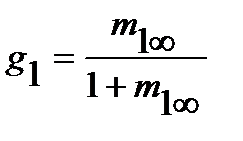; g₂=1-g₁.

При этом плотность сорбата, поглощаемого из газо- или парообразного состояния, соответствует плотности данного вещества в конденсированном жидком состоянии при заданной температуре [3].

На практике при оценке сорбции низкомолекулярных веществ полимерами, в первую очередь при поглощении жидкостей редкосетчатыми эластичными полимерами, большое значение имеет увеличение объема полимера, или его набухание, степень которого q характеризуется отношением объема полимера с сорбатом к его исходному объему. При аддитивности объемов сорбата и сорбента равновесная степень набухания в первом приближении равна: q= (V₁+V₂ )/V₂, т.е.q=1/ φ₂.

Зависимость количества сорбированного вещества от активности пара или давления газа при заданной температуре называется изотермой сорбции, которая в условиях термодинамического равновесия имеет, в соответствие с уравнениями Флори-Хаггинса-Скотта и Флори-Ренера, вид вогнутой кривой (Рисунок 2.2.1, кривая 1).

 

 

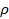m1∞

1

1

3

2

 

Рисунок 2.2.1 Изотермы сорбции паров растворителя аморфным полимером в исходном высоко-эластическом или вязко-текучем состоянии (1) и в исходном стеклообразном состоянии при его сохранении в процессе сорбции (2) и переходе в высоко-эластическое состояние с проявлением эффекта “отжига” (3). [5]

φ кр

φ 1

TC

Такое поведение характерно только для аморфных полимеров, находящихся в высокоэластическом или вязко-текучем состоянии, в которых возможно установление термодинамического равновесия. Для аморфных стеклообразных полимеров, находящихся при температуре ниже температуры стеклования (Т_с) в термодинамически неравновесном состоянии, установление такого состояния возможно только на той стадии сорбции растворителей и их паров, на которой произойдет переход полимера из стеклообразного в высокоэластическое состояние вследствие пластифицирующего эффекта, оказываемого низкомолекулярным сорбатом, т.е повышения молекулярной подвижности в полимере и, соответственно, понижения его Т_с ниже температуры эксперимента при Т_с1<Т_с2 (Рисунок 2.2.2) в соответствие с известным соотношением для Т_с двухкомпонентной системы полимер(2)-пластификатор(1): .

 

 

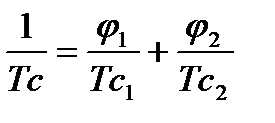Рисунок 2.2,2 Зависимости Т_с системы полимер-сорбат от объемной доли сорбата: при φ_{1 <} φ_кр полимер в условиях эксперимента находился в стеклообразном неравновесном состоянии, при φ_{1 >} φ_кр – в высоко-эластическом равновесном состоянии. [5]

 Если такой переход не происходит, т.е. в условиях, когда Т_с2 >Т_эксп, то полимер находится в неравновесном стеклообразном состоянии на всех стадиях сорбции. При этом условия установившейся сорбции, значительно меньшей по величине равновесной, соответствуют некоторому «квазиравновесному» состоянию полимер-сорбат, и, при отсутствии развернутой поверхности, сорбция протекает по механизму накопления молекул сорбата в «замороженном» свободном объеме полимера с их закреплением по активным центрам на начальных стадиях (при малой активности пара или малом давлении газа) и их агрегированием (кластеризацией) на конечных стадиях (при высокой активности пара или высоком давлении газа). В этом случае изотерма сорбции обычно S-образный вид, соответствующий изотерме адсорбции БЭТ (см. рис.2.1.2 и 2.2.1, кривые 2). [5]

При переходе аморфного, стеклообразного в исходном состоянии, полимера в высокоэластическое состояние в процессе сорбции ее изотерма должна сочетать характер изотермы БЭТ на начальных участках и изотермы Флори-Хаггинса-Скотта или Флори-Ренера – на конечных. При этом пластифицирующий эффект сорбата в полимере может оказывать эффект, аналогичный отжигу полимера и сопровождаться объемной усадкой полимера вследствие уменьшения «замороженного» свободного объема или дезориентацией, если предыстория полимера включала его закалку или эффекты ориентации соответственно. Все это должно резко проявиться на виде изотермы сорбции.

В случае аморфно-кристалличеких полимеров, сорбция паров и газов протекает преимущественно в аморфных областях, являющихся дефектными по сравнению с упорядоченными кристаллическими областями. Величина сорбции газов или паров такими полимерами может быть рассчитана через степень кристалличности (φ_кр):

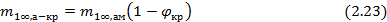
 Вид изотермы сорбции будет зависеть от реологического состояния аморфных областей (высокоэластического или стеклообразного) в исходном состоянии и от того, произойдет ли в процессе сорбции их переход из стеклообразного состояния, если они исходно находились в таком состоянии, в высокоэластическое или нет, аналогично некристаллизующимся полимерам. При переходе из стеклообразного состояния в высокоэластическое, помимо эффектов усадки свободного объема и дезориентации в аморфных областях, возможны также эффекты установления более равновесного состояния кристаллических областей, сопровождающихся увеличением степени кристалличности и даже перестройки структуры этих областей. Очевидно, что такие эффекты структурирования должны сказываться на характере изотермы сорбции на предельных стадиях [5].

При сорбции полимерами инертных газов часто наблюдается линейный вид изотермы, т.е проявляется прямая пропорциональность между количеством растворенного газа (в объемной концентрации с_1∞,см³/см³) и его давлением (закон Генри): m_1∞=σр или с_1∞=σр, где σ – константа уравнения Генри, или коэффициент растворимости (сорбции) с размерностью г/г атм или см³/см³атм соответственно. Пересчет σ из одной размерности в другую производится по формуле: σ[см³/см³атм]=22400σ[г/гатм]ρ₂/М₁ρ₁. Из термодинамического анализа растворимости низкомолекулярных веществ полимерами (см. уравнения Флори-Хаггинса-Скотта и Флори-Ренера) в случае равновесной сорбции газов линейными полимерами в высокоэластическом или вязко-текучем аморфном состоянии σ пропорционален еxp[-(1+χ₁₂)]. Зависимость равновесного коэффициента сорбции от температуры описывается уравнением Клапейрона-Клаузиуса через теплоту растворения:

Диффузия воды полимерами

        Сорбция и диффузия воды полимерами являются важнейшими характеристиками, в значительной мере определяющими их диэлектрические свойства и свойства на межфазных границах раздела слоев. Полимеры способны впитывать значительное количество воды, что в свою очередь отрицательно сказывается на, собственно, их диэлектрических свойствах. Особенно критично это для тонких полимерных пленок [6].

Диффузия – распространение вещества в какой-либо среде в направлении убывания его концентрации, обусловленная тепловым движением ионов, атомов и молекул. Для одномерной диффузии в идеальных растворах при отсутствии внешних сил справедлив первый закон Фика:

где 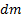 - масса вещества, переносимого при диффузии вдоль оси 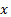за время 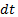сквозь площадку 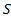, расположенную перпендикулярно к оси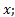 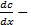градиент концентрации; 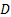-коэффициент диффузии.

Коэффициент диффузии имеет большое практическое значение, так как в значительной степени определяет скорость многих физико-химических процессов (адсорбции, десорбции и тд) [6].

Явления массопереноса вещества определяют важнейшие свойства полимеров, обусловленные взаимодействием полимера с веществом в объеме материала. Одним из основных механизмов переноса вещества в полимерах является диффузионный.

В зависимости от условий протекания этого процесса различают: взаимодиффузию (наблюдается при наличии градиента концентрации) и самодиффузию. Для описания процесса диффузии применяются два подходи: феноменологический и молекулярно-кинетический. Феноменологический подход основан на первом законе Фика. Поскольку поток вещества стремится устранить неравномерность распределения вещества в системе, то коэффициент диффузии является мерой скорости, с которой система способна при заданных условиях выравнивать разность с концентрацией. Эта скорость в свою очередь связана с микроскопическими параметрами системы, характеризующих тепловую подвижность макромолекул диффузионной среды и диффундирующих частиц температурой, структурой полимера и природой диффундирующего вещества[6].

Второе уравнение Фика, характеризующее нестационарный процесс диффузии, выражает изменение концентрации вещества в различных точках пространства как функцию времени:

Если диффузия протекает в трех направлениях изотропной среды:

В случае анизотропной среды перенос вещества в нестационарном состоянии описывается уравнением:

 

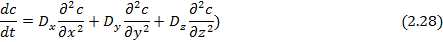
       Для расчета диффузии необходимо решить уравнения с определенными граничными условиями и начальными условиями, которые в свою очередь задаются параметрами исследуемого процесса.

При наличии макроскопических дефектов - трещин, пор, отверстий – в твердом теле мы имеем дело не с диффузионным межмолекулярным переносом, а с фазовым переносом, описываемым законом Пуазейля для газов и паров[5]. Деффекты рассматриваются в таком случае как трубки и капилляры. Как правило, данные дефекты наиболее ярко выражены в тонких пленках, и их наличие носит критический характер. Закон Пуазейля применяется в случае, когда длина пробега диффундирующего вещества меньше длины трубки. Тогда массоперенос можно оценить по закону Пуазейля:

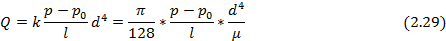
где 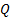 - объем газа, прошедшего за 1 секунду через сечение трубки; 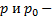давление в двух сечениях трубки;  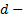диаметр трубки,  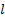- расстояние между сечениями;  - коэффициент вязкости.

В случае фазового переноса коэффициент диффузии имеет значения до 10^-3 до 10^-1 см²/с, в то время как коэффициент диффузии, описываемый законом Фика, имеет гораздо более низкие значения: от 10^-12 до 10^-6 см²/с. Таким образом, зная порядок значения коэффициента диффузии в системе, можно сделать вывод о характере процесса массопереноса.

Молекулярно-кинетический подход рассматривает диффузию как последовательность элементарных трансляционных движений молекул диффузанта в полимерной матрице. (т.н. диффузионный скачок) [6].