Для описания диэлектрических свойств вещества существует два подхода: феноменологический, который включает в себя описание макроскопических свойств и характеристик диэлектрика, и микроскопический, включающий описание свойств и явлений, протекающих в диэлектрике на атомно-молекулярном уровне [1]. Рассмотрим феноменологическую теорию полимерных диэлектриков.

Основные уравнения

       Рассмотрим связь между электрическим смещением D и напряженностью электрического поля в полимерном диэлектрике.

       Электрическое смещение в изотропной среде может быть представлено в виде:

       где 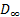 - электрическое смещение в диэлектрике, соответствующее случаю, когда частота электрических колебаний 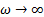;  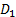– «диссипативная» часть электрического смещения.

       Электрическое смещение 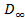 имеет вид, представленный в уравнении (1.15). Диссипативная же часть отличается от  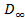только значением диэлектрической проницаемости диэлектрика, которое имеет значение для 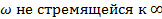, а имеющей конкретное значение.

       Представление электрического смещения в виде суммы двух членов является достаточно обоснованным, так как электрический момент диэлектрика, возникающий при наложении на него электрического поля, имеет две составляющие, одна из которых (деформационная) устанавливается очень быстро ( 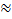10^-13 с.) [1]

       Следует заметить, что выражения для электрического смещения D типа ( 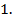15) справедливы лишь для стационарных электрических полей. Если электрическое поле Е, приложенное к диэлектрику, периодически изменяется во времени, то электрическое смещение в каждой точке среды в данный момент времени будет зависеть не только от напряженности электрического поля и скорости его изменения, но и от предыстории среды. Если время изменения электрического поля становится соизмеримым с временем установления статистического равновесия, то в среде активную роль будут играть релаксационные процессы. [1] Переход к равновесию может происходить таким образом, что будет иметь место суперпозиция релаксационных процессов. В связи с этим в реальном полимерном диэлектрике, находящимся в периодически изменяющемся электрическом поле, вектор электрического смещения должен каким-то образом учитывать предысторию среды.

       Поэтому при описании диэлектрических свойств полимерных диэлектриков должны использоваться некоторые неравновесные значения 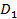, отличающиеся о стационарных значений D_01, соответствующих постоянным во времени электрическим полям. [1]

       Полагая, что отклонение 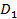 от стационарного значения  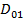не велико, можно написать следующее релаксационное уравнение:

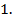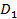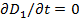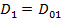       Уравнение ( 22) можно рассматривать как следствие фундаментальных положений термодинамики необратимых процессов. Если электрическое смещение  стационарно, то  и . Параметр  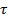представляет собой время диэлектрической релаксации.

       В случае периодических гармонических процессов уравнение ( 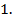23) принимает вид

       Отсюда следует, что:

       Из сопоставления (24) и (15) становится очевидным, что диэлектрическая проницаемость 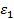 может быть представлена в комплексной форме:

       где 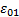 – «статическое» низкочастотное значение диэлектрической проницаемости.

       Реальные полимерные диэлектрики обычно описываются не одним временем релаксации, а спектром времен релаксации. Существует несколько причин, приводящих к появлению спектра времен релаксации. К их числу относятся: неодинаковая скорость протекания релаксационных процессов на различных участках тела и наличие различных релаксационных механизмов. [1] В случае полимеров к появлению спектров приводит уже само наличие длинных полимерных цепей и специфика межмолекулярного взаимодействия.

       В случае произвольного числа релаксационных процессов выражение ( 25) может быть представлено в виде:

       Таким образом, учитывая ( 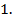26), и ( 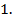20),(1,15), ( 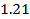), получаем:

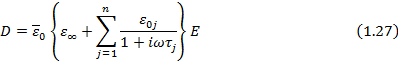
       Выражение, стоящее в скобках, можно рассматривать как оператор диэлектрической проницаемости:

       Этот оператор может быть представлен в дифференциальной форме:

       Сопоставляя выражения ( 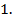17), ( 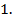18), ( 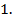20) и ( 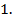27) и разделяя действительную и мнимую части в ( 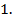26), получаем следующие выражения для  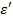и :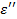

       Эти формулы указывают на наличие дискретного спектра времен диэлектрической релаксации, возникающего в полимере, находящемся в переменном электрическом поле. Переходя от дискретного спектра к сплошному, при 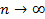 из уравнений ( 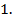30) и ( 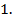31) получим:

       где 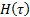 представляет собой плотность спектра времен диэлектрической релаксации.

       Рассмотрим случай 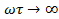. Тогд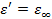а , а 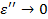. Для полимеров это условие соответствует или очень высоким частотам ( 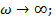. 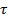=const ), или очень низким температурам( 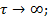. 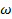=const). Значит, из феноменологической релаксационной теории следует, что при низких температурах можно ожидать уменьшения диэлектрической проницаемости  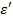и соответствующих потерь .

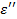       В другом предельном случае, когда 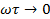, что соответствует низким частотам или сравнительно высоким температурам, 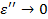, а 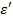 возрастает, достигая значения: