Исследовалась полимерная пленка ПИ Р-СОД толщиной ~ 2.8 мкм. Перед измерением каждая пленка покрыта с двух сторон фольгой, что обеспечивало равномерный электрический контакт по всей поверхности пленки. Пленка помещена между двумя электродами. После этого проводились два последовательных цикла нагрева и охлаждения образца. Первый нагрев проведен для снятия термической предыстории пленки и исключения структурных переходов, второй – для измерения диэлектрических свойств. В течение процедуры прогрева в интервале частот от 0.05 Гц до 3 МГц измерена частотная зависимость мнимой части комплексной диэлектрической проницаемости (𝜀′′(𝜔)), Рис. 3.9.
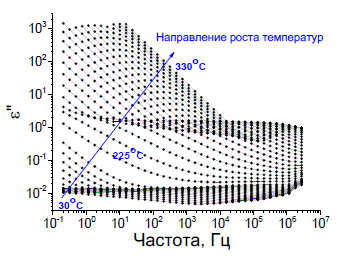
Рисунок 3.9. Зависимость мнимой части комплексной диэлектрической проницаемости пленки ПИ Р- СОД от частоты при изменении температуры в диапазоне от 30○C до 330○C с шагом 10○C при низких и шагом 5○C при высоких температурах [7].
По полученным результатам выполнена аппроксимация частотных зависимостей 𝜀′′ с использованием функций Кольрауша-Вильямса-Ваттса и Гаврильяка-Негами (2.9). В результате рассчитаны параметры 𝛼 и 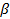 . Также был определен логарифм частоты, зависимость от обратной температуры которого представлена на Рис. 3.10 для обоих типов аппроксимации.
. Также был определен логарифм частоты, зависимость от обратной температуры которого представлена на Рис. 3.10 для обоих типов аппроксимации.
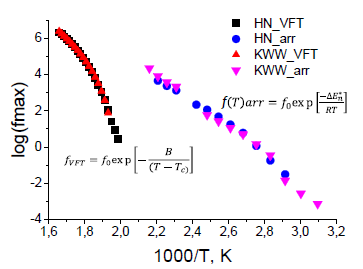
Рисунок 3.10 Зависимость логарифма частоты от обратной температуры для ПИ Р-СОД при использовании функции Кольрауша-Вильямса-Ваттса (KWW_VFT, KWW_arr) и Гаврильяка- Негами (HN_VFT, HV_arr) для аппроксимации частотных зависимостей диэлектрической проницаемости, представленных на Рис. 3.9 [7].
На Рис. 3.10 хорошо видно наличие двух релаксационных процессов: неаррениусовского 𝛼 -процесса (при температурах выше Tg) и аррениусовского 𝛽-процесса (при температурах ниже Tg) как для метода Гаврильяка-Негами, так и для метода Кольрауша-Вильямса-Ваттса. При высоких температурах зависимости частоты от обратной температуры практически совпадают. С понижением температуры различие между зависимостями логарифма частоты от обратной температуры начинает увеличиваться, но всё равно в рамках статических погрешностей результаты, полученные с помощью двух методов аппроксимации частотных зависимостей, отличаются слабо. Это свидетельствует о том, что в эксперименте оба метода могут использоваться для оценки энергий активации релаксационных процессов. C помощью аппроксимации температурных зависимостей уравнением Вогеля-Фолкера-Тамма определеяются значения энергий активаций для двух релаксационных процессов, 𝛼 и 𝛽, а также усредненные значения этих энергий активации по обоим используемым методам (Гаврильяка-Негами и Кольрауша-Вильямса-Ваттса). Полученные результаты представлены в Таблице 3.1.
Таблица 3.1. Значения энергии активации Ea для α- и β-релаксационных процессов, рассчитанные с помощью аппроксимации уравнениями температурных зависимостей времени релаксации, представленных на Рис. 3.10. [7]
| Рассчитываемые характеристики | α-релаксационный процесс | β-релаксационный процесс | ||
| Метод HN | Метод KWW | Метод HN | Метод KWW | |
| Ea, кДж/моль | 13.0 ± 1.0 | 8.3 ± 0.4 | 135.0 ± 5.0 | 151.0 ± 5.0 |
| <Ea>, кДж/моль | 11 ± 1 | 143 ± 5 | ||
Анализ полученных данных показывает, что значения энергии активации для α -релаксационного процесса на порядок меньше энергии активации для 𝛽-процесса. Стоит заметить, что напрямую сравнивать значения энергии активации двух релаксационных процессов 𝛼 и 𝛽 невозможно, потому что значение энергии активации Ea, отвечает за кооперативные перестройки полимерных цепей при температурах выше температуры стеклования. В отличие от энергии активации α-релаксационного процесса, энергия активация 𝛽-процесса характеризует локальную подвижность фрагментов повторяющихся звеньев в стеклообразном состоянии.
Заключение
Показано, что к основным показателям определяемым при диэлектрической спектроскопии относятся: диэлектрическая проницаемость, диэлектрические потери и тангенс угла диэлектрических потерь. На их величину основное влияние оказывает полярность молекул, которая, в свою очередь, определяется химическим составом полимерных молекул, частота внешнего электрического поля и температура, влияющая на время релаксации соответствующих форм тепловой подвижности.
Установлено, что у аморфных полимеров существует как минимум один высокотемпературный релаксационный переход 𝛼 и один низкотемпературный 𝛽, причем ширина пика у диэлектрического спектра у низкотемпературных процессов существенно больше. У аморфно-кристаллических полимеров зависимости существенно усложняются.
Выявлено, что существуют несколько методов проведения диэлектрической спектроскопии, но на диапазоне частот, интересном для материаловедения, наибольший интерес представляют мостовой метод и метод импедансного анализа. Для метода импедансного анализа наиболее оптимальным является диэлектрический спектрограф Novocontrol BDS Concept 80, который позволяет производить измерения в широкой частотной (от 3 мкГц до 3 ГГц) и температурной (-160 – 400 0С) областях. Для анализа диэлектрических спектров используется уравнение Гаврильяка–Негами, которое при использовании различных значений параметров α и β включает в себя модели частотной дисперсии Дебая, Коул-Коула и Девидсона-Коула.
Описана методика чтения диэлектрических спектров и выявлено, что расчет времен релаксации может осуществляться по уравнению Аррениуса и Вогеля-Фолкера-Тамма вблизи температуры стеклования.
Для полимера ОАБ-ДК1 обнаружены 𝛼 – релаксационный процесс при 170 0С, 𝛽 – релаксационный процесс при 1400С и -релаксационный процесс при 100 0С. При температуре 1000С обнаружена подвижность в боковой цепи. Температура 1400С соответствует начало подвижности в основной цепи. А при 1800С начинается подвижность подвижность хромофоров. Температура расстеклования ОАБ-ДК1 составила 1400С.
У полиимидной тонкой пленки толщиной 2,8 мкм выявлена температура стеклования Tg=1810С и два релаксационных перехода: неаррениусовского 𝛼 -процесса (при температурах выше Tg) и аррениусовского 𝛽-процесса (при температурах ниже Tg). При этом энергия активации 𝛼 – релаксационного процесса (11 ± 1 кДж/моль) на порядок ниже чем для 𝛽 – релаксационного процесса (143 ± 5 кДж/моль)
Список литературы
1. Ткаченко Т.П. «Диэлектрические свойства тонких полимерных пленок и их изменения в процессе сорбции воды.» Курсовая работа, МАИ (НИУ), 2018, 40 стр.
2. П.Г. Бабаевский «Электрические свойства полимеров» Курс лекций по дисциплине «Физика полимеров» 2018 г.
3. Малышкина И.А. «Основы метода диэлектрической спектроскопии.» Учебное пособие. - М.: Физический факультет МГУ, 2012. – 80 с.
4. «Оборудование ИХТИ КГТУ» http://www.kstu.ru/servlet/contentblob?id=29542
5. Коржов А.А. « Исследование молекулярной подвижности нелинейно-оптических полимеров» ВКРМ, Казань, 2016, 74 стр.
6. «Ресурсный центр Санкт-Петербургского государственного университета» http://www.dfm.spbu.ru/dielectric-spectrometer.html
7. Добровский А.Ю. «Изучение локальной ориентационной подвижности термопластичного полиимида Р-СОД» ВКРБ. СПбГУ, 2017, 40 стр.
8. Павлов А.С. «Влияние поляризации во фторсодержащихролимерных сегнетоэлектриках на характеристики молекулярной подвижности и структуры» Диссертация на соискание ученой степени кандидата химических наук, Москва, 2015, 158 стр.
9. Волков А.С., Копосов Г.Д., Перфильев Р.О.,. Тягунин «Анализ экспериментальных результатов по модели Гавриляка–Негами в диэлектрической спектроскопии» Оптика и спектроскопия, 2018, том 124, вып. 2, стр 206-209.
10. Jacobs, J.D. Dielectric characteristics of polyimide CP2 / J.D. Jacobs, M.J. Arlen, D. H. Wang, Z. Ounaies, R. Berry, L.S. Tan, P.H. Garrett, R.A. Vaia // Polymer – 2010. – V. 51. – № 14. – P. 3139–3146.
Дата: 2019-07-31, просмотров: 455.