В теории Дебая диэлектрическая релаксация в переменном электрическом поле
описываются следующим образом. Если к идеальному полярному диэлектрику прикладывать ступенчато возрастающую напряженность поля 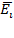 через заданные периоды времени ti до момента времени t, то в соответствии с принципом суперпозиции Больцмана происходит суммирование электрических смещений (поляризаций) в среде диэлектрика в соответствие с уравнением (1.14) и длительностью действия полей:
через заданные периоды времени ti до момента времени t, то в соответствии с принципом суперпозиции Больцмана происходит суммирование электрических смещений (поляризаций) в среде диэлектрика в соответствие с уравнением (1.14) и длительностью действия полей:
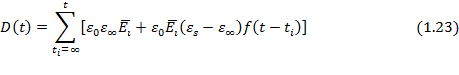
Если напряженность поля изменяется непрерывно во времени, то общее дифференциальное уравнение для электрического смещения в идеальном полярном диэлектрике имеет вид:
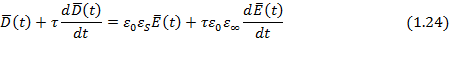
Если напряженность поля непрерывно изменяется по синусоидальному закону или в терминах комплексных чисел
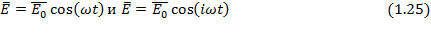
где: w - круговая частота, связанная с периодической частотой соотношением: 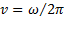 ;
; 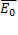 – амплитудное значение напряженности поля;
– амплитудное значение напряженности поля; 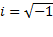
то в идеальном полярном диэлектрике возникает поляризация переменного направления, и ориентация диполей неизбежно отстает от прилагаемого поля. Математически это выражается как отставание по фазе на угол  электрического смещения:
электрического смещения:
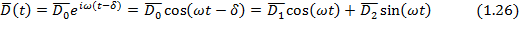
где 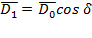 и
и 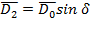 .
.
Отсюда определяется комплексная относительная диэлектрическая проницаемость 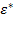 и две ее компоненты: действительная часть
и две ее компоненты: действительная часть 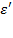 и мнимая часть
и мнимая часть 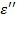 , или фактор потерь. Их отношение дает тангенс угла потерь.
, или фактор потерь. Их отношение дает тангенс угла потерь.
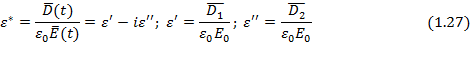

Решение общего дифференциального уравнения для электрического смещения в идеальном полярном диэлектрике (уравнение 1.24) для частного случая гармонических колебаний напряженности электрического поля с учетом действительных частей уравнений (1.25) и (1.26) дает так называемые уравнения диэлектрической дисперсии Дебая для частотных зависимостей комплексной относительной диэлектрической проницаемости 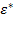 , ее компонент (
, ее компонент ( 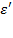 ,
, 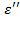 ) и тангенса угла потерь:
) и тангенса угла потерь:
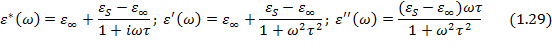
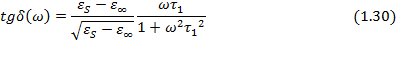
Время релаксации t 1 в уравнении (1.30) отличается от времени релаксации t, входящего в формулы (1.29) и связано с ним соотношением:

Вуравнениях диэлектрической дисперсии Дебая 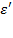 , соответствующая действительной части комплексной диэлектрической проницаемости, характеризует относительную диэлектрическую проницаемость диэлектрика при заданной частоте и общую накопленную энергию поляризации за период. Величины
, соответствующая действительной части комплексной диэлектрической проницаемости, характеризует относительную диэлектрическую проницаемость диэлектрика при заданной частоте и общую накопленную энергию поляризации за период. Величины 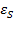 и
и 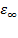 характеризуют наибольшее и наименьшее значения
характеризуют наибольшее и наименьшее значения 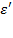 , определяемые способностью полимеров к статической поляризации: к общей дипольно-ориентационной и деформационной (при w®0) и только к деформационной поляризации (при w®∞) соответственно. Коэффициент, или фактор диэлектрических потерь
, определяемые способностью полимеров к статической поляризации: к общей дипольно-ориентационной и деформационной (при w®0) и только к деформационной поляризации (при w®∞) соответственно. Коэффициент, или фактор диэлектрических потерь 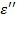 , соответствующий мнимой части комплексной диэлектрической проницаемости, характеризует рассеяние энергии электрического поля на молекулярное трение в процессе поляризации в виде тепла за период колебаний.
, соответствующий мнимой части комплексной диэлектрической проницаемости, характеризует рассеяние энергии электрического поля на молекулярное трение в процессе поляризации в виде тепла за период колебаний.
На рис. 3.6 схематически показаны зависимости ε ¢ , ε ² и tg d от частоты в различном выражении (lgw и произведение w t ) для дебаевской модели дипольной поляризации с одним временем релаксации.
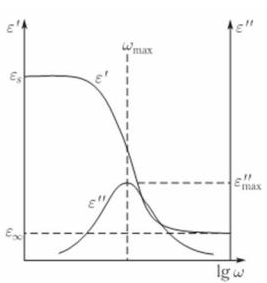
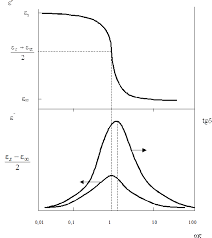
(а) (б)
Рисунок 1.1 Частотные зависимости показателей диэлектрических свойств идеального диэлектрика: (а) от логарифма частоты; (б) от произведения частоты на время релаксации [2].
Часто эти зависимости выражают через комплексную диэлектрическую восприимчивость 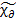 и ее действительную и мнимую составляющие (Рисунок 1.2 и уравнение 1.32)
и ее действительную и мнимую составляющие (Рисунок 1.2 и уравнение 1.32)
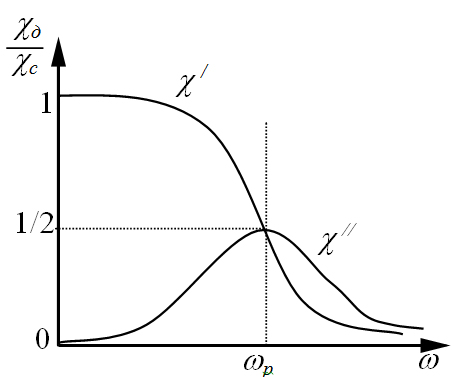
Рисунок 1.2 Частотные зависимости действительной и мнимой составляющей комплексной диэлектрической восприимчивости (χ=ε-1) [2].
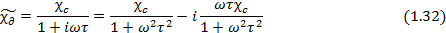
где 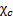 – статическое значение диэлектрической восприимчивости.
– статическое значение диэлектрической восприимчивости.
Как уже указывалось, область частот, в которой наблюдается наиболее резкое изменения диэлектрических свойств идеального диэлектрика, соответствует его дисперсии. В этой области при критической частоте ω max частотная зависимость e ¢ проходит через точку перегиба, а ε ² - через максимум при частоте, произведение которой на время релаксации равно единице (w t =1). Значения e ¢ в точке перегиба и максимума e ² при w t = 1 равны, соответственно (Рис. 1.2 б):
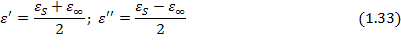
При этом максимальное значение tg d наблюдается при w t >1 и равно:

Уравнения (1.29-1.31) и кривые, приведенные на рис.1.1, описывают частотные зависимости диэлектрических свойств идеального диэлектрика при заданном времени дипольной релаксации, т.е. при заданной температуре. Изменение температуры приводит к изменению времени релаксации и, соответственно, формы кривых на рис.3.6. С другой стороны, если в уравнения (1.29-1.31) вставить время релаксации как функцию температуры в соответствие с уравнениями Аррениуса и ВЛФ (см. уравнения 1.21 и 1.22), то уравнения (1.29-1.31) будут описывать температурные зависимости диэлектрических свойств идеального диэлектрика при заданной частоте. В соответствие с этим процессы дипольной, также как и механической релаксации, подчиняются принципу температурно-временной или (в случае переменного электрического поля) температурно-частотной аналогии, т.е. повышение частоты аналогично понижению температуры.
На рис. 1.3 схематически показаны частотные (при двух различных температурах) и температурные (при двух различных частотах) зависимости e ¢ и e ² идеального полярного диэлектрика с одним типом дипольной релаксации.


Рисунок 1.3. Зависимости e¢ и e ² идеального полярного диэлектрика от частоты (а) при двух различных температурах (Т2 > Т1) и от температуры (б) при двух различных частотах ( w 2 > w 1) [2].
Пики показателя потерь e ² и области перегиба на кривых e ¢ при частотах w m 1 , w m 2 и температурах Т m 1 ,Т m 2 на этих зависимостях, соответствуют частотным (при заданной температуре) и температурным (при заданной частоте) релаксационным переходам для данного процесса дипольно-ориентационной поляризации. При этом время дипольной релаксации может быть рассчитано при наличии частотных зависимостей диэлектрических свойств для температур Т1 или Т2 (см.рис.1.3а) по частотам wm1 и wm1: 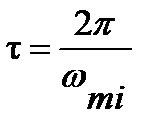 , а при наличии температурных зависимостей (см.рис.1.3б) для температур Т m 1 и Т m 2 по частотам w1 и w 2:
, а при наличии температурных зависимостей (см.рис.1.3б) для температур Т m 1 и Т m 2 по частотам w1 и w 2: 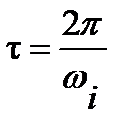 . При использовании уравнения Аррениуса для описания температурной зависимости времени дипольной релаксации (см. уравнение 1.21) по прямым в координатах
. При использовании уравнения Аррениуса для описания температурной зависимости времени дипольной релаксации (см. уравнение 1.21) по прямым в координатах 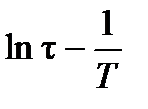 определяется энергия активации D E этого процесса. Все это служит основанием для использования температурных и/или частотных зависимостей диэлектрических свойств, так называемой диэлектрической спектроскопии, для исследования молекулярного теплового движения в полярных, в том числе полимерных, диэлектриках.
определяется энергия активации D E этого процесса. Все это служит основанием для использования температурных и/или частотных зависимостей диэлектрических свойств, так называемой диэлектрической спектроскопии, для исследования молекулярного теплового движения в полярных, в том числе полимерных, диэлектриках.
В твердом полимере обычно имеется несколько отчетливых релаксационных процессов, которые диэлектрически активны, если связаны со значительной ориентацией молекулярных диполей. Множественность релаксационных процессов отчетливо проявляется на температурной зависимости диэлектрических потерь, измеренных при фиксированной частоте (рис. 1.4). При повышении температуры постепенно активизируются различные типы молекулярной подвижности и связанных с ней диполей. Общепринято обозначать релаксационные процессы буквами α, β и т.д., начиная с высоких температур. Те же самые релаксационные процессы ответственны за дисперсию механических свойств, хотя те или иные процессы молекулярной перегруппировки могут сильнее проявляться в диэлектрических, чем в механических свойствах, и наоборот.
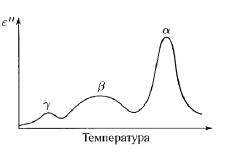
Рисунок. 1.4 Схематическая кривая температурной зависимости диэлектрических потерь [3].
Некоторые полимеры имеют полностью аморфную структуру, и в них присутствует только одна фаза. В этом случае всегда наблюдается высокотемпературный α-процесс, связанный с микроброуновским движением полимерных цепей, а также по крайней мере еще один низкотемпературный процесс (β, γ и т.д.). Относительная интенсивность α- и β-процессов определяется степенями ориентации дипольных групп, допускаемыми ограниченной подвижностью β- процесса и большей подвижностью α-процесса: каждый процесс молекулярной перестройки связан с определенным уровнем ориентации дипольных моментов.
Подробное исследование релаксационных процессов требует измерения диэлектрической проницаемости и потерь в изотермическом режиме в зависимости от частоты f, с тем, чтобы сравнить интенсивность молекулярной подвижности и энергии активации времен релаксации различных процессов. Типичный вид зависимостей e ² и e ² от lgf изображен на рис. 1.5. С помощью серии таких измерении можно получить зависимости времени релаксации индивидуальных процессов от температуры.
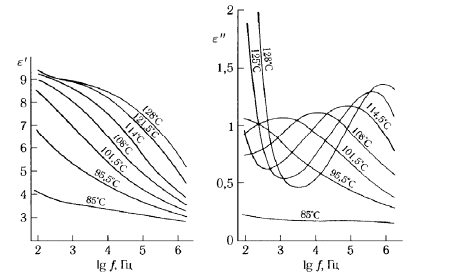
Рисунок. 1.5 Диэлектрические спектры поливинилхлорида в области α-процесса [3].
Локальные процессы (β-, γ- и др.)
Высокочастотные пики β-, γ- и т.д. в аморфных полимерах очень широкие: ширина на полувысоте достигает нескольких десятичных порядков (в сравнении с 1,14 порядка для дебаевского процесса), несмотря на линейную аррениусовскую зависимость времени релаксации от температуры, что указывает на некооперативный механизм релаксации. Для β-релаксации характерны сравнительно небольшие значения энергии активации (порядка 20-60 кДж/моль). Основные механизмы этого процесса:
1. Вращение боковой группы вокруг связи С-С. Этот механизм может быть связан с небольшой группой, например —CH2Cl, или с боковой цепью большего размера, например —СООС2Н5.
2. Конформационный переворот цикла. Типичный пример - циклогексильная группа. Переход из одной конформации кресла в другую изменяет ориентацию полярного заместителя
3. Локальные движения сегмента основной цепи. Ограниченные локальные движения в основной цепи встречаются часто, например, когда полярная группа соединена непосредственно с основной цепью полимера и не может двигаться независимо от нее. Такой же механизм характерен для случая последовательности четырех и более звеньев СН2 и объясняется вращением по типу коленчатого вала вокруг двух коллинеарных связей С-С. Наименьший фрагмент цепи (СН2)n, допускающий такое вращение независимо от остальной части цепи - это (СН2)4.
Кооперативные процессы (α-)
Пик α-релаксационного процесса для аморфного полимера обычно намного уже β-пика, хотя и существенно шире пика дебаевского процесса. Температурная зависимость α-процесса, как правило, также более сильная, что указывает на большую энергию активации, необходимую для крупномасштабных движений. Искривление температурной зависимости частоты релаксации для α-процесса показано на рис. 1.6а.
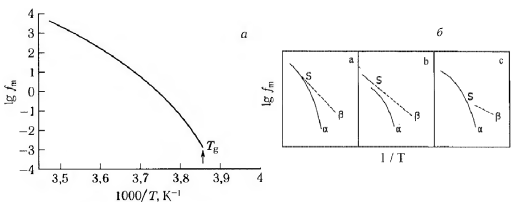
Рисунок. 1.6 Искривление аррениусовской зависимости частоты релаксации от температуры для α-процесса (а); три сценария разделения α- и β- процессов (б) [3].
В некоторых полимерах α-процесс благодаря большей энергии активации близок к β-процессу, в результате чего α- и β-пики сливаются (рис. 1.6б). Разделение пиков возможно, если проводить измерения при высоком давлении, когда α-процесс существенно подавляется из-за уменьшения свободного объема.
Молекулярная структура во многом определяет температуру стеклования и соответствующие времена диэлектрической релаксации. Так, объемные боковые группы могут уменьшать Tg, препятствуя плотной упаковке полимерных цепей, и наоборот.
Когда в полимере отсутствуют полярные группы, диэлектрическая релаксация может проявляться очень слабо, хотя процессы молекулярной перегруппировки имеют место. В этом случае можно искусственно усилить диэлектрические эффекты добавлением небольшого количества полярных групп, не влияющих заметным образом на другие свойства системы. Некоторые молекулярные процессы в неполярных полимерах могут случайно проявиться вследствие воздействия движения полимерных цепей на смещение небольших молекул примесей, среди которых могут быть полярные или ионные молекулы. Таким же образом малые концентрации полярных примесей могут резко увеличить диэлектрические потери неполярного полимера в определенном диапазоне частот.
В частично кристаллических полимерах, в которых сосуществуют кристаллическая и аморфная фазы, релаксационный спектр имеет более сложный вид. В дополнение к ориентационным процессам исключительно в аморфных областях имеются другие, присущие кристаллическим областям и межфазным границам.
Дата: 2019-07-31, просмотров: 422.