Большинство полимеров являются типичными диэлектриками. В полимерах, помещенных в электрическое поле, возникает электрический момент, т.е. происходит электрическая поляризация. Поляризация единицы объема диэлектрика, которую называют вектором поляризации, может быть представлена в виде формулы (1):

где 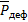 - поляризация, обусловленная деформацией электронных оболочек или смещением атомных ядер;
- поляризация, обусловленная деформацией электронных оболочек или смещением атомных ядер; 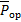 - поляризация, обусловленная ориентацией постоянных диполей.
- поляризация, обусловленная ориентацией постоянных диполей.
Постоянные диполи характеризуются величиной дипольного момента:

где q – заряд; l – расстояние между зарядами.
В отсутствие электрического поля постоянные диполи распределены хаотически; суммарный дипольный момент такой системы равен нулю. При наложении электрического поля происходит некоторая ориентация диполей, и возникает ориентационный электрический момент, характеризуемый вектором поляризации 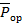 . Роль постоянных диполей в полимерах играют полярные группы. Например, в случае поливинилового спирта (ПВС) таким диполем является группа С-ОН[1].
. Роль постоянных диполей в полимерах играют полярные группы. Например, в случае поливинилового спирта (ПВС) таким диполем является группа С-ОН[1].
В неполярных диэлектриках при наложении электрического поля также возникает электрический момент 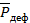 . В этом случае под действием электрического поля в молекулах диэлектрика происходит смещение электрических зарядов, и возникают наведенные электрические диполи. [1] Момент одного наведенного диполя p пропорционален напряженности приложенного электрического поля:
. В этом случае под действием электрического поля в молекулах диэлектрика происходит смещение электрических зарядов, и возникают наведенные электрические диполи. [1] Момент одного наведенного диполя p пропорционален напряженности приложенного электрического поля:

где 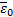 - электрическая постоянная (
- электрическая постоянная ( 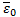 =8,85*10-12Ф/м);
=8,85*10-12Ф/м); 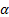 – некоторый коэффициент, который называется поляризуемостью молекул.
– некоторый коэффициент, который называется поляризуемостью молекул.
У диэлектриков любого типа (кроме сегнетоэлектриков) вектор поляризации связан с напряженностью поля простым соотношением:

Безразмерный параметр 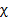 называется диэлектрической восприимчивостью диэлектрика. Иногда диэлектрической восприимчивостью называют произведение
называется диэлектрической восприимчивостью диэлектрика. Иногда диэлектрической восприимчивостью называют произведение 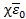 .
.
В ряде случаев диэлектрическая восприимчивость неполярных диэлектриков равна 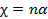 , где n – число наведенных диполей, содержащихся в единице объема, а
, где n – число наведенных диполей, содержащихся в единице объема, а 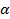 - поляризуемость молекулы. Соотношение
- поляризуемость молекулы. Соотношение 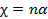 является приближенным. [1] Точное значение диэлектрической восприимчивости выводится в дальнейшем.
является приближенным. [1] Точное значение диэлектрической восприимчивости выводится в дальнейшем.
Электрические свойства диэлектриков характеризуются величиной электрического момента, возникающего при наложении на него электрического поля. Деформационная составляющая 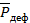 этого момента устанавливается очень быстро за время, равное 10-13 – 10-14 с. Время установления ориентационного момента в значительной степени зависит от температуры, от формы молекул, от сил взаимодействия между молекулами.
этого момента устанавливается очень быстро за время, равное 10-13 – 10-14 с. Время установления ориентационного момента в значительной степени зависит от температуры, от формы молекул, от сил взаимодействия между молекулами.
При рассмотрении электрических свойств диэлектриков важное значение имеет расчет напряженности электрического поля, действующего на атом или молекулу. [1] Напряженность такого локального поля равна:

где 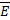 – напряженность макроскопического поля;
– напряженность макроскопического поля; 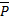 характеризует поле, обусловленное поляризацией всех других атомов или молекул материала.
характеризует поле, обусловленное поляризацией всех других атомов или молекул материала.
Важное значение при описании электрических свойств твердых диэлектриков имеет не только величина напряженности макроскопического поля 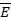 внутри диэлектрика, но и величина электрической индукции (электрического смещения)
внутри диэлектрика, но и величина электрической индукции (электрического смещения) 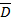 . В анизотропных твердых телах электрическая индукция является тензорном. Связь между величинами
. В анизотропных твердых телах электрическая индукция является тензорном. Связь между величинами 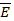 и
и 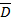 позволяет определить диэлектрическую проницаемость твердого тела.
позволяет определить диэлектрическую проницаемость твердого тела.
Для изотропной среды:
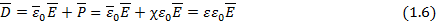
Отсюда диэлектрическая проницаемость:

где 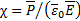 .
.
В соответствии с формулой ( 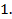 5) выражение (
5) выражение ( 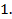 3) для индуцированного дипольного момента неполярной молекулы записывается следующим образом:
3) для индуцированного дипольного момента неполярной молекулы записывается следующим образом:

Тогда электрический момент единицы объема диэлектрика можно представить в виде:

Отсюда следует, что

Сравнивая соотношения ( 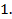 4) и (
4) и ( 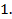 10), получаем:
10), получаем:

Очевидно, что при 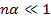 диэлектрическая восприимчивость
диэлектрическая восприимчивость 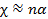 . Последнее соотношение справедливо для разреженных газов. Формулу (1.11) можно записать в виде:
. Последнее соотношение справедливо для разреженных газов. Формулу (1.11) можно записать в виде:

Учитывая, что 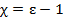 получаем соотношение Клазиуса - Мосотти, которое согласуется с результатами экспериментов [1] в случае кристаллов кубической системы, неполярных жидкостей и газов:
получаем соотношение Клазиуса - Мосотти, которое согласуется с результатами экспериментов [1] в случае кристаллов кубической системы, неполярных жидкостей и газов:

Ранее упоминалось, что при внесении диэлектрика в электрическое поле ориентация диполей происходит в течении некоторого времени. Если электрическое поле отключить, то из-за теплового движения спустя некоторое время 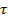 поляризация диэлектрика уменьшится в е раз. [1] Это явление получило название диэлектрической релаксации, а время
поляризация диэлектрика уменьшится в е раз. [1] Это явление получило название диэлектрической релаксации, а время 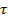 называется временем диэлектрической релаксации. Значит поляризуемость молекул диэлектрика
называется временем диэлектрической релаксации. Значит поляризуемость молекул диэлектрика 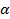 ( как и параметры
( как и параметры 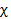 и
и 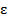 ), помещенного в периодически изменяющееся электрическое поле, должна зависеть от периода изменения этого поля
), помещенного в периодически изменяющееся электрическое поле, должна зависеть от периода изменения этого поля 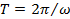 , времени релаксации
, времени релаксации 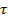 и соотношения между
и соотношения между 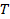 и
и 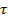 .
.
1.2 Релаксационная теория дипольно-ориентационной поляризации Дебая.
Деформационная (электронная) поляризация молекулярных, в том числе полимерных, диэлектриков в электрическом поле обусловлена практически мгновенным обратимым деформированием электронных облаков (характерные частоты их колебаний относительно ядер атомов обычно превышают 1012 Гц) и соответствует малой величине предельной диэлектрической проницаемости 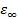 , равной квадрату коэффициента преломления:
, равной квадрату коэффициента преломления:

Поскольку деформационная поляризация непосредственно не связана с активационным тепловым движением, то она является нерелаксационным, практически мгновенным процессом, формально аналогичным мгновенно-упругой деформации в процессах механической релаксации вязко-упругих тел. В противоположность деформационной дипольно-ориентационная поляризация и обратный ей процесс деполяризации обусловлены протеканием сравнительно медленных обратимых процессов установления равновесной ориентации постоянных диполей (полярных молекул, групп или звеньев) вдоль поля, т.е. постепенным установлением их средней ориентации на фоне тепловых колебаний. Таким образом, дипольно-ориентационная поляризация является типичным релаксационным процессом возврата системы в равновесное состояние после вывода из него приложением электрического поля.
В настоящее время отсутствует достаточно строгая обобщенная теория диэлектрической релаксации полимеров, поэтому к ним применяется фундаментальная теория, впервые разработанная Дебаем применительно к диэлектрической релаксации в идеальных диэлектриках - молекулярных полярных жидкостях. Эта теория базируется на двух основных положениях:
· на экспоненциальном характере установления равновесной ориентации диполей - больцмановском распределении ориентаций диполей под действием внешнего электрического поля на фоне тепловых колебаний;
· на принципе суперпозиции – при линейной зависимости поляризации от напряженности приложенного поля дополнительное поле даст пропорциональное увеличение электрического смещения.
Релаксационная теория дипольной поляризации Дебая базируется на феноменологическом подходе. Если к идеальному полярному диэлектрику, не имеющему остаточной поляризации, не содержащему свободных носителей зарядов (ионов и электронов) и дипольная поляризация которого является линейной функцией напряженности поля, мгновенно приложить электрическое поле напряженностью 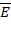 , то общее электрическое смещение D ( t ), равное поляризация Р( t ) в любой момент времени t описывается суммой двух членов:
, то общее электрическое смещение D ( t ), равное поляризация Р( t ) в любой момент времени t описывается суммой двух членов:
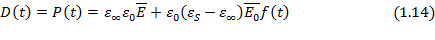
Первый член этого уравнения соответствует мгновенному отклику диэлектрика на приложенное поле, т.е. не зависящей от времени деформационной поляризации 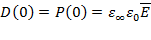 , а второй – кинетике достижения предельного значения дипольной поляризации
, а второй – кинетике достижения предельного значения дипольной поляризации 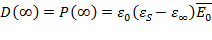 , описываемой кинетической функцией
, описываемой кинетической функцией 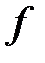 (t):
(t):

При этом 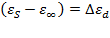 - предельный вклад дипольно-ориентационной поляризации в относительную диэлектрическую проницаемость, где
- предельный вклад дипольно-ориентационной поляризации в относительную диэлектрическую проницаемость, где 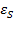 - статическая диэлектрическая проницаемость полярного диэлектрика,
- статическая диэлектрическая проницаемость полярного диэлектрика, 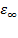 - диэлектрическая проницаемость, обусловленная деформационной поляризацией.
- диэлектрическая проницаемость, обусловленная деформационной поляризацией.
Для определения кинетической функции дипольной поляризации используется постулат неравновесной термодинамики, в соответствие с которым для линейного процесса релаксации его скорость пропорциональна движущей силе процесса, т.е. степени отклонения системы от равновесия. Движущей силой процесса дипольно-ориентационной поляризации, протекающей во времени, является разность 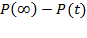 , где
, где 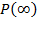 - предельная (равновесная) поляризация. Следовательно, скорость дипольно-ориентационной поляризации должна быть пропорциональна этой разности:
- предельная (равновесная) поляризация. Следовательно, скорость дипольно-ориентационной поляризации должна быть пропорциональна этой разности:

где:  – коэффициент пропорциональности, или константа скорости релаксационного процесса, обратная величина которой
– коэффициент пропорциональности, или константа скорости релаксационного процесса, обратная величина которой 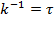 является характерной временной константой процесса и называется временем диэлектрической релаксации. Интегрирование уравнения (1.16) по времени дает уравнение кинетики дипольно-ориентационной поляризации:
является характерной временной константой процесса и называется временем диэлектрической релаксации. Интегрирование уравнения (1.16) по времени дает уравнение кинетики дипольно-ориентационной поляризации:
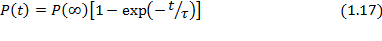
Из сравнения этого уравнения с уравнением (1.15) следует, что кинетическая функция дипольно-ориентационной поляризации имеет вид:

При 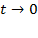
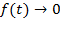 и
и 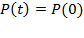 , а при
, а при 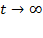
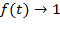 и
и 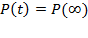 .
.
При 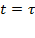 функция
функция 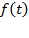 претерпевает перегиб и в этой области изменяется наиболее резко, т.е. кинетическая область перехода от
претерпевает перегиб и в этой области изменяется наиболее резко, т.е. кинетическая область перехода от 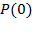 к
к 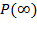 . характеризует область наиболее резкого изменения поляризации, и, соответственно, изменения диэлектрической проницаемости от
. характеризует область наиболее резкого изменения поляризации, и, соответственно, изменения диэлектрической проницаемости от 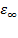 к
к 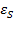 , называемая областью дисперсии диэлектрической проницаемости. При этом величина
, называемая областью дисперсии диэлектрической проницаемости. При этом величина 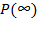 характеризует накопление в диэлектрике, помещенном между пластинами конденсатора, максимального результирующего заряда Qmax, а производная
характеризует накопление в диэлектрике, помещенном между пластинами конденсатора, максимального результирующего заряда Qmax, а производная 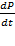 соответствует поляризационному (емкостному или зарядному) току, который при достижении
соответствует поляризационному (емкостному или зарядному) току, который при достижении 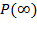 имеет максимальное значение.
имеет максимальное значение.
При мгновенном отключении электрического поля кинетическая функция спада поляризации (деполяризации) для идеального полярного диэлектрика имеет вид:

а кинетика его дипольной деполяризации описывается уравнением:

Возникающий в процессе деполяризации разрядный ток будет изменяться по этому же закону.
Характерная временная константа (время релаксации) дипольной поляризации и деполяризации  равно времени, в течение которого предельная ориентационная поляризация после отключения тока уменьшается в e раз. Величина
равно времени, в течение которого предельная ориентационная поляризация после отключения тока уменьшается в e раз. Величина  для конкретного релаксационного процесса, протекающего в идеальном полярном диэлектрике зависит только от температуры. Эта зависимость описывается уравнением Аррениуса (для полимеров – при температуре выше температуры стеклования Tg):
для конкретного релаксационного процесса, протекающего в идеальном полярном диэлектрике зависит только от температуры. Эта зависимость описывается уравнением Аррениуса (для полимеров – при температуре выше температуры стеклования Tg):

где: 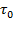 – предэкспоненциальный множитель,
– предэкспоненциальный множитель, 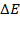 – энергия активации процесса дипольной поляризации,
– энергия активации процесса дипольной поляризации,  – газовая постоянная,
– газовая постоянная,  – абсолютная температура, или уравнением ВЛФ (вблизи области стеклования):
– абсолютная температура, или уравнением ВЛФ (вблизи области стеклования):
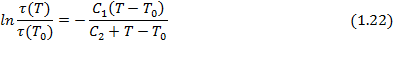
где: 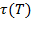 ,
, 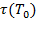 - время релаксации при заданной температуре Т и при стандартной температуре (температуре приведения)
- время релаксации при заданной температуре Т и при стандартной температуре (температуре приведения) 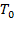 соответственно; С1, С2 – константы, зависящие от выбора Т0 (если Т0=Т g, то С1=17,44; С2=54,4 К; t(Т g)=1013c).
соответственно; С1, С2 – константы, зависящие от выбора Т0 (если Т0=Т g, то С1=17,44; С2=54,4 К; t(Т g)=1013c).
Поскольку электрическое смещение (поляризация) в среде диэлектрика при заданной напряженности поля в любой момент времени связана с показателями диэлектрических свойств - диэлектрической проницаемостью и восприимчивостью (см. уравнениe (1.6), то кинетика изменения этих свойств во времени после мгновенного включения или отключения статического электрического поля описывается этими же уравнениями (1.14 - 1.21), а их температурные зависимости определяются температурными зависимостями времени релаксации (уравнения 1.21-1.22).
Дата: 2019-07-31, просмотров: 376.