Сконструировать нелинейный регулятор, используя начальную неупрощенную модель бака.
Расчетное соотношение для регулятора –
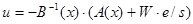
e=z – x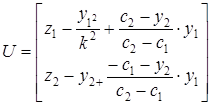 
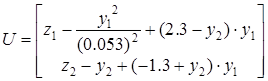
Конструирование программного регулятора
Используя линеаризованную модель в дискретном времени, записать программу перевода системы из состояния 
в состояние
; 
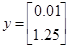
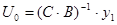
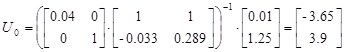
Анализ свойств сконструированной системы с оптимальным П регулятором
Построить процесс в системе с П. регулятором
Для построения процесса графика необходимо пользоваться следующую формулу
В итоге получаются следующие графики переходных процессов. Для сравнения приведены переходные процессы для систем без компенсаторов (штрихованная линия)
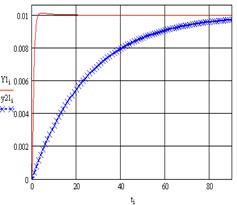
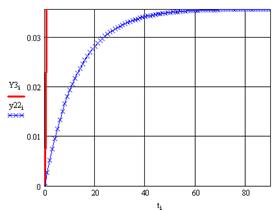
Рисунок 17 – Сопоставление качеств переходного процесса первого и второго выхода с компенсатором и без него.
Из графика видно, что система выходит на установившееся значение раньше если на ней стоит компенсатор.
Вычислить критерий оптимальности в системе
Величина критерия с удельным регулятором вычисляется
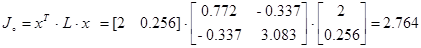
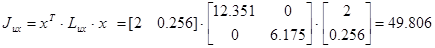
Отклонение параметров на 10 процентов
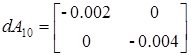
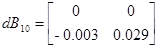
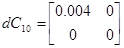
Отклонение параметров на 5 процентов
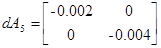
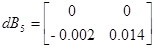
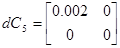
Матрицы чувствительности будут рассчитаны в пункте 3.4:
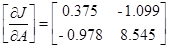
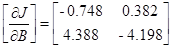
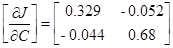
В конечном счете, получаем
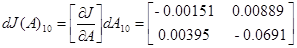
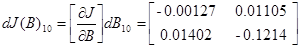
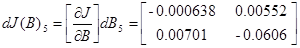
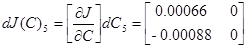
Оценить потерю качества от децентрализации
Коэффициент передачи децентрализованного регулятора найден в пункте 2.5
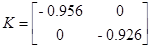
Для определения критерия
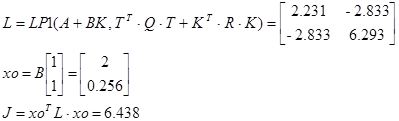
Вычислить чувствительность системы
dJ/dA, dJ/dВ, dJ/dС, dJ/dК для системы (А1,В, С), где А1=А+В*К, К=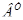 
*Р.
Матрицы А1 и P (решение уравнения Риккати) Pлп (решение уравнения Ляпунова ) рассчитывались ранее
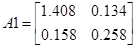
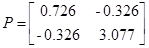
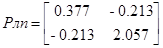
Для расчета матрицы V следует решить уравнение Ляпунова вида:
А1*V+V* А1+I=0
Таким образом :
; 
;
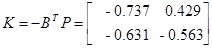Все необходимые составляющие для расчета чувствительности у нас есть:
dJ/dA=2∙P∙V==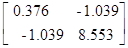 
;
dJ/dВ=2∙P∙V∙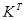 
= 
;
dJ/dС=2∙ ∙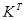 
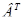∙P∙V+2∙ 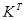∙K∙V=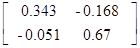 
;
dJ/dК =2∙K∙V+2∙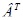 
∙P∙V=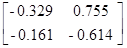 
Анализ робастности системы с надежным регулятором
Матрицы отклонения начальной системы
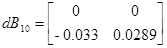
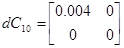
То есть аа=0.00 8 1; bb =0.0 289 ; cc =0.00 4 .
Подставляя значения, полученные в пункте 2.6
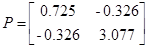
в уравнение Scherzinger найдем из нее новую матрицу
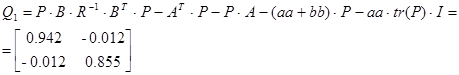
Т.к. определенная матрица положительно определенная
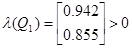
то сконструированная система робастная поэтом стационарная и при изменении параметров в расчетных диапазонах величина критерия изменяется очень мало.
Решение обратной задачи конструирования
Записав расцеплояющей регулятор в виде
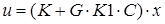
Далее используя соотношение
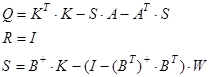
где W – произвольная матрица выбирается из условия S >0
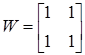
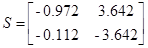
В конечном счете, получаем
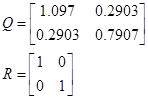
Дата: 2019-07-30, просмотров: 218.
