Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

       

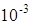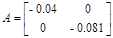
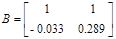
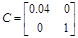
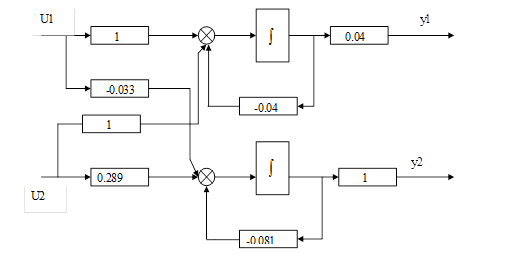
Рисунок 1. – Структурная схема в исходной форме

        

 

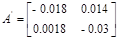
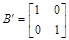
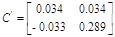
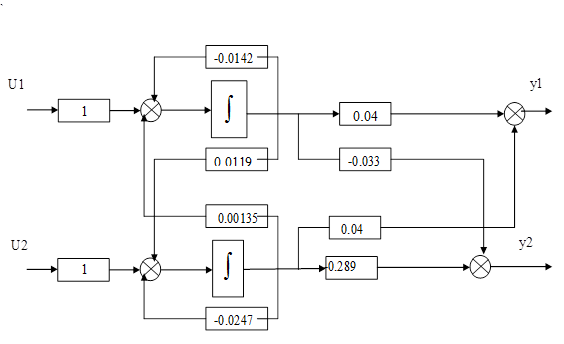
Рисунок 2. – Структурная схема в форме Ассео

 

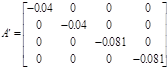
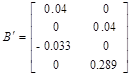
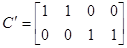
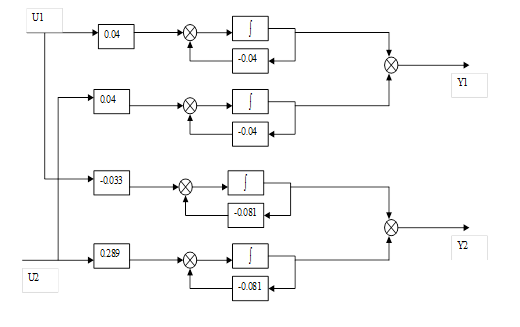
Рисунок 3. – Структурная схема в форме ВСП

Линеаризованная модель в непрерывном и дискретном времени с датчиками и ИМ

 

a)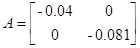

 

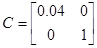
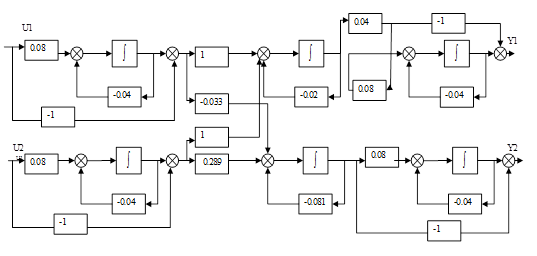
Рисунок 4. – Структурная схема системы в непрерывном времени

 

 

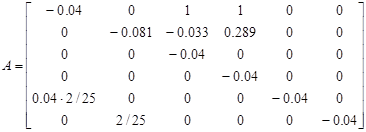
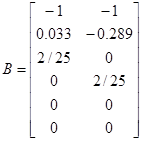
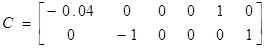
б) в дискретном времени

 

Рисунок 5. – Структурная схема системы в дискретном времени

 

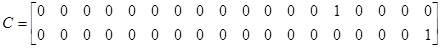
Модель с генератором возмущений

Соединив последовательно модель шумов с моделью системы, в общем случае запишем новою модель системы в виде

w 1= w 2=100; g 1= g 2=0.02

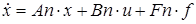
где 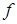 - белый шум

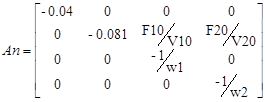
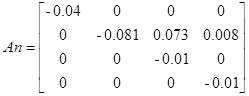
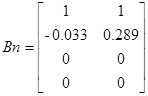
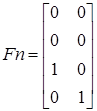
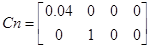
Условие правомерности децентрализации

Система в форме Ассео:

 

                 

 

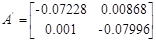
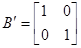
Для децентрализованной системы

 

 

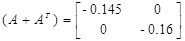
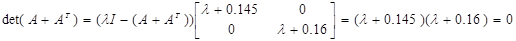
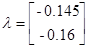
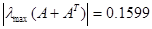
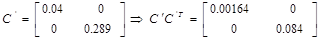
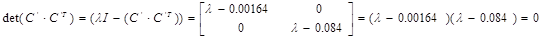
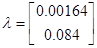
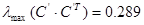
Спектральная норма матрицы С’, то есть максимальное сингулярное число матрицы:

 

 

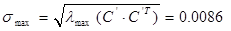
Спектральная норма матрицы F:

 

 

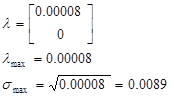
Погрешность составляет:

 

 

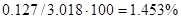
Можно предположить, что децентрализация является допустимой. Децентрализованная модель запишется в виде:

 

                 

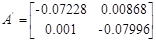
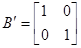
Анализ качественных свойств системы

а)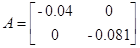  

 

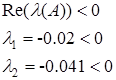
Следовательно, матрица является гурвицевой.

 

б)

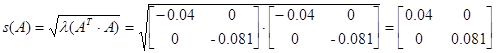
max s1(A)=||A||2= 0.081<1

 

Следовательно, матрица А является нильпотентной.

Проверить, является ли система (А, В, С) постоянной, управляемой, наблюдаемой, идентифицируемой с вектор - столбцом х = (1; 1.25), параметрически инвариантной, минимальнофазовой, расцепимой, астатической.

а) постоянство:

 

 

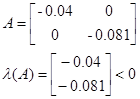
Следовательно, система является постоянной.

 

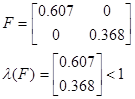
Следовательно система является постоянной.

б) управляемость:

 

 ;

 

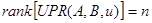
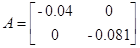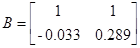
По первому входу:

 

 

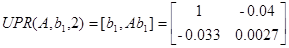
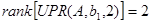
Система управляема по первому входу.

По второму входу:

 

 

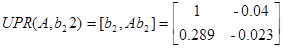
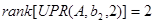
Система управляема по второму входу.

в) наблюдаемость:

 

   

 

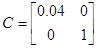
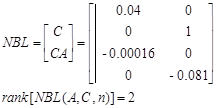
Система наблюдаема.

г) идентифицированость

 

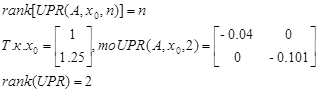
Система идентифицируема.

д) параметрическая инвариантность:

 

    

 

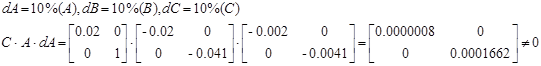
Система не инвариантна относительно отклонения dA.

 

 

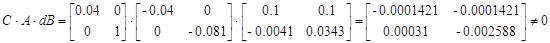
Система не инвариантна относительно отклонения dB.

 

 

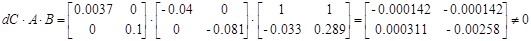
Система не инвариантна относительно отклонения dС.

е) минимальнофазовость и астатичность:

 

 

 

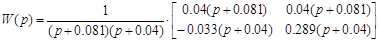
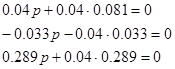
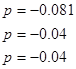
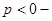система является минимальнофазовой и астатической.

ж) расщепление:

 .

 

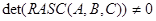
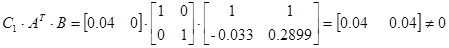
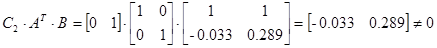
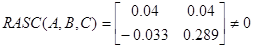Исследование процессов в системе и анализ количественных свойств системы

Построение графиков кривой разгона непрерывной системы

Построение графика решения у(t) для системы {А, В, С}, есл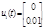и  и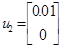

 

 

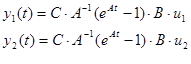
Таблица 5 Значение выходов непрерывной системы

Возмущение	Реакция выхода системы y(t)
u1=0 u2=0,01	Y1 Y2 10-3	0	3.874	6.247	7.701	8.591	9.137	9.471	9.676	9.802	9.878
		0	-2.548	-3.523	-3.896	-4.038	-4.093	-4.114	-4.122	-4.125	-4.126
u1=0,01 u2=0	Y1 Y2	0	3.874	6.247	7.701	8.591	9.137	9.471	9.676	9.802	9.878
		0	0.023	0.03	0.034	0.035	0.035	0.036	0.036	0.036	0.036
время t, с		0	12	24	37	49	61	74	86	98	111

 

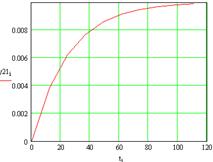
Рисунок 6 – Реакция первого выхода на возмущения u1(t)       

 

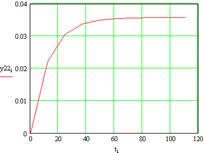
Рисунок 7 – Реакция второго выхода на возмущения u1(t)

 

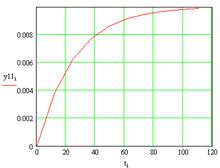
Рисунок 8 – Реакция первого выхода на возмущения u2(t)

 

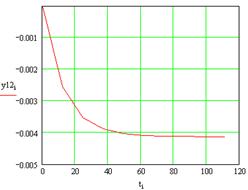
Рисунок 9 – Реакция второго выхода на возмущения u2(t)