Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Введение

 

Проблема модернизации системы управления смесительного бака с целью улучшения его техника – экономических показателей требует решения следующих задач.

Исследование свойств технологического агрегата как многомерной системы для чего необходимо провести эквивалентное и аппроксимационое преобразование модели; провести анализ качественных и количественных свойств системы; идентифицировать многомерную математическую модель по данным эксперимента.

Конструирование многомерных регуляторов для рассматриваемого смесительного бака:

П. – регулятор, апериодический регулятор, децентрализованный регулятор, надежный регулятор, блочно – иерархический регулятор, регулятор для билинейной и для нелинейной модели, программный регулятор.

Оценка качества в замкнутой автоматической системы регулирования и выбор наилучшего типа регулятора.

Исследование свойств технологического агрегата как многомерной системы

Многомерная математическая модель агрегата

Нелинейная модель агрегата

Вывод нелинейной модели агрегата. На примере рассмотрим конкретную техническую систему – смесительный бак:

 

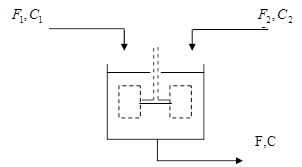
Рисунок 1. Модель бака

 

F₁,F₂,F - потери жидкости на истоке и притоке системы, м³/с;

C₁,C₂,C - концентрация на истоке и притоке системы, Кмоль/м³;

h - уровень жидкости в баке, м;

S - площадь бака,м²;

V - объем жидкости в баке,м³;

Запишем уравнение системы в стационарном (установленном) состоянии, когда приток равняется истоку (уравнение материального баланса):

 

F₁₀+F₂₀-F₀=0 ; C₁ ,

 

где индекс 0 означает установившееся состояние.

 Записавши условия баланса кинетической и потенциальной энергии на выходе из бака (имеется в виду, что жидкость вытекает самостоятельно)

 

,

 

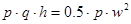где

p - плотность жидкости, кг/м³;

w - скорость истока, м/с;

q - ускорение свободного падения,q=9.81 м/с²;

и допуская, что

d - диаметр выходного трубопровода, м.

Получим:

 

,

 ,

 

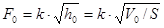где

k – коэффициент.

При изменении потерь в системе происходит накоплении вещества и переход до нового установленного состояния. Этот переходный процесс описывается дифференциальными уравнениями

 

 

 

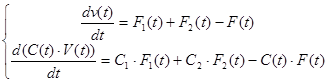
Где dv/dt – приращение объема жидкости, 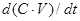- прирост массы жидкости.

Приведем эту систему в стандартном состоянии:

Обозначим:

 

 

 

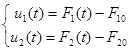
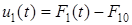 – изменение во времени отклонения потери от номинального по отношению к первому каналу.

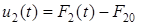– изменение во времени отклонения потери от номинального по отношению ко второму каналу.

 

 

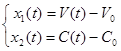
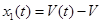 – изменение во времени отклонения объема от номинального в баке;

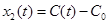 – отклонение концентрации от номинального значения;

 

 

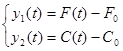
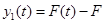 – изменение потерь на выходе;

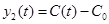 – изменение концентрации на выходе.

 

Запись билинейной модели

Уравнение билинейной системы записывается в виде

 

 

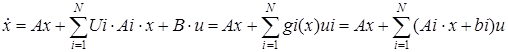
Приняв допущение, что критерий оптимальности в форме О.А. Красовского

 

 

регулятор определяется по зависимости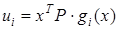

Где матрица определена как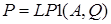

Линеаризованная модель

Линеаризуем зависимость 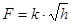, разложив ее на ряд Тейлора.

 

 

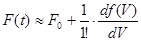
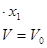
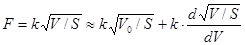
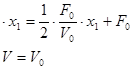
С учетом ранее изложенного запишем:

 

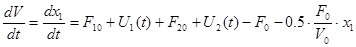
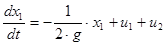; (т.к. 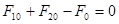), где ;

 

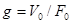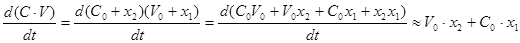
Припустив в случае остатка 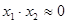. Тогда, подставив производную 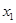, получим

 

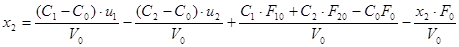
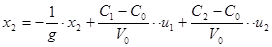
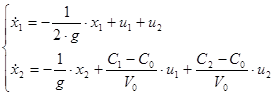
Представим систему в матричной форме:

 

 

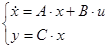
Тогда матрицы А и В запишутся в виде

 

,

 

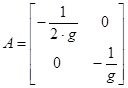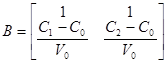
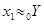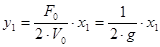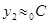
Для определения матрицы С необходимо установить связь между векторами x и y. Т.к. , , то

 

; , то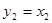

 

Тогда

 

 

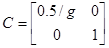
Система будет иметь вид

 

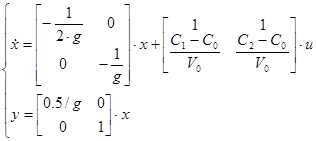
Коэффициенты модели системы:

 

            

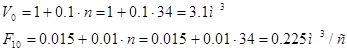
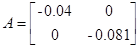
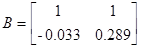
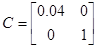
Модель в дискретном времени

Система в дискретном времени имеет вид:

 

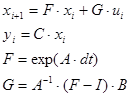
dt= 24 c.

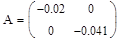
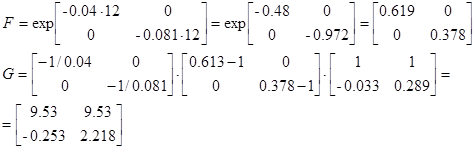
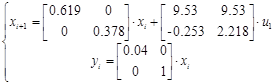
Зададим 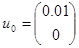, , 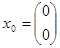получим значения на выходах дискретной системы.

 

Таблица 4 Значение выходов дискретной системы

Возмущение	Реакция выхода системы y(t)
u1=0.01 u2=0	y1 y2	0 0	0.00384 -0.00254	0.00624 -0.00352	0.0077 -0.03896	0.00859 -0.004038	0.00913 -0.00409	0.00947 -0.00411
время t, с		0	12	24	37	49	61	74

1.1.7 Преобразование модели в форме Ассео

 

 

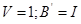
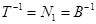
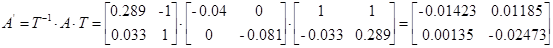
Внешне связное форму получаем из матрицы передаточных функций

 

 

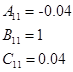
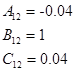
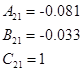
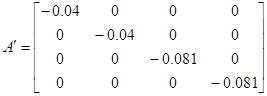
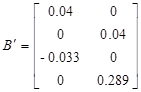
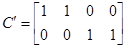
Вычисление МПФ системы

 

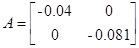
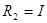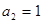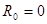; ;  ; n=2; i=1;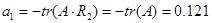

 

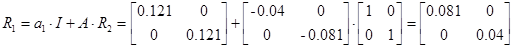
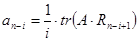
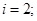
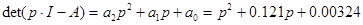
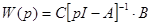
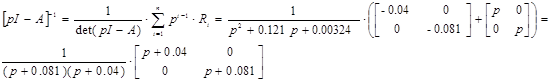
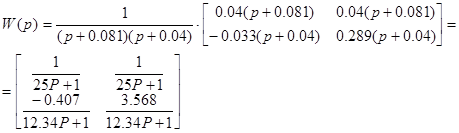
Активная идентификация

Для дискретной формы системы ( F , G , C ) из пункта 3. 1. провести реализацию системы.

Запишем систему в виде:

 

 

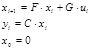
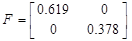
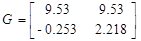
Подавая импульс по первому входу, рассчитаем:

 

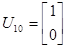
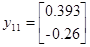
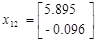
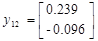
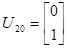
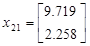
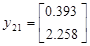
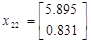
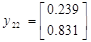
Теперь имея экспериментальные данные, сгруппировав их в матрицы H и H ₁ можем приступить к их обработки.

 

 

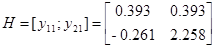
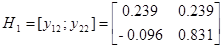
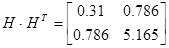
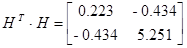
Из собственных векторов от ( 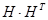) и ( 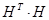) построим:

 

 

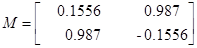
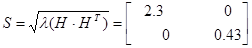
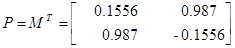
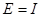
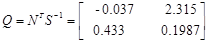
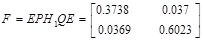
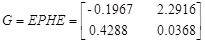
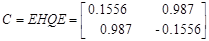
Для проверки идентификации найдем коэффициент передачи системы

 

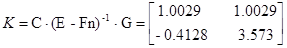
Коэффициент передачи, вычисленный по исходным матрицам

 

 

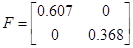
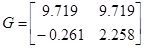
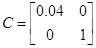
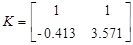
Можно сделать вывод о том, что система идентифицирована, верно

 

Пассивная идентификация

Для дискретной формы системы (F, G, C) из пункта 3. 1. провести пассивную идентификацию системы, предполагая, что вектор входа изменяется соответственно таблице:

 

Таблица 7 Значение вектора входа для пассивной идентификации.

Такт, n	0	1	2	3	4	5
U(n)	0.01	0	0	0.04	0	0
	0	0.01	0.02	0	0.03	0

 

 

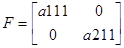
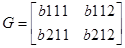
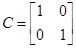
Используя матрицы системы в дискретной форме для заданных значений вектора входа, рассчитаем значения вектора выхода

 

 

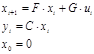
Результаты расчета сведем в таблицу:

Такт, n	1	2	3	4	5	6
y(n)	0.003935	0.006321	0.012	0.023	0.026	0.016
	-0.0026	0.022	0.053	0.0091	0.071	0.026

Используя данные эксперимента (Таблица 8) можем приступить непосредственно к определению параметров идентифицированной системы

Тогда

 

 

 

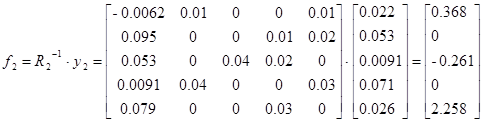
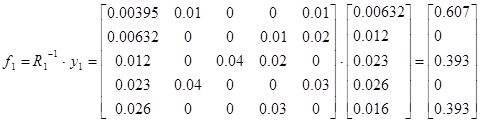
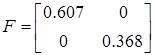
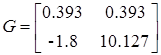
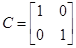
Для проверки идентификации найдем коэффициент передачи системы

 

 

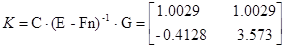
Система идентифицирована, верно

В ыводы

 

Исследован технический объект – смесительный бак. Получен спектр модели: линейная, нелинейная, экспериментальная и аналитическая модель. Проведены эквивалентное аппроксимационое преобразование модели агрегата

Исследованы качественные и количественные свойства системы. Разработаны регуляторы управления объектом: П. – регулятор;

апериодический регулятор; надежный регулятор; блочно – иерархический регулятор; регулятор для билинейной и для нелинейной модели; программный регулятор; регулятор с компенсатором взаимосвязей. А также компенсаторы возмущений и компенсаторы на задании.

Проанализированы процессы в сконструированной системе с регулятором в качественном и количественном отношении (построен процесс в системе с регулятором, вычислен критерий оптимальности, проанализирована робастность, решена обратная задачи конструирования ).

На основании данного анализа можно сделать вывод о том, что наиболее подходящим регулятором для рассмотренной системы является оптимальный П. – регулятор. Хотя он и обладает некоторым перерегулированием, имеет небольшую статическую ошибку (при отсутствии компенсатора на задание), однако все эти недостатки компенсируются его простотой в установке и обслуживании. Помимо этого он обладает наименьшим временем переходного процесса, неплохим показателем критерия оптимальности. В силу своей простоты он является более надежным в том плане, что вероятность выхода из строя самого регулятора мала.

Литература

1. Стопакевич А.А., Методические указания к практическим занятиям по курсу « Основы системного анализа и теория систем » для бакалавров по автоматики. – Одесса: ОНПУ, 1997.

2. Стопакевич А.А. Сложные системы: анализ, синтез, управление. – Одесса: ОНПУ 2004

Введение

 

Проблема модернизации системы управления смесительного бака с целью улучшения его техника – экономических показателей требует решения следующих задач.

Исследование свойств технологического агрегата как многомерной системы для чего необходимо провести эквивалентное и аппроксимационое преобразование модели; провести анализ качественных и количественных свойств системы; идентифицировать многомерную математическую модель по данным эксперимента.

Конструирование многомерных регуляторов для рассматриваемого смесительного бака:

П. – регулятор, апериодический регулятор, децентрализованный регулятор, надежный регулятор, блочно – иерархический регулятор, регулятор для билинейной и для нелинейной модели, программный регулятор.

Оценка качества в замкнутой автоматической системы регулирования и выбор наилучшего типа регулятора.

Исследование свойств технологического агрегата как многомерной системы