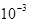Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Система в дискретном времени имеет вид:

 

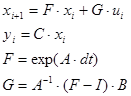
dt=24 c.

   

 

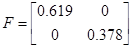
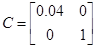
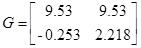
Зададим , , 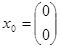получим значения на выходах дискретной системы, которые совпадают с расчетом задания в п.4.

 

Таблица 6 Значение выходов дискретной системы

Возмущение	Реакция выхода системы y(t)
u1=0.01   u2=0	y1 y2 10-3	0	0	3.874	6.247	7.701	8.591	9.137	9.471	9.676	9.802	9.878
		0	0	-2.548	-3.523	-3.896	-4.038	-4.093	-4.114	-4.122	-4.125	-4.126
такт		0	1	2	3	4	5	6	7	8	9	10

 

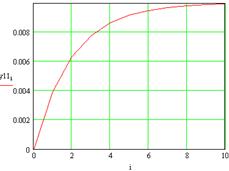
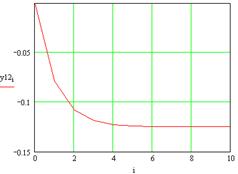
Рисунок 10 – Реакция выходов системы на возмущения u (t)

Построение графиков кривой разгона нелинейной системы

Данные для построения графиков получены в пункте 1.1.2

Для первого выхода пользуемся таблицей 1. Получившиеся графики можем сопоставить с графиками полученным в пункте 1.3.1, введя поправку на начальное значение параметра

 

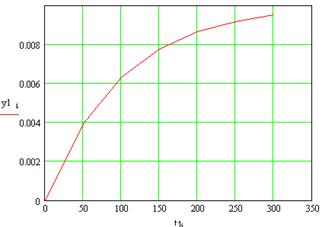
Рисунок 11 – Реакция первого выхода на  возмущения u1(t) в пункте 1.3.1

 

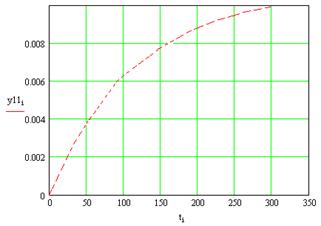
Рисунок 12 – Реакция первого выхода на возмущение для линеаризованной системы

 

Легко видеть, что эти график совпадают, что говорит о том, что линеаризация по первому выходу проведена на приемлемом уровне

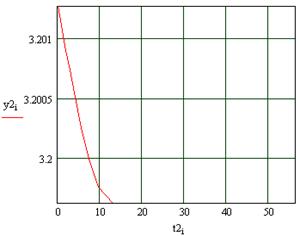
Рисунок 14 – Реакция второго выхода на возмущения u1(t) полученного в пункте 1.3.1

 

Рисунок 13 – Реакция второго выхода на  возмущения для линеаризованной системы

 

В данном случае имеет место погрешность которую можно связать с ошибкой вносимой кусочно – линейной аппроксимации.

 

Установившиеся состояния системы

Вычислить постоянное значение состояния системы в условиях

 

  

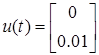
Т.к. установившееся значение предполагает отсутствие динамики, то систему можно записать в следующем виде

 

 

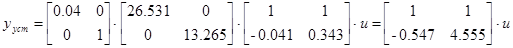
Идентификация многомерной математической модели по данным эксперимента

Активная идентификация

Для дискретной формы системы ( F , G , C ) из пункта 3. 1. провести реализацию системы.

Запишем систему в виде:

 

 

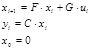
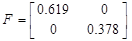
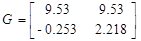
Подавая импульс по первому входу, рассчитаем:

 

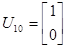
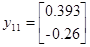
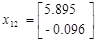
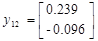
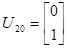
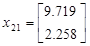
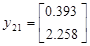
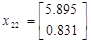
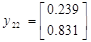
Теперь имея экспериментальные данные, сгруппировав их в матрицы H и H ₁ можем приступить к их обработки.

 

 

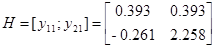
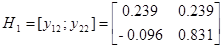
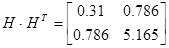
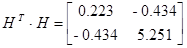
Из собственных векторов от ( 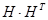) и ( 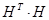) построим:

 

 

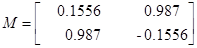
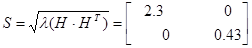
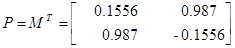
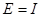
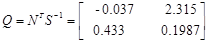
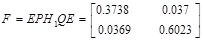
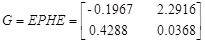
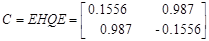
Для проверки идентификации найдем коэффициент передачи системы

 

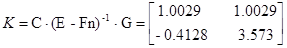
Коэффициент передачи, вычисленный по исходным матрицам

 

 

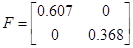
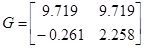
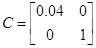
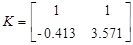
Можно сделать вывод о том, что система идентифицирована, верно

 

Пассивная идентификация

Для дискретной формы системы (F, G, C) из пункта 3. 1. провести пассивную идентификацию системы, предполагая, что вектор входа изменяется соответственно таблице:

 

Таблица 7 Значение вектора входа для пассивной идентификации.

Такт, n	0	1	2	3	4	5
U(n)	0.01	0	0	0.04	0	0
	0	0.01	0.02	0	0.03	0

 

 

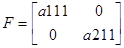
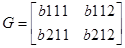
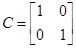
Используя матрицы системы в дискретной форме для заданных значений вектора входа, рассчитаем значения вектора выхода

 

 

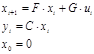
Результаты расчета сведем в таблицу:

Такт, n	1	2	3	4	5	6
y(n)	0.003935	0.006321	0.012	0.023	0.026	0.016
	-0.0026	0.022	0.053	0.0091	0.071	0.026

Используя данные эксперимента (Таблица 8) можем приступить непосредственно к определению параметров идентифицированной системы

Тогда

 

 

 

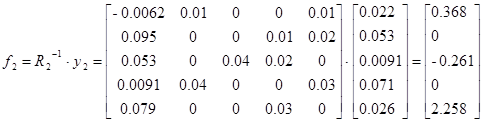
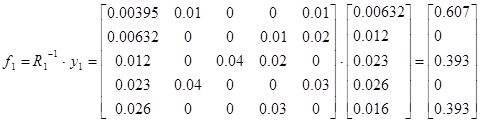
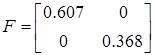
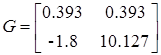
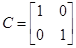
Для проверки идентификации найдем коэффициент передачи системы

 

 

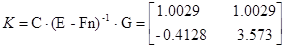
Система идентифицирована, верно