Конструирование П. - регулятора, оптимизирующего систему по интегральному квадратичному критерию
Регулятор состояния, который оптимизирует систему по критерию:
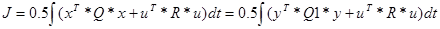
Определяется по соотношениям:
P=LR1(A,B,Q,R);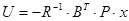 
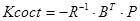При этом Q=R=I
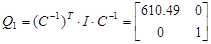
Т.к. матрица С. является инвертированной, для образования регулятора выхода нет необходимости конструировать наблюдатель состояния – недосягаемое состояние просто вычисляется по формуле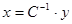 
.
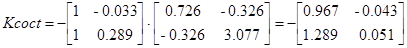
Следовательно, регулятор выхода имеет вид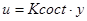 
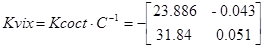
Конструирование компенсаторов заданий и измеряемых возмущений
Обозначивши через z заданное значение выхода y и припуская, что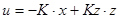 
, получим
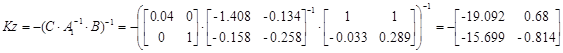
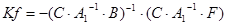
Приняв во внимание, что А=В
Если при компенсации возмущений и заданий учесть «стоимость» управления, записавши критерий в виде
,
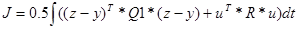то компенсаторы (оптимальные) определяются зависимостями
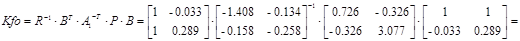
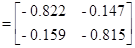
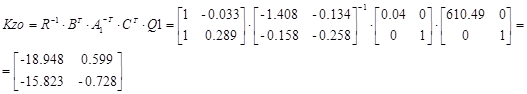
Значение выхода при действии возмущения f в системе без компенсаторов при z=0
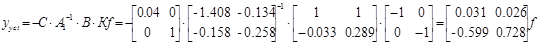
а также с оптимальным компенсатором.
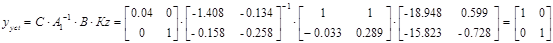
Конструирование регулятора с компенсатором взаимосвязей
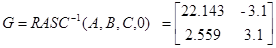
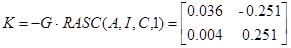
Проверим, или регулятор действительно расцепляет систему, т.е. матрица передаточных функций является диагональной
Используя V как новый вход можно далее записать
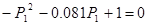
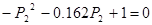
Регулятор выхода можно записать в виде
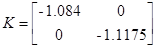
Конструирование апериодического регулятора
Апериодический регулятор для дискретной системы может быть получен: из условия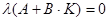 
. Запишем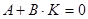 
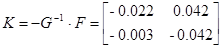
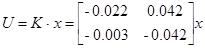
Конструирование децентрализованного регулятора
Используя форму Ассео, запишем:
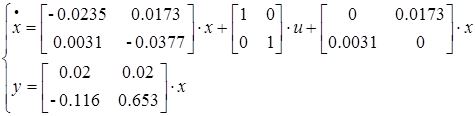
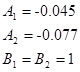
Следовательно, получим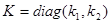 
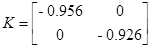
Для определения критерия
Конструирование надежного регулятора
Если матрица G моделирует отказы каналов измерения, то регулятор находится в виде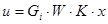 
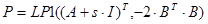
Берем s=0.04 При этом значении выполняются необходимые условия:
s>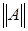 
Результат решения уравнения Ляпунова первого типа
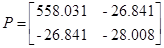
Коэффициент передачи надежного регулятора
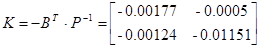
Поверим систему с регулятором на устойчивость
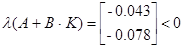
Следовательно, система является постоянной при любых отклонениях.
Конструирование блочно-иерархического регулятора
Воспользуемся регулятором состояния и проверим или можно создать последовательность регуляторов состояния.
; 
; 
; 
; 
|
|
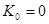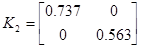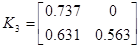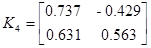
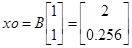
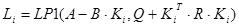
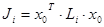
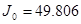
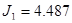
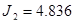
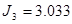
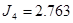
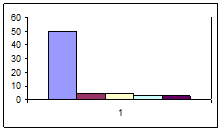
Рисунок 15 – Иллюстрация монотонного уменьшения величины критерия
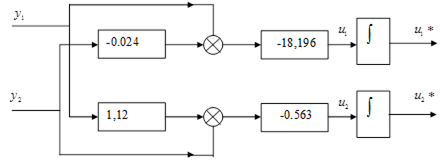
Рисунок 16 – Схема блочно – иерархического регулятора
Конструирование регулятора для билинейной модели
Билинейный регулятор определяется по следующей зависимости
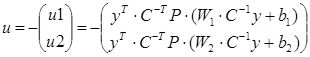
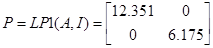
Вводя все компоненты в уравнение, получаем:
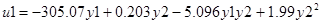
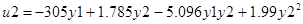
Дата: 2019-07-30, просмотров: 199.
