ПРЕДПРИЯТИЯ НА ОСНОВЕ МЕТОДА
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Цель занятия: закрепление знаний по теме «Финансовые результаты: формирование цены, прибыль и рентабельность», разработка ассортиментной политики предприятия.
Оборудование и программное оснащение
практического занятия.
Используемое оборудование - персональные ЭВМ типа IBM PC с соответствующими периферийными устройствами: дисплеем символьным, накопителем на магнитных дисках, и программа Microsoft Excel.
Методические указания.
При разработке методов анализа экономических процессов, относящихся к полностью определенным задачам, достаточно часто используются оптимизационные модели различного вида. Объектом исследования при этом являются только те ситуации, в которых имеется проблема поиска наилучшего по некоторым критериям (оптимального) варианта, значение показателя эффективности (целевой функции) которого является экстремальным при существующих ограничениях.
Общая задача математического программирования имеет вид
Определить экстремум функции
f(x) ® extremum (max, min)
при выполнении условий
gi(x) = (³, £)bi, (i = 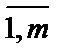 ),
),
x = (x1, x2,… xj …xn), xj ³ 0, (j = 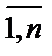 ),
),
где f(x) – целевая функция;
gi(x) – функция ограничения;
bi – действительное число, константа ограничения.
Если функции f(x) и gi(x) представлены в виде линейных функций, то оптимизационная задача называется задачей линейного программирования.
Постановка задачи.
Предприятие выпускает 4 вида продукции: П1, П2, П3, П4. Для ее изготовления используется 3 вида ресурсов: р1, р2, р3, объем которых ограничен. Известны потребность в ресурсах для каждого вида продукции, а также прибыль, получаемая от ее реализации.
Требуется определить оптимальное количество выпуска каждого вида продукции, при котором будет получена максимальная прибыль для предприятия.
Исходные данные данного примера представлены в табл. 3.5.1.
Таблица 3.5.1
| Показатель | Вид продукции | Тип ограничений | Значение ограничений | |||
| П1 | П2 | П3 | П4 | |||
| Единичная прибыль | 60 | 70 | 120 | 130 | ||
| Ресурс р1 сырье (тонн) | 1 | 1 | 1 | 1 | <= | 16 |
| Ресурс р2 оборудование (штук) | 4 | 6 | 10 | 13 | <= | 100 |
| Ресурс р3 трудовые ресурсы (человек) | 6 | 5 | 4 | 3 | <= | 110 |
| Нижняя граница | 1 | 2 | 2 | 1 |
| |
| Верхняя граница | 4 | - | - | 1 | ||
Обозначим через n1 – количество изделий вида П1, которое должна выпустить фирма;
n2 – количество изделий вида П2;
n3 – количество изделий вида П3;
n4 – количество изделий вида П4.
Прибыль от реализации четырех видов продукции должна быть максимальна:
f(n) = 60 × n1 + 70 × n2 + 120 × n3 + 130 × n4 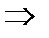 max
max
Однако накладывается ряд условий (на объемы производства каждого вида продукции и объемы используемых ресурсов).
n1 <= 4
n1 >= 1
n2 >= 2
n3 >= 2
n4 = 1
1 × n1 + 1 × n2 + 1 × n3 + 1 × n4 <= 16
4 × n1 + 6 × n2 + 10 × n3 + 13 × n4 <= 100
6 × n1 + 5 × n2 + 4 × n3 + 3 × n4 <= 110
Алгоритм решения задачи:
1. Ввести в таблицу исходные данные:
- начальные значения искомых переменных (П1-П4) разместить в ячейках В6:Е6;
- значения единичной прибыли – в ячейках В7:Е7;
- нормы расходов ресурсов (р1-р3) на каждый вид продукции поместить соответственно в ячейки В10:В12 – для П1, С10:С12 – для П2, D 10:D12 – для П3, E10:E12 – для П3.
- в ячейку G 6 поместить целевую функцию B7×B6+C7×C6+D7×D6+E7×E6;
- тип ограничений помещается в ячейки F 10: F 12, значения ограничений – в ячейки G 10: G 12;
- задать формулы для подсчета объема потребления каждого вида ресурса:
в ячейке Н10 для р1: B 10× B 6+ C 10× C 6+ D 10× D 6+ E 10× E 6;
в ячейке Н11 для р1: B 11× B 6+ C 11× C 6+ D 11× D 6+ E 11× E 6;
в ячейке Н12 для р1: B 12× B 6+ C 12× C 6+ D 12× D 6+ E 12× E 6;
- граничные условия задаются в ячейках: В14:Е14 – значения нижних границ, В15:Е15 – значения верхних границ.
Исходные данные представлены на рис. 3.5.1.
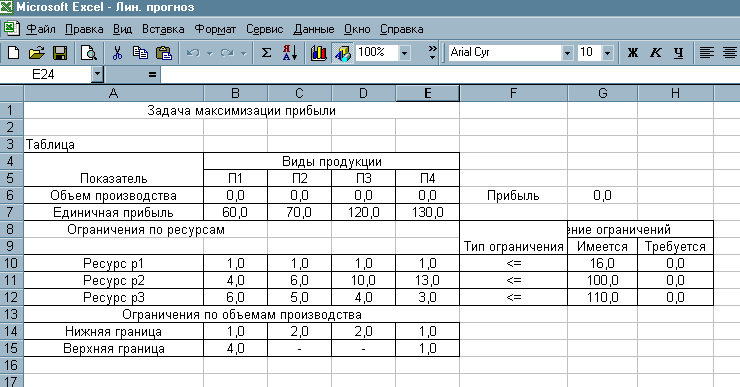
Рис. 3.5.1 – Таблица описания математической модели задачи
2. Открыть диалоговое окно Поиск решения (рис. 3.5.2) и ввести необходимые значения целевой функции, изменяемые решения, ограничения. В поле Параметры выбрать Линейную модель, нажать ОК и Выполнить.
Примечание: если в меню Сервис отсутствует команда Поиск решения, то необходимо выбрать в меню Сервис команду Надстройки, установить флажок рядом с именем Поиск решения.
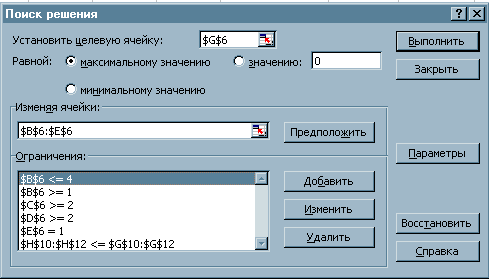
Рис. 3.5.2 – Диалоговое окно «Поиск решения» для задачи
максимизации прибыли.
Таким образом, получаем результат: программа определила значения объемов производства для каждого вида продукции и соответствующее значение целевой функции, выражающее получаемую при этом прибыль (таблица решения на рис. 3.5.3).
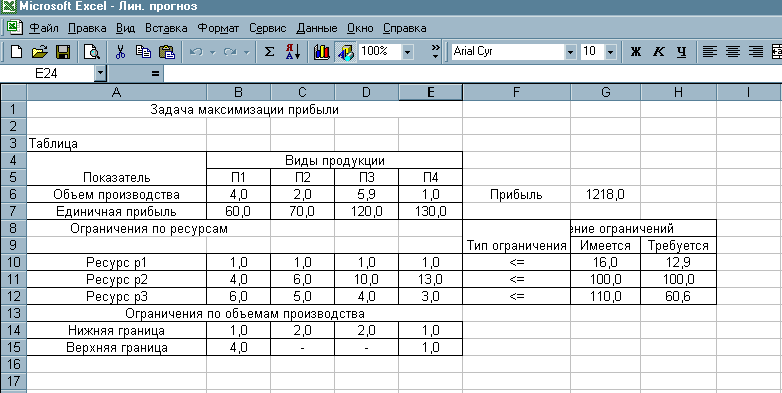
Рис. 3.5.3 – Результаты решения задачи.
Содержание и порядок выполнения практического занятия.
Студенту необходимо:
1. Ознакомиться с методическими указаниями и решить пример на основе представленного алгоритма.
2. Получить у преподавателя вариант заданий. Исходные данные по вариантам представлены в табл. 3.5.2.
Таблица 3.5.2
Показатели
Ограничения для ресурсов
Варианты
3. Решить задачу в соответствии со своим вариантом, сделать выводы на основе полученных данных.
4. В оперативном управлении особенно важно принимать верные решения в ситуациях отклонения ресурсов от первоначально запланированных.
а) Проанализировать, что произойдет с величиной прибыли предприятия, если отвлечь рабочих предприятия с одних работ на другие. Результаты представить в табл. 3.5.3.
Таблица 3.5.3
Изменение трудовых ресурсов
| План выпуска продукции | Условия | |||
| Перевести 10 рабочих | Перевести 30 рабочих | Перевести 50 рабочих | Перевести 60 рабочих | |
| П1 | ||||
| П2 | ||||
| П3 | ||||
| П4 | ||||
| Значение функции цели | ||||
б) Проанализировать, что произойдет планом производства при изменении количества оборудования.
Результаты представить в табл. 3.5.4.
Таблица 3.5.4
Изменение количества оборудования на предприятии
| План выпуска продукции | Условия | |||
| Сократить количество оборудования на 5 единиц | Сократить количество оборудования на 10 единиц | Увеличить количество оборудования на 10 единиц | Увеличить количество оборудования на 20 единиц | |
| П1 | ||||
| П2 | ||||
| П3 | ||||
| П4 | ||||
| Значение функции цели | ||||
На основе полученных значений функции целей в табл. 3.5.3 – 3.5.4 сделать вывод о недостаточном или излишнем количестве ресурсов.
5) проанализировать, как повлияет на результаты решения задачи, если отменить условия на ограничения объема производства для каждого вида продукции. То есть в диалоговом окне Поиск решения необходимо удалить ограничения на объемы производства, однако в поле Параметры необходимо установить флажок в поле Неотрицательные значения.
Дата: 2019-07-30, просмотров: 315.