Цель работы: Изучить законы стационарного движения жидкости.
Задача: Проверить опытным путем уравнение Бернулли, вычислив
экспериментально и теоретически расход жидкости.
Краткая теория
Раздел физики, в котором рассматривают законы равновесия и движения жидких и газообразных тел, а также их взаимодействия с твердыми телами, называют гидроаэромеханикой.
Характерное свойство жидких и газообразных тел – их текучесть, т.е. малая сопротивляемость деформации сдвига: если скорость сдвига стремится к нулю, то силы сопротивления жидкости или газа этой деформации также стремятся к нулю. Иными словами, жидкие и газообразные тела не обладают упругостью формы – они легко принимают форму того сосуда, в котором находятся. Вследствие этого внешнее давление, производимое на жидкость или газ, передается ими во все стороны равномерно (закон Паскаля).
Движение жидкостей или газов называют течением, а совокупность частиц движущейся жидкости или газа называют потоком. В гидромеханике отвлекаются от молекулярного строения жидкостей и газов, рассматривая их как сплошную среду.
Течение жидкости называют установившимся или стационарным, если скорость жидкости в каждой точке пространства, занятого жидкостью, не изменяется с течением времени, т.е. V не зависит от t. В случае неустановившегося течения V зависит также от времени t.
Течение называют ламинарным или слоистым в том случае, если поток представляет собой совокупность слоев, перемещающихся друг относительно друга без перемешивания. Течение называют турбулентным, если имеет место перемешивание различных слоев жидкости или газа вследствие образующихся завихрений.
В целях наглядности движение жидкости можно изображать с помощью линий тока, которые проводят так, что касательные к ним совпадают по направлению с векторами скоростей жидкости в соответствующих точках пространства. В случае стационарного течения линии тока не изменяются с течением времени и совпадают с траекториями отдельных частиц жидкости.
Поверхность, которая образована линиями тока, проведенными через все точки малого замкнутого контура, называют трубкой тока. Часть жидкости, ограниченную трубкой тока, называют струей.
В реальных жидкостях течение усложняется тем, что между отдельными слоями потока происходит внутреннее трение. Однако в ряде случаев влияние внутреннего трения невелико и им можно пренебречь. Жидкость, в которой отсутствует внутреннее трение, называют идеальной жидкостью. Поэтому изучая движение идеальной жидкости, можно установить ряд закономерностей, которые с известным приближением применимы к течению реальных жидкостей.
При переходе потока жидкости из трубки с большим диаметром Д  в трубку с меньшим диаметром Д
в трубку с меньшим диаметром Д 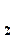 происходит увеличение скорости течения от значения V
происходит увеличение скорости течения от значения V  до значения V
до значения V 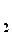 . Соотношение между скоростями течения V
. Соотношение между скоростями течения V  и V
и V 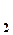 задается уравнением неразрывности струи: S V = Const
задается уравнением неразрывности струи: S V = Const
или для двух сечений: S  V
V  =S
=S 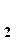 V
V 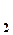 (1)
(1)
Если S = 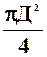 , то уравнение (1) перепишется: V
, то уравнение (1) перепишется: V  Д
Д 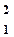 = V
= V 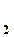 Д
Д  (2)
(2)
Изменение скорости течения влечет изменение давления, которое можно определить из уравнения Бернулли:

Для горизонтальной трубки уравнение Бернулли запишется:
 , отсюда
, отсюда
P  - P
- P 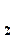 =
= 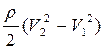 , (3)
, (3)
Где P  , V
, V  и P
и P 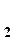 , V
, V 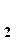 - давления и скорости в сечениях Д
- давления и скорости в сечениях Д  и Д
и Д  соответственно;
соответственно; 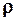 - плотность жидкости.
- плотность жидкости.
Решая совместно уравнения (2) и (3), найдем скорость течения V  :
:
V  =
= 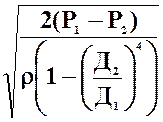 (4)
(4)
Воспользовавшись уравнением неразрывности струи, найдем секундный объемный расход жидкости:
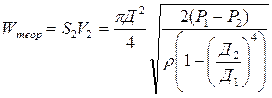 (5)
(5)
Экспериментально секундный объемный расход жидкости можно определить, измеряя время t наполнения жидкостью баллона объемом V:
W  =
=  (6)
(6) 
Сравнение результатов измерений секундного объемного расходов жидкости, полученным по формулам (5) и (6), может служить проверкой справедливости уравнения Бернулли.
Описание установки
На деревянной подставке закреплена стеклянная трубка переменного сечения. Диаметры узкой и широкой части трубки указаны на табличке возле установки.
Резиновая трубка соединяет прибор с водопроводным краном, а другая служит для слива воды.
Разность давлений, создаваемая струей жидкости, имеющей скорость V  в широкой части и скорость V
в широкой части и скорость V 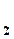 в узкой части, измеряется при помощи ртутного или водяного манометра. Трубка должна иметь горизонтальное положение.
в узкой части, измеряется при помощи ртутного или водяного манометра. Трубка должна иметь горизонтальное положение.
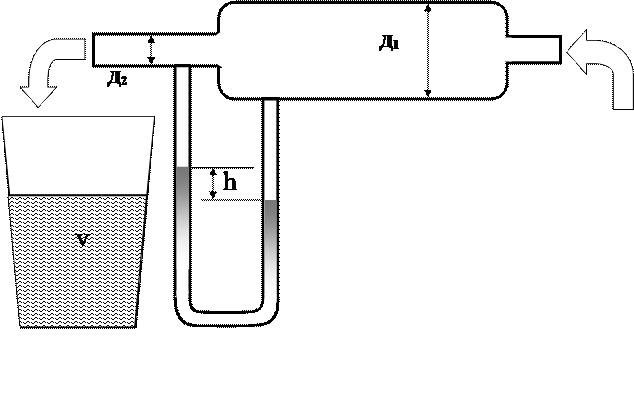 |
Рисунок 1- Схема установки с ртутным манометром
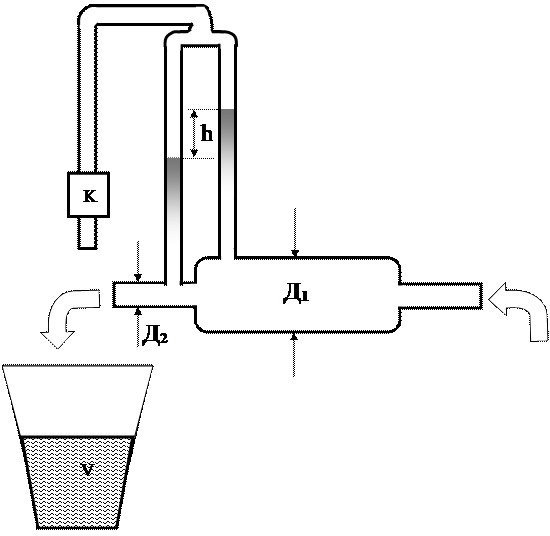 |
Рисунок 2- Схема установки с водяным манометром
Порядок выполнения работы
1. Через прибор пропускается вода из водопровода и измеряется разность уровней h в коленах манометра.
В формуле (5) разность давлений (P  - P
- P 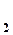 ) заменим по формулам:
) заменим по формулам:
P  - P
- P 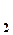 = (
= ( 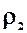 -
- 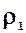 ) gh (для ртутного манометра)
) gh (для ртутного манометра)
и
P  - P
- P 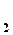 =
= 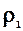 gh (для водяного манометра)
gh (для водяного манометра)
и получим формулы для расчета теоретического значения расхода жидкости:
- в установке с ртутным манометром:
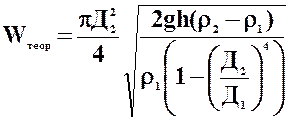 или так как Д
или так как Д  >> Д
>> Д  и
и 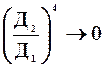
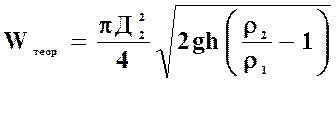
- в установке с водяным манометром:
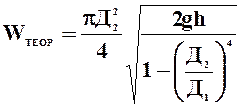
2. При помощи секундомера измерить время, в течение которого наполняется водой сосуд объемом V.
3. Рассчитать экспериментальный расход воды по формуле (6):

4. Измерения провести для разных значений h.
5. Результаты измерений и вычислений занести в таблицу результатов измерений и расчетов.
Таблица 1. Результаты измерений и расчетов
| № опыта | V | h | t | W 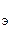
| Д 
| Д 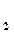
| W 
| 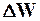
|
Контрольные вопросы
1. Дать определение идеальной жидкости.
2. Записать и сформулировать теорему неразрывности струи.
3. Записать и сформулировать уравнение Бернулли.
4. Как Вы в работе проверяли справедливость уравнения Бернулли?
Литература [1,4,7 ]
ЛАБОРАТОРНАЯ РАБОТА № 5
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ЖИДКОСТИ
Приборы и принадлежности:
1. трубка с оттянутым концом (бюретка);
2. технические весы с разновесами;
3. микроскоп “Мир - 1”;
4. сосуд с исследуемой жидкостью;
5. штатив.
Цель работы: определить коэффициент поверхностного натяжения воды.
Дата: 2019-07-24, просмотров: 429.