Цель работы: практическое изучение закона Гука.
Задача: определить практически модуль Юнга по растяжению стальной
проволоки.
Приборы и принадлежности: 1.Стальная проволока
2.Микроскоп отсчетный "МИР".
3.Микрометр.
4.Грузы.
Краткая теория
Сила характеризует действие одного тела на другое. В результате этого воздействия тело может прийти в движение или деформироваться. Деформацией твердого тела называется изменение взаимного расположения частиц тела, которое приводит к изменению формы и размеров тела и вызывает изменение сил взаимодействия между частицами, т. е. возникновение напряжений. Деформируемыми являются все вещества.
Деформация может быть следствием теплового расширения, воздействия электрических и магнитных полей, а также внешних механических сил.
В твердых телах деформация называется упругой, если она исчезает после снятия нагрузки, и пластической, если она после снятия нагрузки не исчезает.
Внутри деформированного тела возникает противодействующая сила, равная по величине деформирующей силе и называемая силой упругости. Силы упругости обусловлены взаимодействием между частицами (молекулами и атомами) тела и имеют электрическую природу.
Физическая величина, численно равная упругой силе 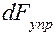 , приходящейся на единицу площади
, приходящейся на единицу площади 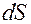 сечение тела, называется напряжением:
сечение тела, называется напряжением:
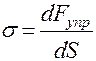
Английский физик Р. Гук экспериментально установил, что напряжение 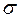 при упругих деформациях тела прямо пропорционально его относительной деформации
при упругих деформациях тела прямо пропорционально его относительной деформации 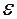 :
:
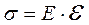 ,
,
где 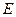 - модуль Юнга (модуль упругости), величина которого определяется свойствами материала, из которого изготовлено тело. Например,
- модуль Юнга (модуль упругости), величина которого определяется свойствами материала, из которого изготовлено тело. Например, 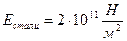 ;
; 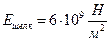 ;
; 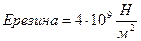 ;
; 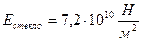 .
.
Относительная деформация равна отношению абсолютной деформации 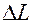 к начальной длине
к начальной длине 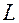 :
:
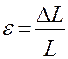 Рассмотрим упругую деформацию одностороннего растяжения проволоки
Рассмотрим упругую деформацию одностороннего растяжения проволоки
(рис. 1 ).
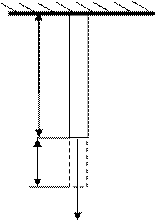 К нижнему концу закрепленной проволоки длиной
К нижнему концу закрепленной проволоки длиной 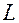 и площадью поперечного сечения
и площадью поперечного сечения 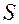
приложим силу 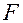 , под действием которой
, под действием которой
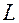 проволока получит абсолютное удлинение
проволока получит абсолютное удлинение 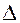
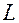
и в ней возникнет сила упругости 
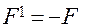 .
.
По закону Гука напряжение 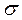 , возникшее в
, возникшее в
проволоке, прямо пропорционально относительной
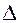 Ŀ деформации:
Ŀ деформации:
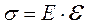 (1)
(1)
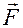 отсюда модуль Юнга равен: Е =
отсюда модуль Юнга равен: Е = 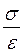
 (2) Рисунок 1- Деформация одностороннего растяжения проволоки
(2) Рисунок 1- Деформация одностороннего растяжения проволоки
Если положить, что 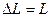 , т.е.
, т.е. 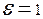 , то
, то 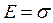 , т.е. модуль Юнга численно равен напряжению, возникающему в упруго деформированном теле, при относительной деформации, равной единице.
, т.е. модуль Юнга численно равен напряжению, возникающему в упруго деформированном теле, при относительной деформации, равной единице.
Заменив в формуле (2) напряжение и относительное удлинение по формулам 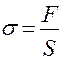 и
и 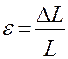 , получим:
, получим:
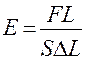 (3)
(3)
Площадь поперечного сечения проволоки 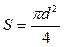 , (4)
, (4)
где  диаметр проволоки.
диаметр проволоки.
Подставив выражение (4) в (3) и учитывая, что 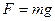 , получим расчетную формулу для модуля Юнга:
, получим расчетную формулу для модуля Юнга:
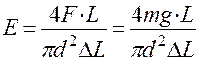 (5)
(5)
Порядок выполнения работы
1. Отметим на исследуемой проволоке какую-нибудь точку, для чего укрепим на ней кусочек тонкой проволоки.
2. Наведем на эту точку отсчетный микроскоп и заметим деление 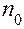 на шкале микроскопа, которое совпадает с указанной точкой. После этого кладем на чашку груз массой
на шкале микроскопа, которое совпадает с указанной точкой. После этого кладем на чашку груз массой 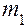 .
.
3. Определяем удлинение проволоки, вызванное нагрузкой 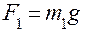 ,
,
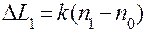
Здесь 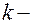 пересчетный коэффициент измерительного микроскопа, переводящий удлинение в делениях шкалы, видимой в окуляре, в миллиметры. Каждому значению длины тубуса микроскопа соответствует свое значение
пересчетный коэффициент измерительного микроскопа, переводящий удлинение в делениях шкалы, видимой в окуляре, в миллиметры. Каждому значению длины тубуса микроскопа соответствует свое значение 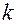 , которое указано в таблице на установке.
, которое указано в таблице на установке.
4. Вычисляем модуль Юнга по формуле (5), значение 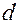 и
и 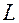 указаны на табличке возле установки.
указаны на табличке возле установки.
5. Опыты повторить с другими значениями масс 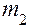 ,
, 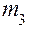 .
.
6. Результаты опытов занести в таблицу 1.
Таблица 1. Результаты измерений и расчетов.
| № опыта | 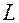
| 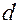
| 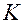
| 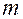
| 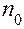
| 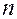
| 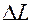
| 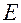
| 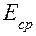
| 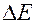
| 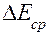
| 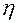
| 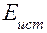
|
| 1 |
|
|
|
|
|
|
| ||||||
| 2 | |||||||||||||
| 3 |

Контрольные вопросы
1.Что называется деформацией, виды деформаций?
2.Какими величинами характеризуют деформацию растяжения (сжатия)?
3.Как читается закон Гука и для каких деформаций он справедлив?
4.Какой физический смысл модуля Юнга?
Литература [ 1,4,7 ]
ЛАБОРАТОРНАЯ РАБОТА № 4
Дата: 2019-07-24, просмотров: 402.