Пусть в результате измерения физической величины N получен ряд значений N 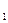 , N
, N 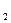 , N
, N 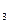 ,.…, N
,.…, N 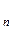 , где n - число отдельных измерений. Среднее арифметическое этих результатов, т.е.
, где n - число отдельных измерений. Среднее арифметическое этих результатов, т.е.
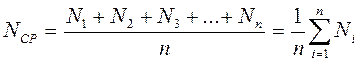 (1)
(1)
есть величина, называемая средним значением величины N, которая наиболее близка к истинному значению.
Отсюда следует, что каждое измерение должно быть повторено несколько раз.
Разности 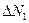 ,
, 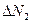 ,
, 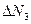 , …,
, …, 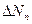 между средним значением измеряемой величины и значением
между средним значением измеряемой величины и значением 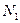 ,
, 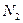 ,
, 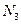 , …,
, …, 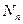 , полученным при отдельных измерениях, т.е.
, полученным при отдельных измерениях, т.е.
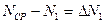
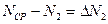
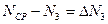
……………..
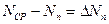
называются абсолютными ошибками или погрешностями отдельных измерений и могут быть положительными и отрицательными.
Для определения средней абсолютной погрешности результата берут среднее арифметическое абсолютных значений (модулей) отдельных ошибок:
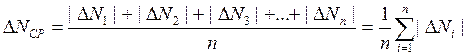
Отношения 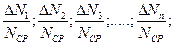 называются относительными погрешностями отдельных измерений.
называются относительными погрешностями отдельных измерений.
Отношение средней абсолютной погрешности результата 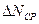 к его среднему значению
к его среднему значению 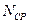 дает среднюю относительную погрешность результата измерений:
дает среднюю относительную погрешность результата измерений: 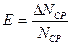
Относительные ошибки принято выражать в процентах
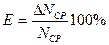
 Истинное значение
Истинное значение
N 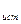 = N
= N 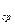
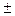
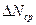



Не следует думать, что величина N ист имеет два значения N ср - 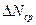 и N ср +
и N ср + 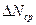 . N ист имеет только одно значение, а знак « + » или « – »
. N ист имеет только одно значение, а знак « + » или « – »  показывает , что истинное значение измеряемой величины находится в интервале
показывает , что истинное значение измеряемой величины находится в интервале
N ср - 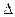 Nср
Nср 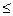 N ист
N ист 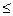 N ср +
N ср + 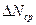 .
.
Теория вероятностей дает более точную формулу для вычисления абсолютной ошибки результата, устанавливая понятие так называемой наиболее вероятной ошибки результата 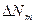 :
:
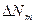 = ± 0, 6745
= ± 0, 6745 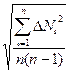
В этом случае окончательное значение измеряемой величины
N ист = N ср 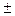
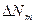
Если точность прибора такова, что при любом числе измерений получается одно и тоже число, лежащее где-то между делениями шкалы, то приведенный метод оценки погрешности неприменим. В этом случае измерение производится один раз и результат измерений записывается так:
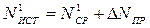 ,
,
где 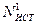 - искомый результат измерений;
- искомый результат измерений;
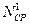 - средний результат, равный среднему арифметическому из двух значений, соответствующих соседним делениям шкалы, между которыми заключено остающееся неизвестным истинное значение измеряемой величины;
- средний результат, равный среднему арифметическому из двух значений, соответствующих соседним делениям шкалы, между которыми заключено остающееся неизвестным истинное значение измеряемой величины;
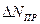 - предельная погрешность, равная половине цены деления шкалы прибора.
- предельная погрешность, равная половине цены деления шкалы прибора.
Часто в работах даются значения некоторых величин, измеренных заранее. В таких случаях абсолютную погрешность принимают равной ее предельной величине, т.е. равной половине единицы наименьшего разряда, представленного в числе. Например, если дана масса тела m=532,4 г , то 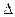 m=0.05 г, следовательно m
m=0.05 г, следовательно m 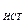 = 532.4 г
= 532.4 г 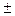 0.05 г. .
0.05 г. .
Дата: 2019-07-24, просмотров: 338.