1. Ознакомиться с установкой (рис.1). Убедиться в одинаковости длин нитей подвесок и при необходимости отрегулировать их.
2. Выполнить измерения. Для этого отвести шары на одинаковые углы ( 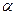 ) и заметить углы их наибольшего отклонения (
) и заметить углы их наибольшего отклонения ( 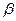 ) после первого удара.
) после первого удара.
3. Провести опыты с другими значениями 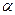 . Для каждого отклонения провести опыты по три раза.
. Для каждого отклонения провести опыты по три раза.
4. Выполнить расчеты 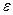 и
и 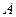 по формулам (12) и (13). Значения масс шаров и
по формулам (12) и (13). Значения масс шаров и
длины нитей берутся из таблички на установке.
5. Оценить погрешность измерения.
6. Результаты измерений и расчетов занести в таблицу отчета :
Таблица 1. Результаты измерений и расчетов
| № опыта |
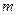
| R |
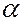
|
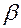
|
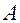
|
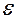
|
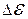
| 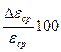 % %
|
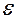 ист ист
|
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| Среднее значение |
Контрольные вопросы
1. Дать определения абсолютно упругого и абсолютно неупругого ударов.
2. Какие законы сохранения выполняются при этих ударах? Сформулировать
их.
3. Какой удар называется центральным?
4. Какими величинами оценивается степень "неупругости" удара?
5.Что называется коэффициентом восстановления и от чего он зависит?
6. По каким результатам проведенных вами исследований можно заключить, является ли удар шаров в лабораторной установке абсолютно упругим или абсолютно неупругим? Как вы назовете этот удар?
Литература [ 1,4,7 ]
 |
h
Рисунок 1 - Установка для изучения абсолютно упругого удара шаров
ЛАБОРАТОРНАЯ РАБОТА №2
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА
И СИЛЫ ТРЕНИЯ В ОПОРЕ
Цель работы: Закрепление теоретического материала по теме "Динамика вращательного движения твердого тела".
Задачи: Вычислить момент инерции махового колеса и силу трения в опоре.
Приборы и принадлежности: Прибор, состоящий из махового колеса, укрепленного на стене, масштабная линейка, штангенциркуль, секундомер, шнур с грузом.
Краткая теория
Твердое тело можно рассматривать как систему материальных точек, расстояние между которыми неизменно во время движения. Вращательным движением твердого тела называют такое движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения. Если тело может вращаться вокруг неподвижной оси, то изменение его движения зависит от действующего на тело момента силы. Моментом силы 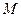 относительно неподвижной оси называется векторная физическая величина, численно равная произведению силы
относительно неподвижной оси называется векторная физическая величина, численно равная произведению силы 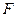 на её плечо
на её плечо 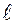 , т.е. кратчайшее расстояние от оси вращения до прямой, вдоль которой действует сила:
, т.е. кратчайшее расстояние от оси вращения до прямой, вдоль которой действует сила:
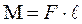 (1)
(1)
Вращательное движение твердого тела характеризуется угловой скоростью 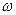 и угловым ускорением
и угловым ускорением 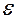 .
.
Угловой скоростью вращения называется вектор 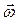 , численно равный первой производной от угла поворота
, численно равный первой производной от угла поворота 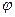 радиуса-вектора по времени и направленный вдоль оси вращения так, что из его конца вращение видно происходящим против часовой стрелки:
радиуса-вектора по времени и направленный вдоль оси вращения так, что из его конца вращение видно происходящим против часовой стрелки:
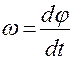 (2)
(2) 
Угловым ускорением называется вектор 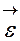 , равный первой производной от угловой скорости по времени:
, равный первой производной от угловой скорости по времени:
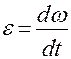 (3)
(3)
Моментом инерции материальной точки относительно оси вращения называют скалярную физическую величину, численно равную произведению массы этой точки на квадрат расстояния её до оси вращения:
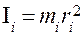

 (4)
(4)
Момент инерции твердого тела равен сумме моментов инерций материальных точек:
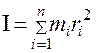 (5)
(5)
Зависимость углового ускорения 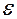 от момента
от момента 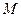
действующей на тело силы и момента инерции
 тела выражается вторым законом Ньютона
тела выражается вторым законом Ньютона

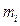 для вращательного движения (основным
для вращательного движения (основным
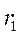 законом динамики вращательного движения):
законом динамики вращательного движения):
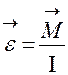 , (6)
, (6)

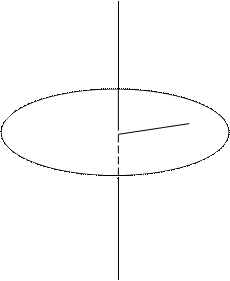
Рисунок 1 – Вращение твердого тела
Угловое ускорение 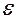 тела при его вращении вокруг неподвижной оси прямо пропорционально вращающему моменту М силы, действующей на тело, и обратно пропорционально моменту инерции І тела относительно этой оси.
тела при его вращении вокруг неподвижной оси прямо пропорционально вращающему моменту М силы, действующей на тело, и обратно пропорционально моменту инерции І тела относительно этой оси.
Если сопоставить законы поступательного и вращательного движений, легко сделать вывод, что момент инерции во вращательном движении выполняет ту же роль, что и масса в поступательном движении, так момент инерции характеризует инертность тела во вращательном движении.
Вращающееся тело обладает кинетической энергией:
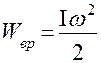 (7)
(7)
Момент инерции махового колеса и силу трения вала в опоре можно определить при помощи прибора, изображенного на рисунке 2.
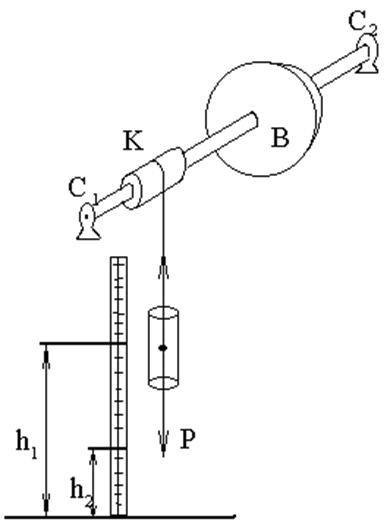
Рисунок 2 – Установка для изучения вращательного движения махового колеса
Прибор состоит из махового колеса B, укрепленного на валу. Вал установлен на шарикоподшипниках 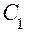 и
и 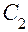 . Маховое колесо приводится во вращательное движение грузом Р. Груз Р на какой - то высоте
. Маховое колесо приводится во вращательное движение грузом Р. Груз Р на какой - то высоте 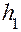 обладает потенциальной энергией
обладает потенциальной энергией 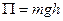
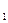 , где
, где 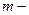 масса груза.
масса груза.
Если предоставить возможность грузу падать, то потенциальная энергия 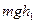 груза перейдет в кинетическую энергию
груза перейдет в кинетическую энергию 
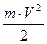 поступательного движения груза, кинетическую энергию вращательного движения
поступательного движения груза, кинетическую энергию вращательного движения 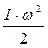 прибора и в работу
прибора и в работу 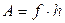 по преодолению силы трения
по преодолению силы трения 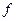 в опоре. По закону сохранения энергии
в опоре. По закону сохранения энергии
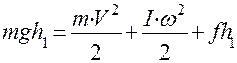 (8)
(8)
Движение груза - равноускоренное без начальной скорости, поэтому ускорение а и скорость 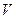 соответственно равны:
соответственно равны:
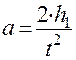 ;
; 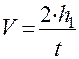 , (9)
, (9)
где t - время опускания груза с высоты h1.
Найдем угловую скорость махового колеса по формуле:
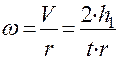 , (10)
, (10)
где 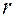 - радиус вала, на который намотана нить.
- радиус вала, на который намотана нить.
Сила трения 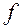 вычисляется следующим образом. После опускания груза колесо, вращаясь по инерции, поднимает груз на высоту
вычисляется следующим образом. После опускания груза колесо, вращаясь по инерции, поднимает груз на высоту 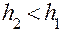 , и потенциальная энергия груза на высоте
, и потенциальная энергия груза на высоте 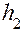 будет равна
будет равна 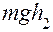 .
.
Уменьшение потенциальной энергии при подъеме груза равно работе по преодолению силы трения в опорах 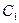 и
и 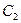 , т. е.
, т. е.
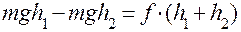 ,
,
отсюда
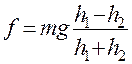 (11)
(11)
Подставляя в формулу (8) значения V, 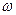 и
и 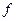 из (9), (10) и (11) получим окончательное выражение для вычисления момента инерции махового колеса:
из (9), (10) и (11) получим окончательное выражение для вычисления момента инерции махового колеса:
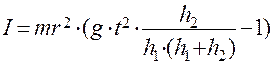 (12)
(12)
Порядок выполнения работы.
1. Наматывая на шкив шнур, поднять груз на высоту 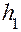 .
.
2. Отпустить груз и секундомером измерить время падения груза с высоты 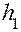 .
.
3. Определить высоту 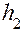 , на которую поднимается груз после опускания.
, на которую поднимается груз после опускания.
4. Измерить штангенциркулем радиус шкива 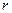 .
.
5. Повторить опыты при других значениях 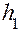 или массах
или массах 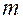 груза.
груза.
6. Вычислить момент инерции махового колеса и силу трения в опоре по формулам (12) и (11).
7. Полученные результаты занести в таблицу 1.
Таблица 1. Результаты измерений и расчетов
| № | 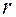
| 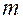
| 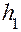
| 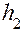
| 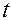
| 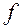
| 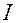
| 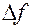
| 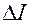
| 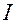 ист ист
|  ист ист
| Е, % | Е,% |
| 1 |
|
|
|
|
|
| |||||||
| 2 | |||||||||||||
| 3 | |||||||||||||
| сред знач. |
Контрольные вопросы
1. Что называют моментом инерции материальной точки, твердого тела относительно оси вращения? В каких единицах измеряется?
2. Что называется моментом силы относительно оси вращения?
Как записывается основной закон динамики для вращательного движения?
3. Чему равна кинетическая энергия вращающегося тела?
4. Как определить линейное ускорение груза и угловое ускорение колеса?
5. Какой закон положен в основу вывода расчетных формул?
Литература [ 1,4,7 ]
ЛАБОРАТОРНАЯ РАБОТА №3
Дата: 2019-07-24, просмотров: 447.