Установка (рис.2) представляет собой цилиндрическую стеклянную трубку (3) с глицерином или другой жидкостью, закрепленную на подставке. Для подогрева жидкости на трубку намотана спираль электронагревателя (4).
Температуру жидкости можно изменять, меняя ток в электронагревателе при помощи реостата R, а измерить – термометром (1). Шарики бросают через воронку (2), пройденный шариком путь (L) замечают по масштабной линейке (5).
Порядок выполнения работы
1. Измерить при помощи масштабной линейки расстояние 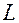 между двумя метками, нанесенными на стенку сосуда с жидкостью.
между двумя метками, нанесенными на стенку сосуда с жидкостью.
2. Измерить с помощью микрометра диаметр 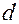 шарика.
шарика.
3. Опустить шарик в сосуд с исследуемой жидкостью и измерить секундомером время 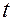 падения его между двумя метками.
падения его между двумя метками.
4. Занести в таблицу отчета значения всех величин (измеренных в опыте и табличных), необходимых для расчета коэффициента внутреннего трения.
5. По формуле (7) рассчитать коэффициент внутреннего трения жидкости.
6. Опыты повторить с 5 шариками.
7. С разрешения преподавателя включить цепь электронагревателя. Подогрев жидкость, повторить измерения, указанные в пунктах 2 и 3, и рассчитать коэффициент внутреннего трения при температурах ( 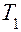 ,
, 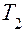 ), выше комнатной.
), выше комнатной.
8. Построить график зависимости 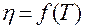 .
.
Таблица 1. Результаты измерений и расчетов
| № опыта | 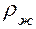
| 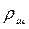
| 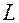
| 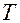
| 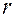
|  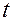 
| 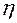
| 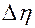
| 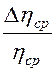
| 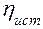
|
| 1 2 3 4 5 Сред. знач. |
 |
Рисунок 2 – Схема лабораторной установки
Контрольные вопросы
1. Какие явления относятся к явлениям переноса, и почему они так называются?
2. В чем состоит сущность явления внутреннего трения? Как записывается уравнение переноса для внутреннего трения (уравнение Ньютона)?
3. Дайте определение коэффициента внутреннего трения, от чего он зависит? В каких единицах измеряется?
4. Какие силы действуют на шарик, падающий в вязкой жидкости?
5. Запишите уравнение равномерного движения шарика в жидкости.
Литература [1,4,7 ]
| |
ЛАБОРАТОРНАЯ РАБОТА №7
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВНУТРЕННЕГО ТРЕНИЯ ГАЗА, СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА И ЭФФЕКТИВНОГО ДИАМЕТРА ЕГО МОЛЕКУЛ
Цель работы: практическое изучение одного из экспериментальных физических методов определения вязкости – метода Пуазейля.
Задачи работы:
1. Рассчитать коэффициент внутреннего трения (вязкость) воздуха, среднюю длину свободного пробега и эффективный диаметр молекул воздуха.
2. Исследовать зависимость коэффициента внутреннего трения газа от температуры.
Приборы и принадлежности: стеклянный баллон с краном в нижней части, капилляр, помещенный в электронагреватель, источник питания электронагревателя, секундомер, мерный и запасной стаканчики.
Теоретическое введение.
При движении слоев газа параллельно друг другу с различными по величине скоростями между ними возникают силы внутреннего трения (закон Ньютона)
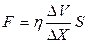 ,
,
где 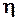 - коэффициент внутреннего трения газа (динамическая вязкость);
- коэффициент внутреннего трения газа (динамическая вязкость);
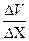 - градиент скорости; S – площадь соприкосновения слоев; Чтобы понять происхождение силы внутреннего трения, рассмотрим два соприкасающихся слоя газа, движущихся с различными скоростями
- градиент скорости; S – площадь соприкосновения слоев; Чтобы понять происхождение силы внутреннего трения, рассмотрим два соприкасающихся слоя газа, движущихся с различными скоростями 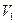 и
и 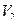 ( рис.1).
( рис.1).

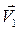
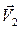
Рисунок -1 Поведение молекул в движущихся слоях газов
Каждая молекула газа участвует в двух движениях: хаотическом тепловом со средней скоростью 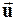 и упорядоченном движении со скоростью V. Вследствие хаотического теплового движения происходит непрерывный переход молекул из одного слоя в другой
и упорядоченном движении со скоростью V. Вследствие хаотического теплового движения происходит непрерывный переход молекул из одного слоя в другой
Попав в другой слой, молекула сталкивается с молекулами этого слоя, в результате чего она либо отдает избыток своего импульса другим молекулам (если она прилетела из слоя, движущегося с большей скоростью), либо увеличивает свой импульс за счет других молекул (если она прилетела из слоя, движущегося с меньшей скоростью). В итоге импульс более быстро движущегося слоя убывает, а более медленно движущегося возрастает. Слои ведут себя так, как если бы к первому слою (скорость которого больше) была приложена тормозящая его движение сила, а ко второму слою (скорость которого меньше) – такая же по величине ускоряющая сила.
Теория метода
Для измерения коэффициента динамической вязкости воздуха в данной работе используется метод Пуазейля (метод основан на определении скорости истечения жидкости или газа через капилляр). Если открыть кран К  , то вследствие вытекания воды из баллона давление воздуха будет уменьшаться и в него будет через капилляр засасываться воздух. Объем V газа, протекающего через капиллярную трубку радиуса r за время t, определяется по формуле Пуазейля:
, то вследствие вытекания воды из баллона давление воздуха будет уменьшаться и в него будет через капилляр засасываться воздух. Объем V газа, протекающего через капиллярную трубку радиуса r за время t, определяется по формуле Пуазейля:
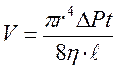 ,
,
где 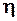 - коэффициент внутреннего трения или динамическая вязкость газа,
- коэффициент внутреннего трения или динамическая вязкость газа,
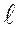 - длина капилляра,
- длина капилляра, 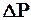 - разность давлений на его концах
- разность давлений на его концах
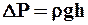
Здесь g – ускорение свободного падения, h – разность столбов жидкости в манометре, 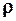 - плотность воды (1000
- плотность воды (1000 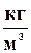 )
)
Из этой формулы получается выражение для 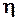 :
:
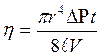 (1)
(1)
Здесь все величины доступны измерению, что позволяет экспериментально определять коэффициент внутреннего трения.
Коэффициент 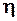 внутреннего трения связан со средней длиной
внутреннего трения связан со средней длиной 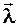 свободного пробега молекул, плотностью
свободного пробега молекул, плотностью 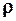 газа и средней арифметической скоростью
газа и средней арифметической скоростью 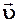 молекул газа соотношением:
молекул газа соотношением: 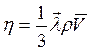 (2)
(2)
Средняя арифметическая скорость 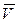 молекул определяется по формуле:
молекул определяется по формуле:
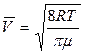 (3)
(3)
Плотность 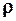 газа можно найти, воспользовавшись уравнением состояния газа:
газа можно найти, воспользовавшись уравнением состояния газа:
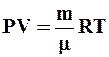 , отсюда
, отсюда 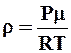 , (4)
, (4)
где P и T – давление и температура газа.
Решая совместно уравнения (2), (3) и (4), получим формулу для расчета средней длины 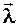 свободного пробега молекул газа:
свободного пробега молекул газа:
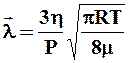 , (5)
, (5)
где R – универсальная газовая постоянная;
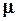 - молярная масса газа (для воздуха
- молярная масса газа (для воздуха 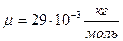 );
);
P – давление газа (в условиях данной задачи его можно считать равным 10 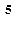 Па)
Па)
Из молекулярно-кинетической теории известно, что
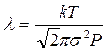
Отсюда найдем эффективный диаметр молекулы газа:
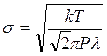 , (6)
, (6)
где k – постоянная Больцмана.
Порядок выполнения работы.
1. Открыть кран К  , подставив под него запасной стаканчик, и выждать пока установится стационарное течение (при этом разность уровней в манометре будет постоянной (рис.2).
, подставив под него запасной стаканчик, и выждать пока установится стационарное течение (при этом разность уровней в манометре будет постоянной (рис.2).
2. Измерить эту разность уровней h  .
.
3. Заменить запасной стаканчик мерным, включить секундомер и измерить время заполнения мерного стаканчика (50 или 100 см 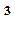 ).
).
4. Снова измерить разность уровней h 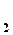 в манометре.По формулам (1), (5) и (6), используя программу, рассчитать коэффициент
в манометре.По формулам (1), (5) и (6), используя программу, рассчитать коэффициент 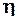 внутреннего трения, среднюю длину
внутреннего трения, среднюю длину 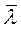 свободного пробега и эффективный диаметр
свободного пробега и эффективный диаметр 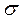 молекул газа.
молекул газа.
5. Опыт повторить 3 раза.
6. Результаты измерений и вычислений занести в таблицу (1) отчета.
7. Включив нагреватель (с разрешения преподавателя), повторить пункты
(1-5) при температурах, выше комнатной.
Таблица 1. Результаты измерений и расчетов
| № | Т | V | t | ℓ | r | h 
| h 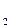
| 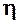
| 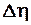
| 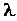
| 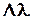
| σ | 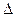 σ σ
|
Контрольные вопросы
1.Объясните механизм возникновения силы внутреннего трения в газе.
2.Запишите и поясните закон Ньютона.
3.В чем состоит метод Пуазейля, запишите и поясните формулу Пуазейля.
4.Дайте определения коэффициента внутреннего трения, средней длины свободного пробега и эффективного диаметра молекул газа?
5.От чего зависит коэффициент внутреннего трения газа?
Литература [1,4,7 ]

Рисунок 2 – Схема лабораторной установки
ЛАБОРАТОРНАЯ РАБОТА № 8
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ УДЕЛЬНЫХ ТЕПЛОЕМКОСТЕЙ ГАЗА 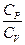 МЕТОДОМ АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ.
МЕТОДОМ АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ.
Приборы и принадлежности: стеклянный баллон, манометр, насос.
Цель работы: определение показателя адиабаты (коэффициента Пуассона) методом Клемана-Дезорма для воздуха.
Теория метода и описание установки.
Удельной теплоемкостью С газа называется скалярная физическая величина, численно равная количеству теплоты Q , которое необходимо сообщить единице массы газа, чтобы увеличить его температуру на 1 К:
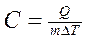 (1)
(1)
Величина теплоемкости газов зависит от условий нагревания. Выясним эту зависимость, воспользовавшись первым законом термодинамики, который гласит: количество теплоты Q , сообщенное системе, затрачивается на увеличение ее внутренней энергии 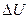 и на работу А, совершаемую системой против внешних сил
и на работу А, совершаемую системой против внешних сил
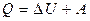 (2)
(2)
При изохорическом (V=const) нагревании газа 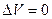 , следовательно, и А=0. Тогда все подводимое к газу тепло идет на увеличении его внутренней энергии:
, следовательно, и А=0. Тогда все подводимое к газу тепло идет на увеличении его внутренней энергии:
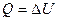
Из формулы (1) следует, что
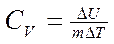 (3)
(3)
При изобарном (Р=const) нагревании газа тепло, сообщаемое газу идет и на увеличение внутренней энергии и на совершение газом работы против внешних сил:
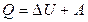 ,
,
поэтому 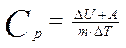 (4)
(4)
Сравнивая уравнения (3) и (4), получаем 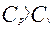 .
.
Отношение удельных теплоемкостей при постоянном давлении и при постоянном объеме 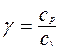 играет в термодинамике весьма важную роль. В частности оно входит в уравнение Пуассона, которое описывает адиабатическое расширение газа
играет в термодинамике весьма важную роль. В частности оно входит в уравнение Пуассона, которое описывает адиабатическое расширение газа
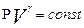 (5)
(5)
В данной работе прелагается один из самых простых методов определения 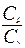 - метод Клемана и Дезорма. Адиабатическим процессом называется процесс, протекающий без теплообмена с окружающей средой, т.е. считается, что процесс передачи тепла системе от окружающей среды отсутствует.
- метод Клемана и Дезорма. Адиабатическим процессом называется процесс, протекающий без теплообмена с окружающей средой, т.е. считается, что процесс передачи тепла системе от окружающей среды отсутствует.
Экспериментальная установка состоит из стеклянного баллона А (рис. 1), соединенного с манометром В и с насосом.
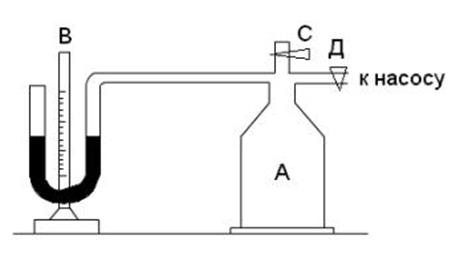
Рисунок 1- Схема экспериментальной установки
Если про помощи насоса накачать в баллон некоторое количество воздуха, то давление и температура воздуха внутри баллона повысятся. Вследствие теплообмена воздуха с окружающей средой через некоторое время температура воздуха, находящегося в баллоне, сравнятся с температурой внешней среды 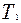 .
.
Давление, установившееся в баллоне
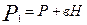 ,
,
где Р - атмосферное давление;
Н - разность уровней жидкости в манометре;
В - коэффициент перехода от разности уровней к давлению.
Таким образом, состояние воздуха внутри баллона, которое назовем 1 состоянием, характеризуется параметрами
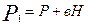 ;
; 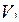 и
и 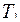
Если на короткое время открыть кран С, то воздух в баллоне будет расширяться. Этот процесс расширения можно считать адиабатическим. Давление в баллоне установится равным атмосферному Р, температура газа понизится до 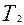 , а объем будет равен
, а объем будет равен 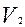 .
.
Следовательно, в конце адиабатического процесса, что назовем 2 состоянием, параметры состояния газа будут Р; 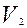 ,
, 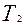 .
.
Применяя к 1 и 2 состояниям уравнение (5), получим:
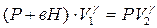 или
или 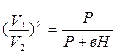 (6).
(6).
Охладившийся при адиабатическом расширении воздух в баллоне через некоторое время вследствие теплообмена нагреется до температуры внешней среды 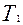 , давление возрастет до некоторой величины
, давление возрастет до некоторой величины
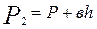 ,
,
где h- новая разность уровней в манометре.
Объем воздуха не изменится и будет равен 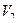 .
.
Это состояние воздуха, которое назовем 3 состоянием, характеризуется параметрами
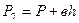 ;
; 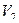 ;
; 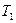
Так как в состояниях 1 и 3 воздух имеет одну и ту же температуру 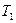 (процесс изотерический), то, применяя закон Бойля-Мариотта (PV=const), получим:
(процесс изотерический), то, применяя закон Бойля-Мариотта (PV=const), получим:
(P+вH) 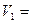 (P+вh)
(P+вh) 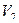
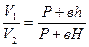
Возведем обе части уравнения в степень 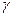 :
: 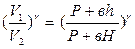 (7)
(7)
Решая совместно уравнения (6) и (7), получим: 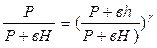
Логарифмируя это выражение и решая относительно 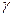 , находим
, находим
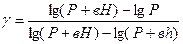
Так как давления Р, Р+вН и Р+вh мало отличаются друг от друга, то разности логарифмов можно принять пропорциональными разностям самих давлений и приближенно положить
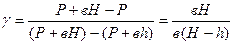
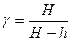 (8)
(8)

 Таким образом, экспериментальное определение
Таким образом, экспериментальное определение 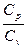 сводится к измерению H и h, то есть формула (8) является расчетной формулой для определения коэффициента
сводится к измерению H и h, то есть формула (8) является расчетной формулой для определения коэффициента 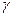 Пуассона
Пуассона
Порядок выполнения работы
1. Открыть кран Д, при закрытом кране С накачать воздух в баллон так, чтобы разность уровней жидкости в манометре составила 30-40 мм.
2. Закрыть кран Д и выждать 2-3 минуты, пока благодаря теплообмену температура в баллоне не станет равной комнатной, и уровни в коленах манометра перестанут изменяться.
3. Отсчитать разность уровней Н жидкости в коленах манометра.
4. Открыть кран С и в тот момент, когда уровни жидкости обоих коленах манометра сравняются, быстро закрыть кран С.
5. Выждать 2-3 минуты пока газ, охлажденный про адиабатическом расширении, нагреется до комнатной температуры 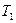 и отсчитать разность уровней h жидкости в коленах манометра.
и отсчитать разность уровней h жидкости в коленах манометра.
6. По формуле (8) вычислить значение 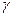 .
.
7. Опыт повторить 5-7 раз, меняя величину Н.
8. Все полученные результаты измерений занести в таблицу(1) отчета:
Таблица 1. Результаты измерений и расчетов
| № опыта | H | h | 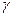
| 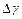
| 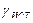
| E, % |
|
| ||||||
Контрольные вопросы
1. Что называется удельной теплоемкостью?
2. Запишите и сформулируйте I начало термодинамики
3. Почему 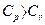 ?
?
4. Какой процесс называется адиабатическим? Запишите уравнение Пуассона.
5. Почему температура газа при адиабатном расширении уменьшается?
 P
P
 1(P
1(P 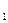 ,V
,V 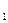 ,T
,T 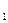 )
)
 3(P
3(P 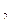 ,V
,V 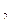 ,T
,T 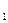 )
)

2(P,V 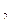 ,T
,T 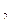 )
)
V
Рисунок 2 – Графики процессов, протекающих в работе
Литература [1,4,7 ]
ЛАБОРАТОРНАЯ РАБОТА № 9
Дата: 2019-07-24, просмотров: 381.